Контрольная по математике
.docВарианты заданий для типового расчета №1
по математике для специальностей «УП», «М»
Часть 1
Вариант №1
-
Вычислить определитель
-
Для матриц
и
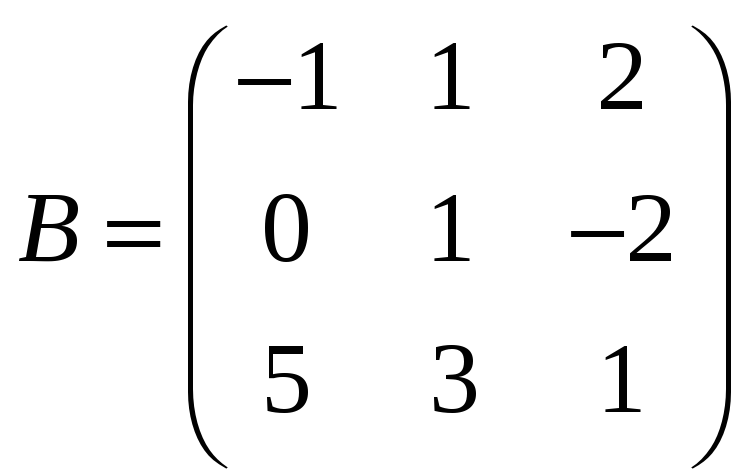вычислить матричный многочлен А2
– ВА
+ 3А. -
Вычислить обратную матрицу для матрицы
-
Найти ранг матрицы
-
Решить систему уравнений
Вариант №2
-
Вычислить определитель
-
Для матриц
и
вычислить матричный многочлен А2
– 2ВА
+ А. -
Вычислить обратную матрицу для матрицы
-
Найти ранг матрицы
-
Решить систему уравнений
Вариант №3
-
Вычислить определитель
-
Для матриц
и
вычислить матричный многочлен 2А2
+ ВА
+ 3А. -
Вычислить обратную матрицу для матрицы
-
Найти ранг матрицы
-
Решить систему уравнений
Вариант №4
-
Вычислить определитель
-
Для матриц
и
вычислить матричный многочлен В2
– ВА
+ 4А. -
Вычислить обратную матрицу для матрицы
-
Найти ранг матрицы
-
Решить систему уравнений
Вариант №5
-
Вычислить определитель
-
Для матриц
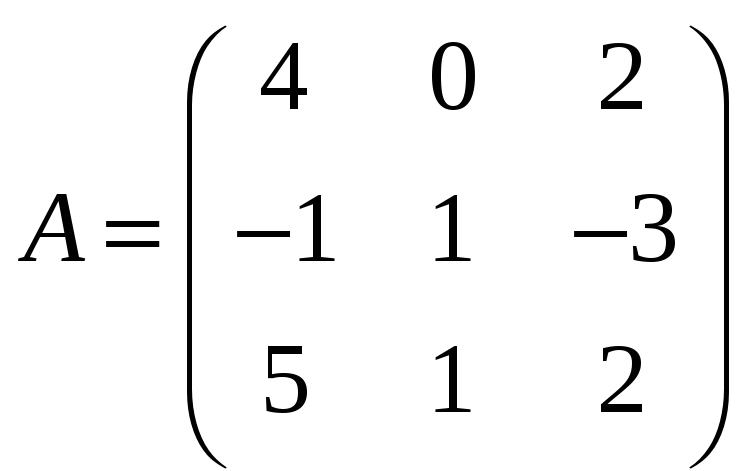и
вычислить матричный многочлен А2
+ ВА
+ 3В. -
Вычислить обратную матрицу для матрицы
-
Найти ранг матрицы
-
Решить систему уравнений
Вариант №6
-
Вычислить определитель
-
Для матриц
и
вычислить матричный многочлен А2
– ВА
+ 4В. -
Вычислить обратную матрицу для матрицы
-
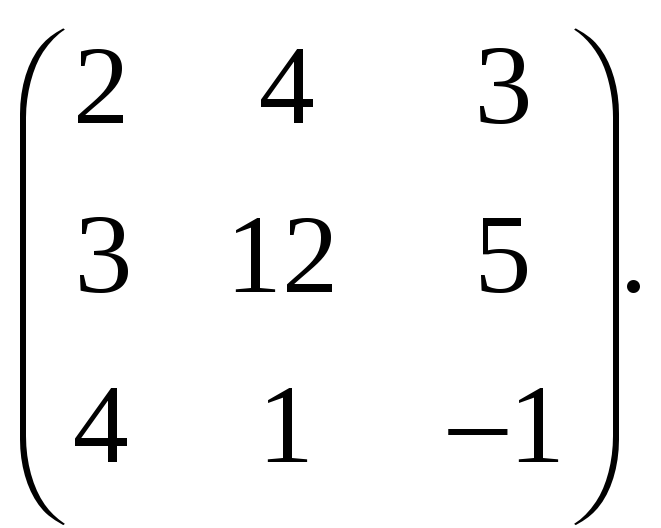
Найти ранг матрицы
-
Решить систему уравнений
Вариант №7
-
Вычислить определитель
-
Для матриц
и
вычислить матричный многочлен В2
– ВА
+ 3А. -
Вычислить обратную матрицу для матрицы
-
Найти ранг матрицы
-
Решить систему уравнений
Вариант №8
-
Вычислить определитель
-
Для матриц
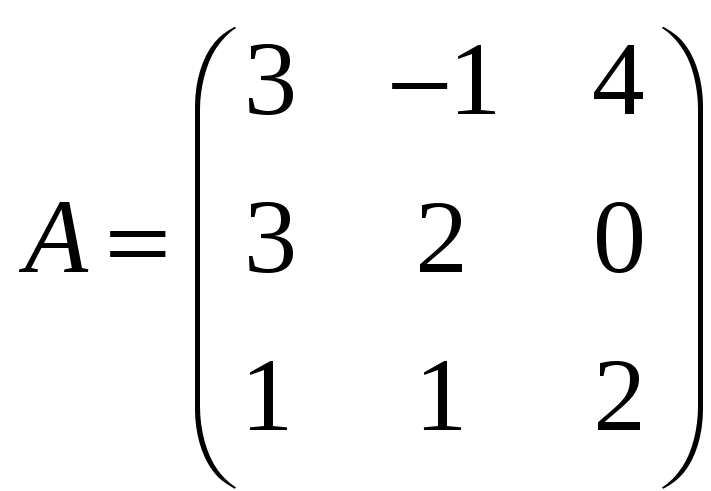и
вычислить матричный многочлен А2
+ 3ВА
+ 2В. -
Вычислить обратную матрицу для матрицы
-
Найти ранг матрицы
-
Решить систему уравнений
Вариант №9
-
Вычислить определитель
-
Для матриц
и
вычислить матричный многочлен А2
– ВА
+ 3А. -
Вычислить обратную матрицу для матрицы
-
Найти ранг матрицы
-
Решить систему уравнений
Вариант №10
-
Вычислить определитель
-
Для матриц
и
вычислить матричный многочлен В2
– ВА
+ 2А. -
Вычислить обратную матрицу для матрицы
-
Найти ранг матрицы
-
Решить систему уравнений
Часть 2
Задача № 1.
Написать разложение
вектора
по векторам
.
|
№ п/п |
|
|
|
|
|
1.1 |
(-2, 4, 7) |
(0, 1, 2) |
(1, 0, 1) |
(-1, 2, 4) |
|
1.2 |
(6, 12, -1) |
(1, 3, 0) |
(2, -1, 1) |
(0, -1, 2) |
|
1.3 |
(1, -4, 4) |
(2, 1, -1) |
(0, 3, 2) |
(1, -1, 1) |
|
1.4 |
(-9, 5, 5) |
(4, 1, 1) |
(2, 0, -3) |
(-1, 2, 1) |
|
1.5 |
(-5, -5, 5) |
(-2, 0, 1) |
(1, 3, -1) |
(0, 4, 1) |
|
1.6 |
(13, 2, 7) |
(5, 1, 0) |
(2, -1, 3) |
(1, 0, -1) |
|
1.7 |
(-19, -1, 7) |
(0, 1, 1) |
(-2, 0, 1) |
(3, 1, 0) |
|
1.8 |
(3, -3, 4) |
(1, 0, 2) |
(0, 1, 1) |
(2, -1, 4) |
|
1.9 |
(2, 2, -1) |
(3, 11, 0) |
(-1, 2, 1) |
(-1, 0, 2) |
|
1.10 |
(-1, 7, -4) |
(-1, 2, 1) |
(2, 0, 3) |
(1, 1, -1) |
Задача № 2.
Определить
коллинеарны ли векторы
, построенные на векторах
.
|
№ п/п |
|
|
|
|
|
2.1 |
(1, -2, 3) |
(3, 0, -1) |
|
|
|
2.2 |
(1, 0, -1) |
(-2, 3, 5) |
|
|
|
2.3 |
(-2, 4, 1) |
(1, -2, 7) |
|
|
|
2.4 |
(1, 2, -3) |
(2, -1, -1) |
|
|
|
2.5 |
(3, 5, 4) |
(5, 9, 7) |
|
|
|
2.6 |
(1, 4, -2) |
(1, 1, -1) |
|
|
|
2.7 |
(1, -2, 5) |
(3, -1, 0) |
|
|
|
2.8 |
(3, 4, -1) |
(2, -1, 1) |
|
|
|
2.9 |
(2, -3, -2) |
(1, 0, 5) |
|
|
|
2.10 |
(-1, 4, 2) |
(3, -2, 6) |
|
|
Задача № 3.
Найти косинус угла
между векторами
.
|
№ п/п |
|
|
|
|
3.1 |
(6, 5, 1) |
(0, 1, 2) |
(2, 1, 0) |
|
3.2 |
(5, 4, 2) |
(1, 2, 3) |
(3, 2, 1) |
|
3.3 |
(2, 0, 4) |
(1, 1, 1) |
(3, 2, 1) |
|
3.4 |
(1, 2, 3) |
(2, -1, 0) |
(3, 2, 1) |
|
3.5 |
(1, -1, 2) |
(5, -6, 2) |
(2, 3, -1) |
|
3.6 |
(3, -3, 1) |
(-3, -2, 0) |
(5, 0, 2) |
|
3.7 |
(4, 2, 1) |
(0, 4, 5) |
(1, 2, 7) |
|
3.8 |
(1, 0, 2) |
(2, 4, 3) |
(1, 7, 1) |
|
3.9 |
(5, -1, 3) |
(2, 0, 1) |
(3, 1, -1) |
|
3.10 |
(0, 8, 1) |
(2, 1, 1) |
(-1, 4, 5) |
Задача № 4.
Определить
компланарны ли вектора
,
и
.
|
№ п/п |
|
|
|
|
4.1 |
(2, 3,1) |
(-1, 0, -1) |
(2, 2, 2) |
|
4.2 |
(3, 2, 1) |
(2, 3, 4) |
(3, 1, -1) |
|
4.3 |
(1, 5, 2) |
(-1, 1, -1) |
(1, 1, 1) |
|
4.4 |
(1, -1, -3) |
(3, 2, 1) |
(2, 3, 4) |
|
4.5 |
(3, 3, 1) |
(1, -2, 1) |
(1, 1, 1) |
|
4.6 |
(3, 1, -1) |
(-2, -1, 0) |
(5, 2, -1) |
|
4.7 |
(4, 3, 1) |
(1, -2, 1) |
(2, 2, 2) |
|
4.8 |
(4, 3, 1) |
(6, 7, 4) |
(2, 0, -1) |
|
4.9 |
(3, 2, 1) |
(1, -3, -7) |
(1, 2, 3) |
|
4.10 |
(3, 7, 2) |
(-2, 0, -1) |
(2, 2, 1) |
Задача № 5.
Вычислить объем
пирамиды с вершинами в точках
,
,
и
и ее высоту, опущенную из вершины
на грань
.
|
№ п/п |
|
|
|
|
|
5.1 |
(0, 1, 2) |
(2, 1, 7) |
(2, 7, 4) |
(0, 0, 4) |
|
5.2 |
(1, 2, 3) |
(2, 8, -4) |
(0, 5, 4) |
(2, 9, 4) |
|
5.3 |
(1, 1, 1) |
(2, 4, -2) |
(2, 0, 2) |
(0, 1, -1) |
|
5.4 |
(1, -1, 1) |
(0, 2, 3) |
(1, -1, 0) |
(0, 2, 2) |
|
5.5 |
(2, 1, 3) |
(4, -2, 0) |
(1, 3, -3) |
(7, 5, 2) |
|
5.6 |
(-2, 0, 4) |
(1, 3, -1) |
(4, -1, 3) |
(2, 7, 3) |
|
5.7 |
(1, 2, 3) |
(0, 0, 0) |
(1, 4, 3) |
(1, 8, -1) |
|
5.8 |
(-1, 2, 0) |
(1, 0, 3) |
(0, 2, 2) |
(1, 8, 3) |
|
5.9 |
(2, -1, 1) |
(3, 3, 2) |
(2, 1, 0) |
(4, 1, -3) |
|
5.10 |
(2, 1, -1) |
(-3, 1, 2) |
(0, 1, 2) |
(-1, 8, 3) |
Часть 3.
Аналитическая геометрия на плоскости
Заданы вершины
треугольника
-
Написать уравнения всех сторон треугольника.
-
Задать множество внутренних точек треугольника.
-
Написать уравнение высоты, проведённой из вершины А.
-
Написать уравнение медианы, проведённой из вершины В.
-
Написать уравнение биссектрисы, угла С.
-
Найти угол между медианой и биссектрисой из п.п.4,5
-
Найти центр и радиус описанной окружности.
-
Найти длину высоты, опущенной из вершины В.
-
Найти площадь треугольника АВС
-
Найти проекцию точки А на сторону АС
-
Записать уравнение стороны АВ в форме уравнения прямой в отрезках.
-
Записать уравнение прямой ВС в форме уравнения прямой с угловым коэффициентом.
-
Записать уравнение прямой АС в форме нормального уравнения
-
Записать уравнение прямой, проходящей через т. N(10,10) параллельно стороне АВ.
-
Записать уравнение прямой, проходящей через т.М (-10,-10) перпендикулярно стороне ВС.
|
№ |
А |
В |
С |
|||
|
x1 |
y1 |
x2 |
y2 |
x3 |
y3 |
|
|
1 |
2 |
3 |
-1 |
2 |
7 |
-1 |
|
2 |
3 |
4 |
-2 |
1 |
7 |
-2 |
|
3 |
3 |
5 |
-1 |
3 |
7 |
-3 |
|
4 |
4 |
3 |
-2 |
3 |
7 |
-4 |
|
5 |
5 |
1 |
-3 |
2 |
7 |
-5 |
|
6 |
2 |
5 |
-3 |
1 |
7 |
-6 |
|
7 |
6 |
1 |
-1 |
4 |
6 |
-7 |
|
8 |
5 |
3 |
-2 |
4 |
5 |
-7 |
|
9 |
6 |
2 |
-3 |
4 |
4 |
-7 |
|
10 |
2 |
6 |
-4 |
3 |
3 |
-7 |