Лабораторная работа № .....Графы
1. Основные понятия
В теории графов (graphs) рассматриваются конфигурации из точек – вершин (vertices) и линий – рёбер (edges), соединяющих некоторые из этих точек.
Графом
называется совокупность двух множеств:
множества вершин V
и множества рёбер Е.
Множество рёбер можно рассматривать
как множество
![]() пар вершин вида
пар вершин вида
![]() ,
где
,
где
![]() V.
Пара
V.
Пара
![]() соответствует ребру, идущему из вершины
соответствует ребру, идущему из вершины
![]() в вершину
в вершину
![]() .
.
Если
порядок вершин является существенным,
то есть ребра
![]() и
и
![]() необходимо различать, то граф называется
ориентированным
и соответствующие рёбра называются
дугами (arcs).
Они изображаются линиями со стрелками.
В этом случае вершина
необходимо различать, то граф называется
ориентированным
и соответствующие рёбра называются
дугами (arcs).
Они изображаются линиями со стрелками.
В этом случае вершина
![]() ,
стоящая в паре
,
стоящая в паре
![]() на первом месте, называется начальной
(tail
– хвост), а другая вершина
на первом месте, называется начальной
(tail
– хвост), а другая вершина
![]() — конечной
(head
– голова). В этом случае ребро
— конечной
(head
– голова). В этом случае ребро
![]() характеризуют как
исходящее
из вершины
характеризуют как
исходящее
из вершины
![]() и входящее
в вершину
и входящее
в вершину
![]() .
Ориентированный граф сокращённо
называется орграфом,
по-английски digraph
(dimension
graph,
dimension
– направление).
.
Ориентированный граф сокращённо
называется орграфом,
по-английски digraph
(dimension
graph,
dimension
– направление).
Например, ориентированным графом может выражаться отношение потребления одними заводами продукции других заводов.
Пример. На рис. 1 изображены орграфы с тремя, четырьмя и шестью вершинами.
|
|
|
Рис. 1 |
Если
порядок упоминания вершин любого ребра
![]() несущественен, то граф называется
неориентированным.
несущественен, то граф называется
неориентированным.
Например, неориентированным графом может выражаться отношение знакомства друг с другом некоторых студентов из числа собравшихся в аудитории. В этом случае неориентированные ребра графа изображаются линиями без указания направления, то есть без стрелок.
Пример. На рис. 2 изображены неориентированные графы с четырьмя, пятью и семью вершинами.
|
|
|
Рис. 2 |
Среди
рёбер графа могут встречаться петли
вида
![]() ,
соединяющие вершину
,
соединяющие вершину
![]() с нею же самой. На рис. 3 изображен
ориентированный граф с петлями в вершинах
с нею же самой. На рис. 3 изображен
ориентированный граф с петлями в вершинах
![]() и
и
![]() .
.
|
|
|
Рис. 3 |
2. Матрица смежности
Матрицей
смежности
(adjacency
matrix) ориентированного
графа с
множеством вершин
![]() называется квадратная матрица
называется квадратная матрица
![]() размера
размера
![]() ,
состоящая из нулей и единиц. При этом
,
состоящая из нулей и единиц. При этом
![]() ,
если граф содержит ребро, исходящее из
вершины
,
если граф содержит ребро, исходящее из
вершины
![]() и входящее в вершину
и входящее в вершину
![]() ;
если такого ребра нет, то
;
если такого ребра нет, то
![]() .
.
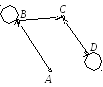
Примеры. 1. Матрица смежности ориентированного графа, изображённого на рис. 4, имеет вид
|
|
A |
B |
C |
D |
|
A |
1 |
1 |
1 |
0 |
|
B |
0 |
0 |
0 |
1 |
|
C |
0 |
0 |
0 |
0 |
|
D |
1 |
0 |
0 |
0 |
|
|
|
Рис. 4 |
2. Ориентированный граф, заданный матрицей смежности
|
|
A |
B |
C |
D |
E |
|
A |
0 |
1 |
1 |
0 |
0 |
|
B |
0 |
0 |
1 |
1 |
1 |
|
C |
0 |
0 |
0 |
0 |
0 |
|
D |
0 |
0 |
0 |
1 |
0 |
|
E |
0 |
0 |
1 |
0 |
0 |
имеет вид, изображённый на рис. 5.
|
|
|
Рис. 5 |
Аналогично
матрицей смежности
неориентированного
графа
с множеством вершин
![]() называется матрица
называется матрица
![]() ,
состоящая из нулей и единиц. При этом
,
состоящая из нулей и единиц. При этом
![]() ,
если граф содержит ребро, соединяющее
вершины
,
если граф содержит ребро, соединяющее
вершины
![]() и
и
![]() ;
если такого ребра нет, то
;
если такого ребра нет, то
![]() .
.
Матрица смежности неориентированного графа является симметрической (элементы, расположенные симметрично относительно главной диагонали, совпадают).
Примеры. 1. Матрица смежности неориентированного графа, изображённого на рис. 6, имеет вид
|
|
A |
B |
C |
D |
E |
F |
G |
H |
K |
|
A |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
B |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
C |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
D |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
E |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
F |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
G |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
H |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
K |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
Рис. 6 |
2. Неориентированный граф, заданный матрицей смежности
|
|
A |
B |
C |
D |
E |
|
A |
0 |
1 |
1 |
1 |
1 |
|
B |
1 |
0 |
0 |
1 |
1 |
|
C |
1 |
0 |
0 |
0 |
0 |
|
D |
1 |
1 |
0 |
0 |
0 |
|
E |
1 |
1 |
0 |
0 |
0 |
имеет вид, изображённый на рис. 7.
|
|
|
Рис. 7 |