
Labs_EF-16 / Лаб7_Фёдоров
.rtf
-
Подключили пакет LinearAlgebra
![]()

-
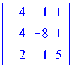
Задали матрицу A и вектор b
![]()
![]()
![]()
-
Найти обратную матрицу для A
![]()

-
Найти решение уравнения
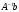
![]()
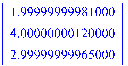
-
Найти решение с помощью команды LinearSolve
![]()
![]()
-
Записали два уравнения.
![]()
![]()
![]()
![]()
-
Выразили из первого уравнения
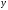 (обозначили
F
через
(обозначили
F
через
 ),
а из второго
),
а из второго
 (обозначили G
через
(обозначили G
через
 )
)
![]()
![]()
![]()
![]()
-
Построили графики этих функций, используя функцию implicitplot пакета plots
![]()

![]()
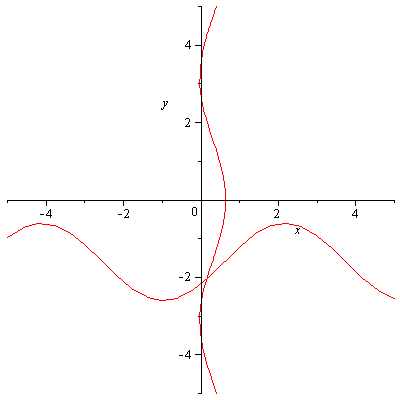
-
Выбрали начальное приближение
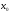 и
и
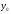 из графика, обозначили x[0]
и y[0]
из графика, обозначили x[0]
и y[0]
![]()
![]()
![]()
![]()
-
Задали погрешносли вычислений

![]()
![]()
-
Найти решение путем итераций по формуле
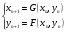 .
Т.е. написали цикл, выход из которого
осуществляется когда
.
Т.е. написали цикл, выход из которого
осуществляется когда
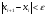 и
и
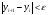 .
.
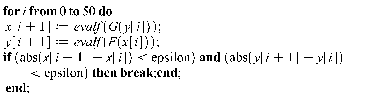
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Проверили полученное решение командой solve.
![]()
![]()
![]()
![]()
![]()
![]()
-
Записали два уравнения так, чтобы в правой части был ноль, обозначили F, а из второго обозначили G (через
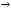 ).
).
![]()
![]()
![]()
![]()
-
Построили графики этих функций, используя функцию implicitplot пакета plots
![]()

![]()
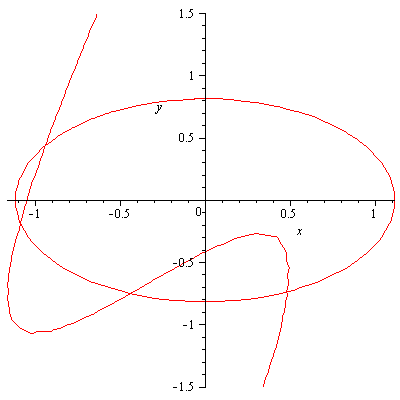
-
Выбрали начальное приближение
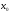 и
и
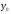 из графика, обозначили x[0]
и y[0]
из графика, обозначили x[0]
и y[0]
![]()
![]()
![]()
![]()
-
Задали погрешносли вычислений

![]()
![]()
-
Найти частные производные
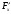 ,
,
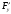 ,
,
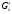 и
и
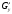 и сделали их функциями своих аргументов,
для этого можно использовали команду
unapply(функция, от_чего_зависит)
и сделали их функциями своих аргументов,
для этого можно использовали команду
unapply(функция, от_чего_зависит)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Найти решение путем итераций по формуле
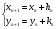 где:
где:
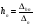 ,
,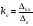
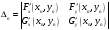
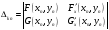
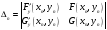 Все
эти формулы пишутся в цикле, выход из
которого осуществляется когда
Все
эти формулы пишутся в цикле, выход из
которого осуществляется когда
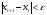 и
и
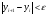 .
Определители находятся с помощью
функции Determinant
пакета LinearAlgebra.
.
Определители находятся с помощью
функции Determinant
пакета LinearAlgebra.
![]()
![]()
![]()
![]()
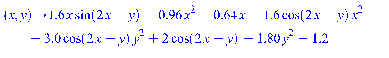
![]()
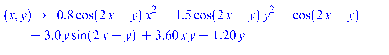
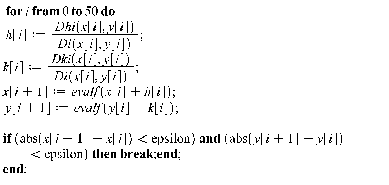
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
Проверили полученное решение командой solve.
![]()
![]()
![]()
