№146.11.Барщевский

352

ленаправленных элементов на каждом уровне и K0 = K1 элементов объекта управления (уровень h = 0).

Проектирование задач целенаправленной системы управления производством заключается в выборе такого пути μ* M на графе G, что [2]

Эффект проектирования (Пн.2) определяется:

1)выбранными дугами маршрута μ, определяющими “затратную” часть эффекта при проектировании;

2)принятыми узлами маршрута μ, т.е. выбранными при проектировании моделями, используемыми при эксплуатации и характеризующими “доходную” часть эффекта.

Вобщем случае задача (Пн.2) нелинейна и требует (при проектировании) учета функционально-целевых отношений, а процесс ее решения носит комбинаторный, эвристический характер.

Вто же время при прочих равных условиях проектирования более высокий эффект получается при максимизации эффекта в узлах маршрута

Ф= Фф + Фр Æ max,

где Фф и Фр – эффекты от эксплуатации моделей процедур функционирования и адаптации. В соответствии с поставленными задачами

Фs = Фs(Фs1, Фs2, Фs3) Æ max,

где s = ф или s = р; Ф1 ,Ф2, Ф3 – составляющие эффекта, связанные с выбором структурных связей, синтезом процессов планирования и управления.

В свою очередь

где S – связи между элементами системы; ε – вектор отклонения вектор-выхода от вектор-плана p; u – вектор управления; Фs1(S) = Фs1(Sп, Sу); Sп, Sу – структуры процессов планирования и управления. Иными словами, выделены бизнеспроцессы планирования и управления.

Заметим, что более простая структура планирования повторяется в виде составной части в более сложной структуре управления. В связи с этим построение структур Sп и Sу можно объединить и вести речь о создании структуры (топологии) S, подразумевая прежде всего Sу.

Для отображения бизнес-процессов используют систему моделей стандарта IDEF, предложенного в концепции ICAM и воспринятую в концепции

353

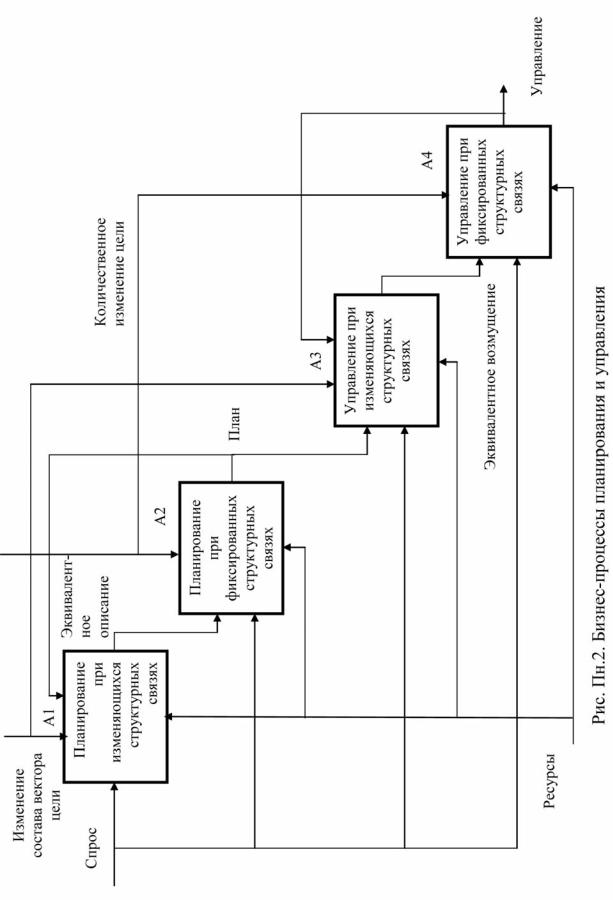
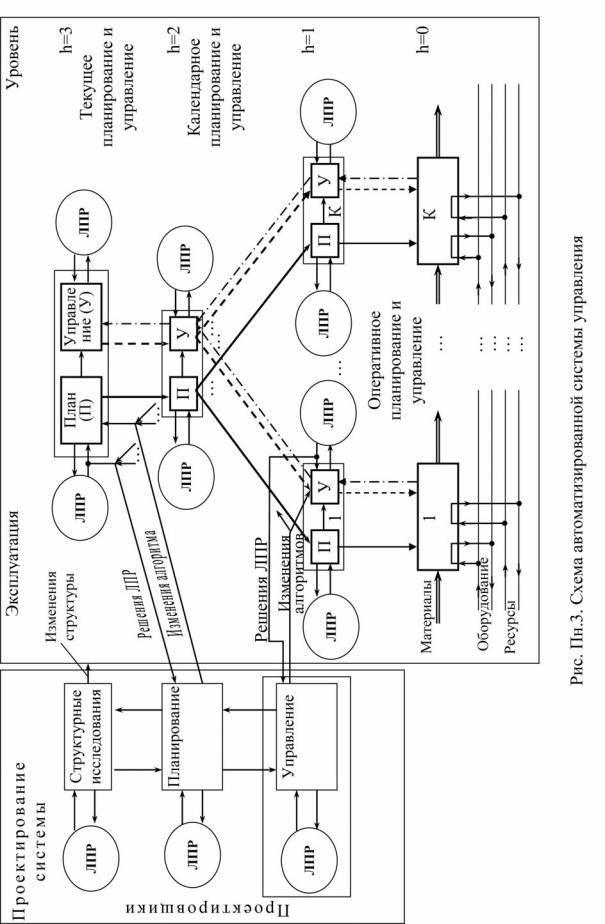
ESPRIT. Обычно применяют модели IDEF0 для отображения функциональных связей и IDEF3 – для представления информационных потоков. Модель IDEF0 может иметь иерархическую структуру. Вместо модели IDEF3 [2] часто – в силу большей наглядности – применяются диаграммы потоков данных (Data Flow Diagram – DF-диаграмма). Модель IDEF0 рассматриваемых в данной работе бизнес-процессов планирования и управления показана на рис. Пн.2. Иерархическую детализацию этой модели при системном ее представлении удобнее представить в виде рис. Пн.3.

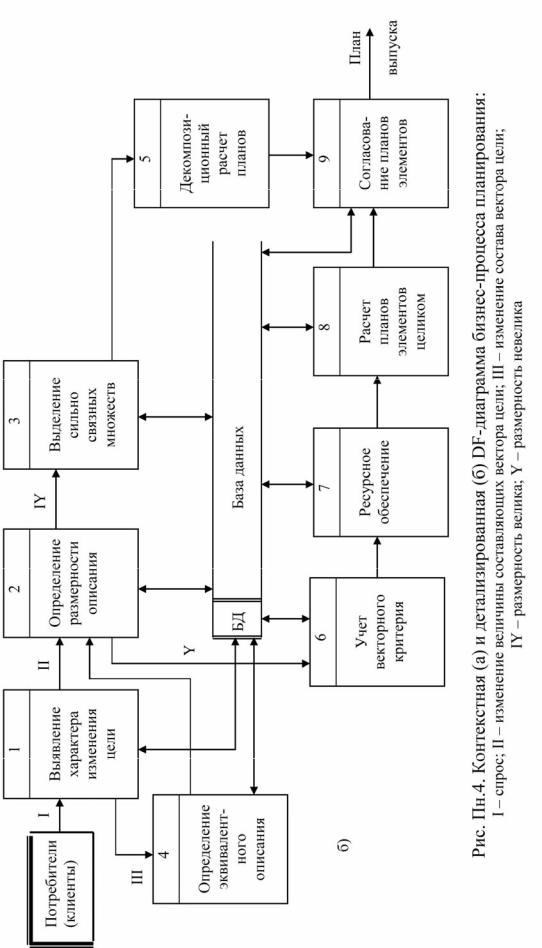
Таким образом, речь идет о построении моделей, обеспечивающих условия (Пн.3) и учитывающих ограничения (статические – на ресурсы и динамические – на процессы в объекте управления), и порядок (технологию) моделирования (рис. Пн.4), для отражения которых используют DF-диаграммы.

DF—диаграмма для процесса планирования показана на рис. Пн.4. На ее основе строится набор ST-диаграмм (State Transaction Diagram), отображающих отдельные бизнес-функции для последующей их компьютерной реализации. В то же время системное представление всего сложного процесса управления более наглядно в виде схемы, показанной на рис. Пн.5.

Рассмотренные предпосылки позволили сформировать обобщенную модель (ОМ) системы, которую удобнее представить не моделью IDEF0, а моделью М(1) с нелинейными – в общем виде – операторами.

В силу сложности описания и анализа структуры с произвольным числом уровней с содержательной и методической точек зрения удобнее эту структуру представить в виде “троек” уровней управляющей части совместно со структурой объекта управления (h = 0) на нижнем, технологическом уровне. При этом на верхнем h = 3 и среднем h = 2 уровнях K3 = K2 = 1, на нижнем (h =1) уровне число элементов K1 > 1, а K0 = K1.

Элементарный интервал времени на уровнях h = 0, 1, 2 составляет [ti] = [t] = const, i = 1, m; на уровне h = 3 элементарный интервал [T] = m*[t] или [t] =

μ*[T], μ = 1/m. На уровне h = 2 увеличивается – по сравнению с уровнем h = 1 – размерность по координатам, а на уровне h = 3 осуществляется агрегация по времени и координатам по сравнению с уровнем h = 2.

Целенаправленность элементов kh Kh, h = 1, 3 проявляется в виде интереса (целевой функции Фkh). Полагаем при этом, что цель Ф системы в общем случае совпадает с целью Ф3 элемента K3, с которой должны быть согласованы цели других элементов kh, h ≠ 3.

Такая система – в терминах АСУП – совокупность взаимодействующих подсистем технико-экономического планирования и оперативного управления основным производством, при этом предполагается, что маркетинговые исследования проведены и их результаты известны.

ОМ, как общая постановка задачи для решаемой автором проблемы, имеет вид следующих связанных формализованных задач для процедур функционирования и адаптации.

354

355

356

357

Начало

Идентификация

Фиксированная

структура

Планирование

t = 1

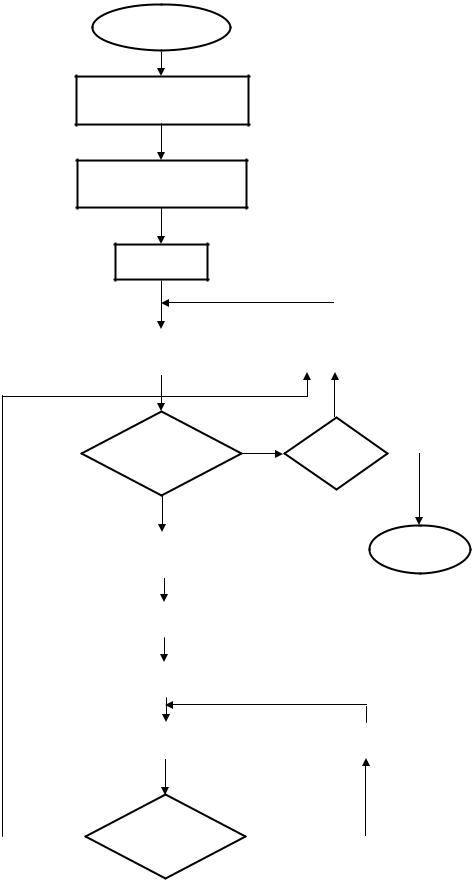
Рис. Пн.5. Обобщенная технология моделирования:

А – цель меняется; t’, T’ – характеристики «структурного» переходного процесса

358

ПРОЦЕДУРА ФУНКЦИОНИРОВАНИЯ.

Ф1.1. Построение топологии (структуры): выбрать элементы Э выражения (рис. 8.1)

Mluhl(1) = {Эmh+2(u, th+2) * Эkh+1(u, th+1) *

* Эlh(u, th) * Эlh(y, th) * Эjh(y, th)}, l = 1, K, h = 0, θ, (Пн.7)

таким образом, чтобы

где Эkh+1(u, th+1), Эlh(u, th ), Эlh(y, th ) – k-е и l-е элементы соответствующих уровней управляющей части и объекта управления; u, y – векторы управления и выхода; th – отсчет времени на уровне h; * – оператор замыкания, учитывающий обратные связи; Kh – количество элементов на уровне h; h = 1, θ; θ – количество

уровней системы; S – связи между элементами Э; l C(k), C(k) = {l: ГЭkh+1 = Эlh,

|C(k)| = Nl, k = 1, Kh+1, l = 1, Kh; j C(l), C(l) = {j: ΓЭjh = Эlh }, |C(l)| = Nj, j = 1, Nj; C(r) = {r: Эrh = Г-1Эkh+1 }, |C(r)| = Nr; Г – прямая связь двух смежных элементов.

Из выражения (Пн.7) видно, что такая структура исчерпывает возможные изменения масштабов по координатам и по времени на границах уровней и определяет простейшую (минимальную) базовую трехуровневую (θ = 3) топологию. При θ > 3 базовая структура может “скользить” по структуре реальной системы.

Заметим, что в системе управления производством топология элемента Эlh(y, th) должна включать топологии взаимодействующих потоков ресурсов (материальных, трудовых, оборудования, финансовых, информационных). Однако все потоки ресурсов, кроме материальных, фактически локализуются в пределах этого элемента, в силу чего топология Эlh(y, th) * Эjh(y, th) фактически есть топология материальных ресурсов.

Отметим, что в известных публикациях используются частные структуры

(Пн.7)

Mluhl(1) = { Эkh+1(u, th+1) * Эlh(u, th) * Эlh(y, th) * Эjh(y, th)},

и

Mluhl(1) = {Эkh+1(u, th+1) * Эlh(u, th) * Эlh(y, th),

т.е. при отсутствии горизонтальных связей в объекте управления.

Ф1.2. Идентификация (определение) структуры: определить вид структуры (Пн.7) для действующей многоуровневой системы в соответствии с выбранной целью Ц исследования.

Описание Ф1.1 – трудоемкое построение структуры для нового предприятия, требующее специальной технологии. В дальнейшем под Ф1 будет пониматься описание Ф1.2.

359

Ф2. Процесс планирования: определить оптимальный план Plh(th), исходя из ограничений

MПlPh(1) = П{Pmh+2(th+2), Pkh+1(th+1), xl(th), blh(th), σh,

Flh, Plh(th), Pjh(th)} (Пн.9)

и целевой функции

где Plh(th) – вектор плана; xlh, blh – векторы входа и запасов ресурсов; σlh – матрица норм расходов; m, k – определяются как в (1.7) и (1.8); П – оператор планирования; Flh – критерий.

Структура планирования в общем случае имеет вид (рис. 1.4):

Mlph(1) = Эmh+2(P, th+2) Эkh+1(P, th+1) {Эlh(P, th) Эjh(P, th)}, (Пн.11)

где – оператор прямой связи. Однако и здесь чаще обращаются к более простым структурам

Mlph(1) = Эkh+1(P, th+1) {Эlh(P, th) Эjh(P, th)}

и

Mlph(1) = Эkh+1(P, th+1) Эlh(P, th).

Топология управления (1.7) действительно, как отмечалось ранее, полностью содержит топологию планирования (1.11).

Если в подсистеме используется диалоговый режим, то выражения (Пн.9) и (Пн.10) получают вид

где Plh, Prlh, P1ЛПРh – векторы машинного решения-совета, приоритета и решения ЛПР.

Расчет плана для системы управления производством ведется поочередно по уровням, начиная с верхнего (h = 3). В таком случае иерархия расчета совпадает с иерархией процесса планирования.

Если задача планирования для элемента kh структуры имеет высокую размерность, ее следует решать по частям. В этом случае в иерархии расчета появляется дополнительный уровень. Деление задачи на части соответствует в топологии операции, называемой гомологией.

Целенаправленная система управления производством (выражения (Пн.9), (Пн.10)) имеет потребность в вертикальном и горизонтальном согласо-

360

вании интересов элементов Flh в процессе планирования и управления. Полагаем, что интересы системы Ф2ф и верхнего уровня F1θ совпадают.

Вертикальное согласование в формальном виде можно представить следующим образом (два случая):

1. Пусть задача (Пн.9), (Пн.10) имеет решение Plh-1(th) для топологии

{Эkh+1(P, th+1) * Эlh(P, th)} при замене h на (h —1) и решения Plh(th) , {l = 1, N} для топологии {Эkh+1(P, th+1) * Эlh(P, th) * Эjh(P, th)}. Тогда компромиссное решение

где Fl' – целевая функция компромисса.

Заметим, что в этом случае меняется масштаб по координатам на границах уровней, тогда как масштаб по времени сохраняется.

2. Пусть задача (1.9), (1.10) имеет решение Pkh(th) для топологии Эkh+1(P,

th+1) Эlh(P, th) и решение Pkh-1(th-1) = {Pklh-1(th-1), l = 1, Nl} для топологии Эkh+1(P, th+1) {Эlh(P, th) Эjh(P, th)} при замене h на (h -1). Компромиссное решение

P'kh(th) = Arg extr Fl'

Fk' = Fk'{Pkh(th), Pkh-1(th-1), P'kh(th)}, (Пн.14)

где Fl' – целевая функция компромисса. В этом случае на границе уровней меняются масштабы как по координатам, так и по времени.

Пусть при горизонтальном согласовании задача (1.9), (1.10) для топологии Эkh+1(P, th+1) Эlh(P, th) имеет решение Plh(th), а для топологии Эkh+1(P, th+1)

{Эlh(P, th) Эjh(P, th)} – решение P′′lh(th) и эти решения не совпадают. Тогда компромиссное (согласованное) решение

P'lh(th) = Arg extr Fl'

Fl' = Fl'{Plh(th), P′′lh(th), P'lh(th)}, (Пн.15)

где Fl' – целевая функция компромисса.

Случаи (Пн.13)–(Пн.15) исчерпывают возможные варианты изменения масштабов на границах уровней систем управления производством и определяют простейшую (минимальную) базовую трехуровневую структуру, учитывающую эти изменения. Такая топология (структура) широко используются в дальнейшем изложении в силу следующих причин:

1) из-за разнообразия структур системы управления производством целесообразно выделить базовую (типовую) структуру;