
УМФ Билеты
.doc-
Неоднородные задачи математической физики. Метод сведения к однородной задаче. Пример.

Пример.


-
Метод Гринберга.




-
Задача Дирихле для прямоугольника. Метод сведения к однородной задаче.

-
Задача Дирихле для прямоугольника. Метод Гринберга.



-
Задача о вынужденных колебаниях круглой мембраны. Метод Гринберга.




-
О сходимости рядов, получающихся при решении методом Гринберга. Способы улучшения сходимости.



-
Задача о распределении температуры в пластине.


-
Задача о нагревании бесконечного цилиндра.


-
Задачи математической физики с разделяющимися переменными с непрерывным спектром. Классификация задач Штурма – Лиувилля. Интегральное разложение, связанное с задачей Штурма – Лиувилля:
 ограничено.
ограничено.



-
Интегральные разложения, связанные с задачей Штурма – Лиувилля:
 граничные условия I,
II
и III
рода.
граничные условия I,
II
и III
рода.




-
Интегральное разложение, связанное с задачей Штурма – Лиувилля:
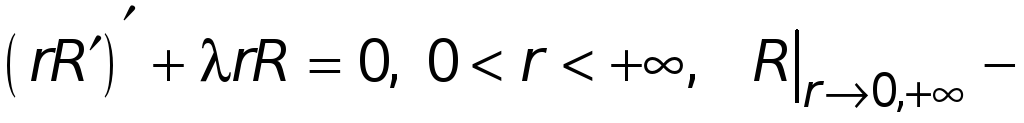 ограничено.
ограничено.

-
Задача об охлаждении полубесконечного тела.



-
Задача Дирихле для полуплоскости.




-
Задача Дирихле для полупространства.



-
Задача о радиальных колебаниях газа.




-
Интегральные преобразования.





-
Решение задачи Дирихле для полуполосы.



-
Задача об изгибе плиты.



-
Преобразование Лапласа. Определение. Таблица преобразования Лапласа.





-
Свойства преобразования Лапласа.






-
Обращение преобразования Лапласа. Интеграл Римана – Меллина. Методы обращения. Примеры.



![]()







-
Применение преобразования Лапласа к интегрированию обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами. Пример.




-
Применение преобразования Лапласа к интегрированию систем обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами. Пример.


-
Применение преобразования Лапласа к интегрированию обыкновенных линейных дифференциальных уравнений с переменными коэффициентами. Пример.




-
Применение преобразования Лапласа к интегрированию дифференциальных уравнений в частных производных.



-
Метод преобразования Лапласа. Задача о колебаниях полубесконечного стержня.


-
Метод преобразования Лапласа. Задача о продольных колебаниях конечного стержня.



-
Метод преобразования Лапласа. Задача о движении заряженной частицы в магнитном поле.



