Ответы по Matemat_logike2013
.doc
 ФЕДЕРАЛЬНОЕ
АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ
АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
Федеральное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет водных коммуникаций»
Кафедра Комплексного обеспечения информационной безопасности
Дисциплина "Математическая логика и теория алгоритмов" ( ИЗ - I )
Специальность "090900.62 - Информационная безопасность" профиль "Безопасность автоматизированных систем"
Список вопросов
-
Свойства операций над множествами.
Свойства операций над множествами.
Из определений объединения и пересечения множеств следует, что операции пересечения и объединения обладают следующими свойствами :
-
Коммутативность.
A B=B A(объединение) A B=B A(Пересечение)
-
Ассоциативность.
(A B) C=A (B C) (A B) C= A (B C)
-
Дистрибутивность.
(A B) C = (A C) (B C) (A B) C= (A C) (B C)
-
A A=A, A A=A A = A, A
-
Законы де Моргана (законы двойственности).
1) A B= A B 2 ) A B= A B
Доказательство данных свойств проводится на основе определения равенства двух множеств.
Заметим, что закон ассоциативности при комбинировании операций объединения и вычитания, вообще говоря, не имеет места.
-
Отношения: инъекция, сюръекция, биекция, их свойства.
Определение 9 ( инъекция , сюръекция , биекция ).
Отображение называется инъекцией , если для любых элементов x1, x2 X , для которых f(x1) = f(x2) следует, что x1 = x2 . (рис. 7)
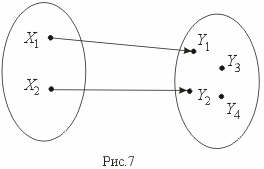
Сюръекцией (или отображением "на" ) называется отображение, при котором f(X) = Y (рис. 8).
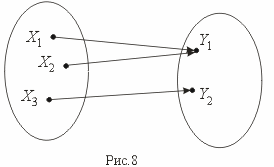
Биекция – это одновременно и сюръекция и инъекция (рис.9).
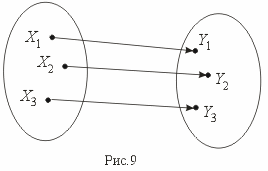
-
Отношение эквивалентности. Классы эквивалентности, их свойства.
Важным видом бинарного отношения является отношение эквивалентности.
Определение 5.1. Бинарное отношение на множестве X называется отношением эквивалентности на X, если рефлексивно, симметрично и транзитивно.
Отношение
эквивалентности часто обозначают
символами ~,![]() .
.
Примерами отношения эквивалентности служат:
-
отношение тождества IX = {(a, a)|a
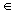 X}
на непустом множестве X;
X}
на непустом множестве X; -
отношение подобия на множестве фигур плоскости;
-
отношение равносильности на множестве уравнений;
Классы эквивалентности(свойства классов эквиваленции Посмотреть в В лекциях http://cs323524.vk.me/v323524284/784a/W4Q9tq-p7aY.jpg )
С отношением эквивалентности тесно связано разбиение множества на классы.
Определение 6.1. Система непустых подмножеств
{M1, M2, …}
множества M называется разбиением этого множества, если
M =
M1![]() M2
M2![]() …
…
и
при i![]() j
j
Mi![]() Mj =O.
Mj =O.
Сами множества M1, M2, … называются при этом классами данного разбиения.
Примерами разбиений служат:
-
разложение всех многоугольников на группы по числу вершин - треугольники, четырехугольники, пятиугольники и т. д.;
-
разбиение всех треугольников на классы подобных треугольников;
-
разбиение множества всех учащихся данной школы по классам.
Классом эквивалентности, порождённым элементом х называется подмножество множества χ.
Теорема 6.1.
Всякое разбиение ![]() непустого
множества M на
классы определяет (индуцирует) на этом
множестве отношение эквивалентности
такое, что:
непустого
множества M на
классы определяет (индуцирует) на этом
множестве отношение эквивалентности
такое, что:
-
всякие два элемента одного класса находятся в отношении ;
-
всякие два элемента различных классов не находятся в отношении .
-
Отношения частичного и линейного порядка. Теорема об изоморфизме частично упорядоч. множеств.


Непустое множество X с заданным на этом множестве отношением частичного (линейного) порядка называется частично (линейно) упорядоченным множеством. Для отношения порядка на произвольном множестве часто используют символ <=, соответственно для строгого порядка можно использовать символ ≺
Два частично упорядоченных множества называются изоморф-
ными, если между ними существует изоморфизм, то есть взаимно
однозначное соответствие, сохраняющее порядок. (Естественно, что
в этом случае они равномощны как множества.) Можно сказать так:
биекция f : A → B называется изоморфизмом частично упорядочен-
ных множеств A и B, если
a1 6 a2 ⇔ f(a1) 6 f(a2)
для любых элементов a1, a2 ∈ A (слева знак 6 обозначает порядок в
множестве A, справа — в множестве B).
Очевидно, что отношение изоморфности рефлексивно (каждое
множество изоморфно самому себе), симметрично (если X изоморф-
но Y , то и наоборот) и транзитивно (два множества, изоморфные
третьему, изоморфны между собой). Таким образом, все частично
упорядоченные множества разбиваются на классы изоморфных, ко-
торые называют порядковыми типами.
-
Равносильность формул. Основные свойства.

-
Основные тавтологии.

-
Правильные рассуждения. Основные схемы.
Правильным называется рассуждение, в котором из конъюнкции посылок следует заключение, и оно является тавтологией. В этом случае, если посылки – истинны, заключение – истинно.
В этом случае, если посылки – истинны, заключение – истинно.
А⇒В ≡ (А⇒В) ∨ Л ≡ ¬(А⇒В) ⇒(С & ¬С) ≡ (А & ¬В) ⇒(С & ¬С).
А⇒В ≡¬А ∨ В ≡ (¬А ∨ В) ∨ (С & ¬С) ≡¬ (¬А ∨ В) ⇒ (С & ¬С)
А⇒В ≡¬А ∨ В ≡ (¬А ∨ В) ∨¬А ≡¬ (¬А ∨ В) ⇒¬А ≡(А & ¬В) ⇒¬А
А⇒В ≡¬А ∨ В ≡ (¬А ∨ В) ∨ В ≡¬ (¬А ∨ В) ⇒ В≡ (А & ¬В) ⇒В
А⇒В≡ ¬А ∨ В ≡ В ∨ ¬А ≡ ¬В ⇒¬А – закон контрапозиции
-
Двойственные формулы. Лемма. Теорема – принцип двойственности.
НЕПОЛНЫЙ ОТВЕТ!!!!!!!!
Связки & и ∨ Называются двойственными.
Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций.( & на ∨)(∨ на &). Для таких формул есть свойство:
F*(X1…Xn)= -F(-X1…-Xn)
-
Теорема о представлении булевой функции формулой логики высказываний.
Каждая булева функция порождается некой формулой, в которую кроме пропозиц.переменных входят только пропозиц.связки из множества(И, ИЛИ, НЕ)
Док-во.
Пусть F(X1-Xn) задана таблицей
1)Если она является тождественным нулём, то формула (А1 & ¬А1)∨ (А2 & ¬А2)∨...∨ (Аn & ¬Аn) является такой порождающей формулой.
2) Пусть среди значений функции есть хотя бы одна 1. Пусть это строка таблицы истинности с номером j.
Эта формула принимает значение Истина только на «своей» строистинности. На всех остальных она принимает значение Ложь
f=D1vD2v…vDn составленная по всем строкам со значением 1 является формулой порождающей исходную булеву функцию
-
Полные системы связок.

-
Дизъюнктивная нормальная форма. Совершенная ДНФ. Теорема о представлении в ДНФ.



-
Теоремы о приведении к СДНФ и об единственности СДНФ.

-
Конъюнктивная нормальная форма. Совершенная КНФ. Теорема о представлении в КНФ.


-
Теорема о представимости булевых функций многочленами Жегалкина.


-
Приложение логики высказываний: к синтезу логических схем вычисл. устройств, и др.
http://cs323524.vk.me/v323524284/7907/ilnj3Kv_tSs.jpg
http://cs309131.vk.me/v309131284/6914/enoGWqwlJ90.jpg
-
Простейшие свойства выводимых формул в аксиоматических теориях (1- 8).

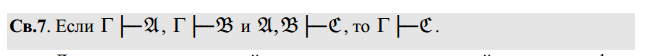

-
Вывод в теории Черча:
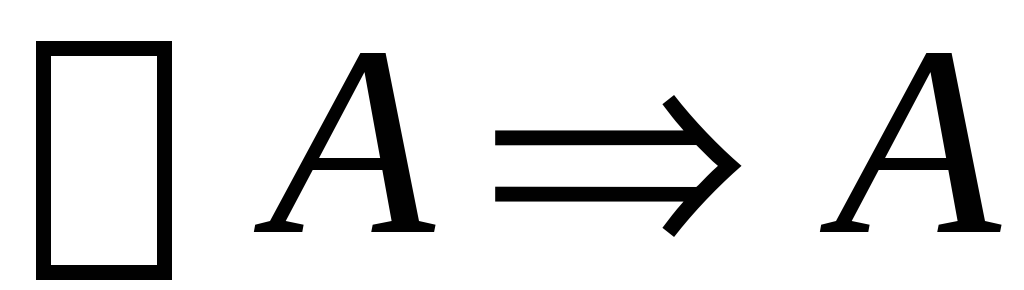 .
.


-
Вывод в теории Черча: если
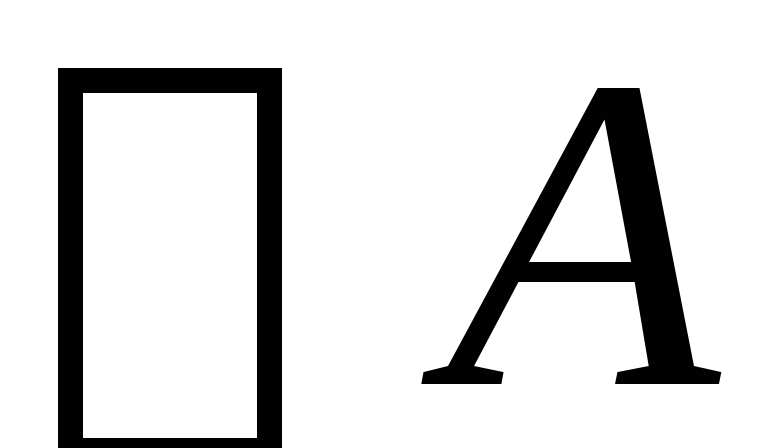 ,
то
,
то
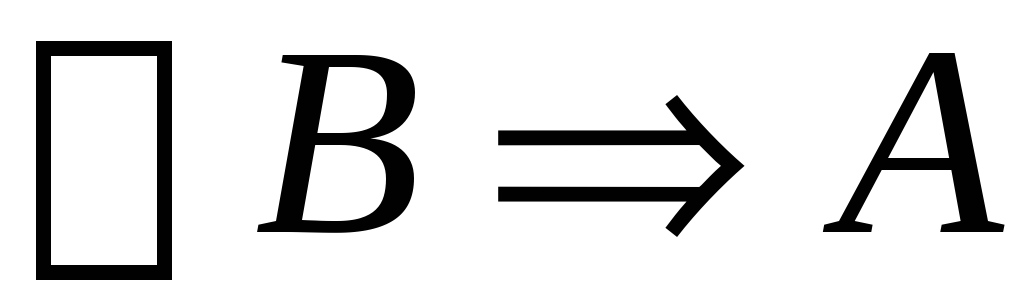 .
.

-
Вывод в теории Черча:
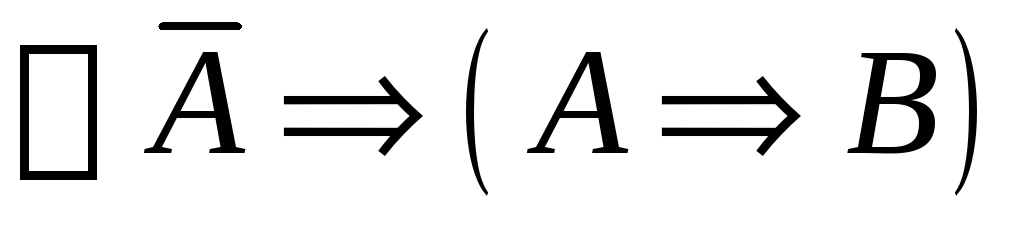 .
.

-
Вывод в теории Черча:
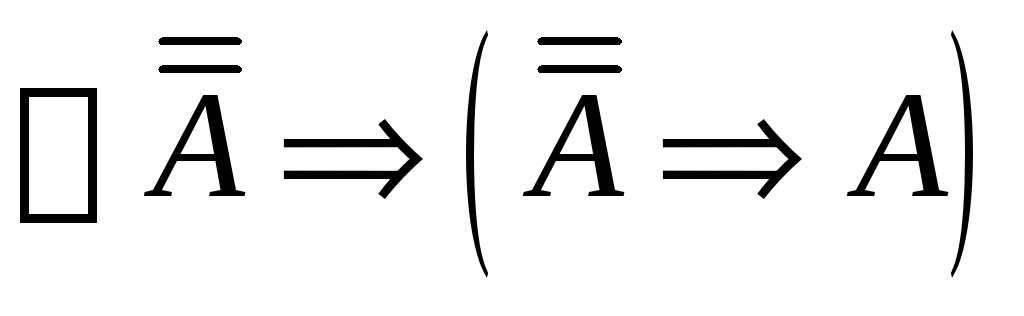 .
.

-
Вывод в теории Черча:
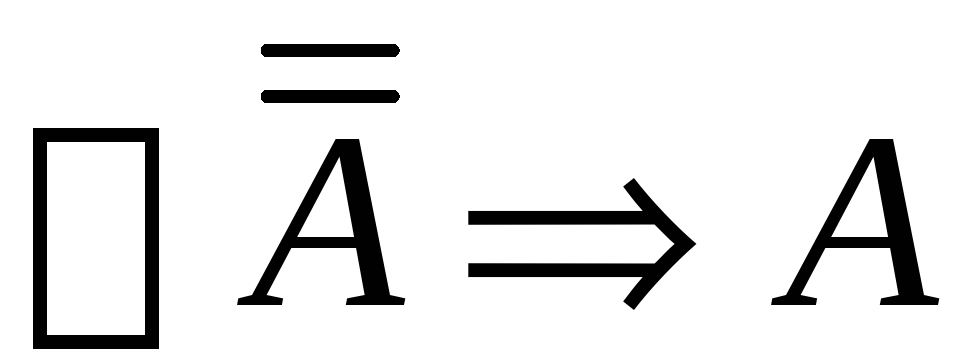 и
и
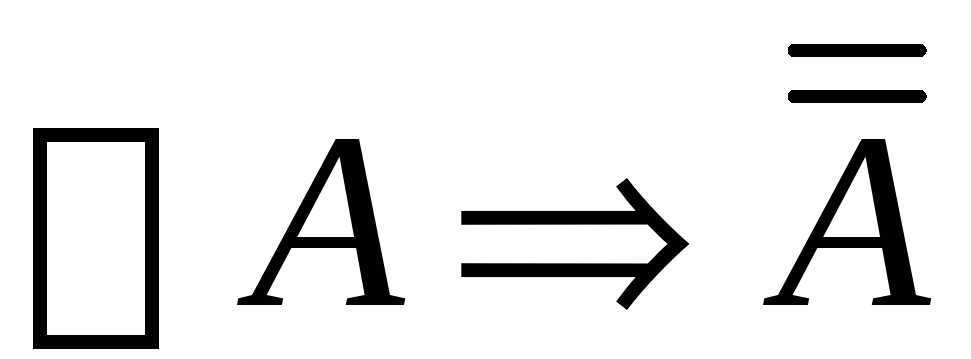 .
.

-
Теорема о дедукции.

![]()


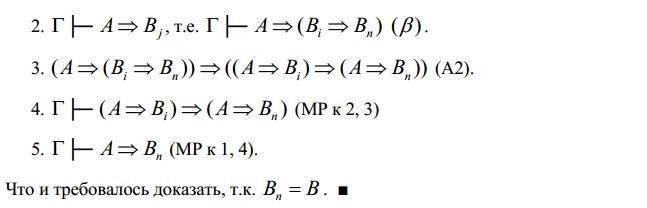
-
Правило силлогизма.

-
Вывод формулы:
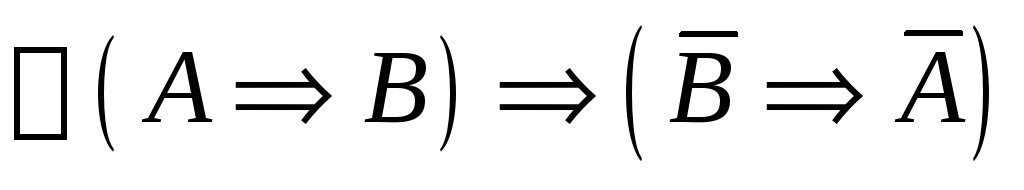 .
.

-
Правило перевертывания.


-
Производное правило вывода:
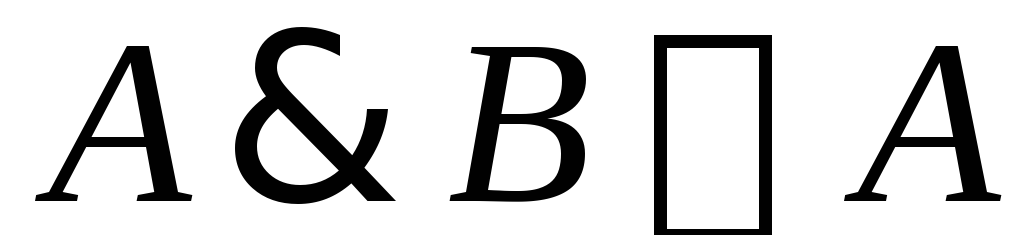 .
.

-
Производное правило вывода:
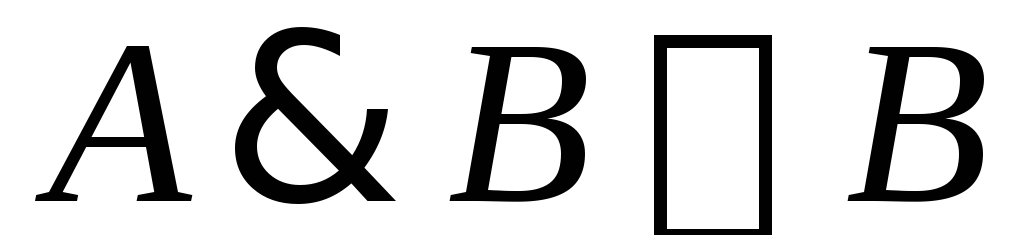 .
.

-
Производное правило вывода:
 .
.

-
Производное правило вывода:
 и
и
 .
.

-
Производное правило вывода: если
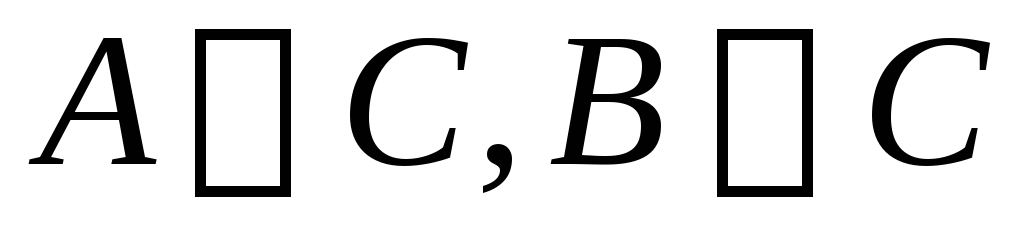 ,
то
,
то
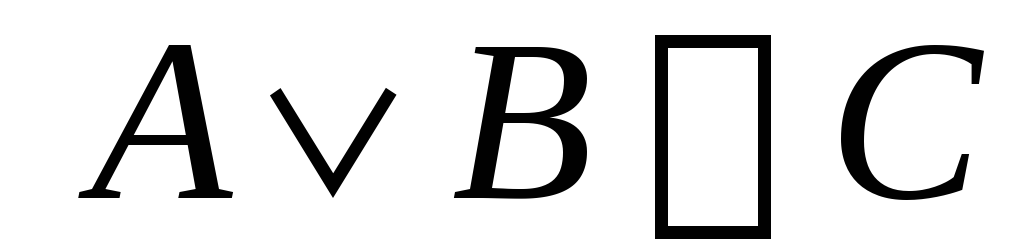

-
Производное правило вывода: если
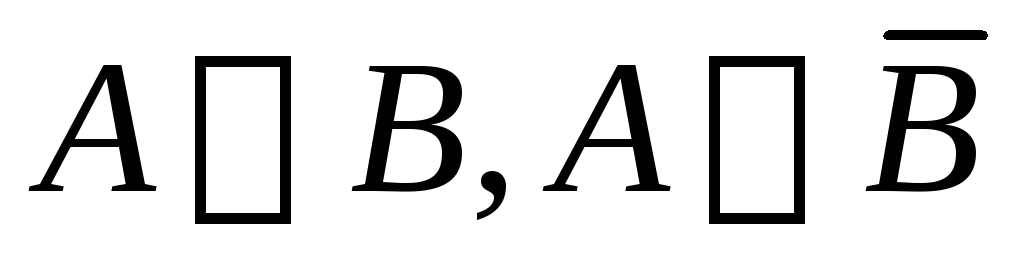 ,
то
,
то
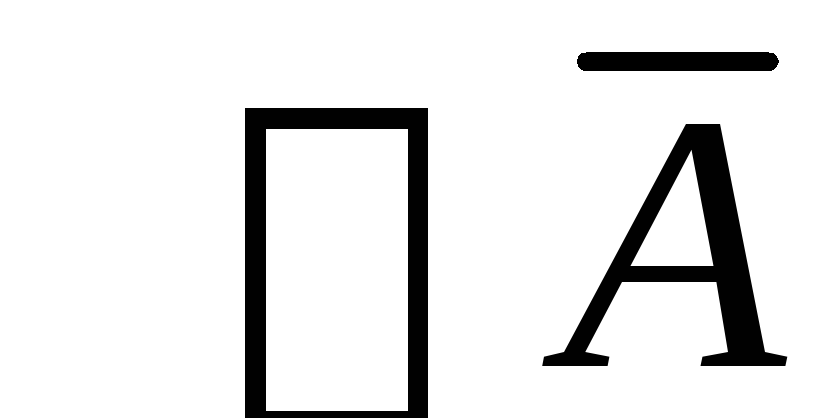 .
.

-
Лемма к теореме о полноте (в широком смысле).

-
Теорема о корректности АТЧ.
Теорема. (о корректности АТЧ)
Любая теорема АТЧ является тавтологией.
Доказательство
Аксиомы А1, А2, А3 являются тавтологиями (см. стр. 8). Далее, единст-39
венное правило вывода MP, примененное к тавтологиям, снова приводит к
тавтологии (см. стр. 9). Поэтому каждая теорема является тавтологией. ■
-
Теорема о полноте (в широком смысле).

-
Теорема о непротиворечивости.

-
Теорема о абсолютной непротиворечивости. Теорема об альтернативности АТ.

-
Частично–рекурсивные и примитивно–рекурсивные функции:
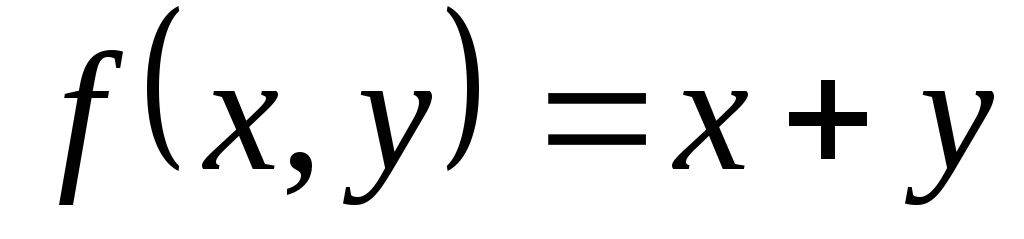 ;
;
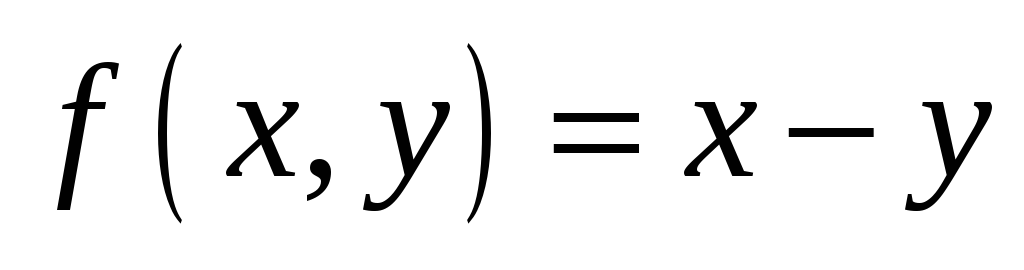 .
. -
Машина Тьюринга для простейших функций.
-
Машина Тьюринга для копирования слов.

-
Машина Тьюринга для удвоения чисел.
-
Машина Тьюринга для сложения двух чисел