5.3 Устойчивость
Дискретная схема называется устойчивой, если при каждом шаге по маршевой28 координате случайная ошибка решения не возрастает при переходе от одного шага к другому.
В
качестве примера, рассмотрим решение
нестационарного уравнения теплопроводности
(21) при помощи явной разностной схемы
(22а). Соотношение шагов расчетной сетки
Δt
и Δх выберем таким, чтобы выполнялось
условие
.
Пусть в начальный момент времени
температура центрального узла составляет
один градус, а температура остальных
узлов – нулевая. Граничные условия
также примем нулевыми.
Результаты расчета для первых четырех шагов по времени на расчетной сетке, состоящей из девяти узлов, приведены в табл. 5.1. Как следует из этой таблицы, полученные результаты полностью противоречат физическому смыслу – вместо постепенного выравнивания температуры по длине стержня, наблюдается её скачкообразное изменение во всех узлах расчетной сетки, причем амплитуда колебаний постоянно нарастает – решение "идет в разнос".
Таблица 5.1
|
Номер узла сетки |
Номер шага по времени | ||||
|
0 |
1 |
2 |
3 |
4 | |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
-4 |
|
2 |
0 |
0 |
1 |
-3 |
10 |
|
3 |
0 |
1 |
-2 |
6 |
-16 |
|
4 |
1 |
-1 |
3 |
-7 |
19 |
|
5 |
0 |
1 |
-2 |
6 |
-16 |
|
6 |
0 |
0 |
1 |
-3 |
10 |
|
7 |
0 |
0 |
0 |
1 |
-4 |
|
8 |
0 |
0 |
0 |
0 |
0 |
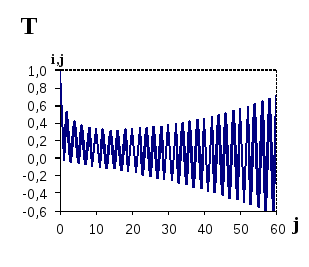
На рис. 14а приведен график, демонстрирующий изменение температуры в центральном узле расчетной сетки для случая r=0,513. В этом случае также наблюдаются осцилляции с нарастающей амплитудой, однако, даже после шестидесяти шагов по времени, амплитуда колебаний не превышает одного градуса. Можно доказать, что уменьшение параметра r (за счет уменьшения шага по времени Δt по отношению к шагу Δх) до величины 0,5 полностью ликвидирует осцилляции и позволяет получить физически обоснованное решение. В качестве примера, на рис. 14б приведена зависимость температуры от номера шага по времени для случая r=0,30.
Потеря устойчивости при чрезмерном увеличении шага по маршевой координате характерна для всех явных расчетных схем. Следует отметить, что упомянутое условие устойчивости разностной схемы (22а) r≤0,5 является весьма "жестким". Дело в том, что попытка уменьшения шага по пространственной координате в два раза, вынудит исследователя одновременно уменьшить шаг по времени в четыре раза. В одномерном случае это приведет к увеличению трудоемкости расчета в восемь раз, в двумерном – в шестнадцать раз, а в трехмерном случае трудоемкость расчета возрастет в тридцать два раза!
Простейший практический способ оценки устойчивости разностной схемы заключается в умышленном внесении некоторого возмущения в исходные данные задачи и последующем изучении распространения этого возмущения, подобно тому, как это было сделано в вышеприведенном примере.
К настоящему времени разработан ряд теоретических методов исследования устойчивости линейных дифференциальных уравнений в частных производных, но их изложение выходит за рамки данной работы.
|
а) r=0,513 |
б) r=0,30 |
|
Рис. 14. Зависимость температуры в центральном узле сетки (i=4) от номера шага по времени | |