
- •1.Основные понятия теории алгоритмов.
- •2.Примитивно рекурсивные функции. Базис элементарных функций. Операции подстановки и примитивной рекурсии.
- •3.Примитивно рекурсивные функции. Основные свойства операций подстановки и примитивной рекурсии.
- •4.Примитивно рекурсивные функции относительно совокупности функций. Основные свойства.
- •5.Производные операции над функциями.
- •6.Операции конечного суммирования и конечного произведения.
- •7.Предикат, логическая функция. Логические операции с предикатами.
- •8.Операции навешивания кванторов. Операции навешивания кванторов относительно двуместных предикатов
- •9.Примитивно рекурсивный предикат.
- •10. Операция навешивания ограниченного квантора над предикатами
- •11. Кусочное задание функции.
- •12 Операция ограниченной минимизации.
- •13.Частично рекурсивные функции.
- •14. Машина Тьюринга (мт). Применение мт к словам
- •16. Вычислимые по Тьюрингу функции.
- •17. Правильная вычислимость функций на машине Тьюринга.
- •18. Вычислимость по Тьюрингу примитивно рекурсивных функций. Суперпозиция.
- •19. Вычислимость по Тьюрингу примитивно рекурсивных функций. Примитивная рекурсия.
- •20. Вычислимость по Тьюрингу частично рекурсивных функций.
- •22. Нормальные алгоритмы Маркова и их применение к словам.
- •23. Нормально вычислимые функции и принцип нормализации Маркова.
- •15.Конструирование мт. Операции над машинами Тьюринга.
8.Операции навешивания кванторов. Операции навешивания кванторов относительно двуместных предикатов
Пусть на множестве М задан одноместный предикат p(x).
Определение.
Будем
говорить, что выражение вида
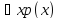 на множествеM
представляет собой истинное высказывание,
тогда и только тогда, когда p(x)
истинно для любого элемента xϵ
M.
на множествеM
представляет собой истинное высказывание,
тогда и только тогда, когда p(x)
истинно для любого элемента xϵ
M.
Из определения
следует, что если p(x)
истинно на множестве M,
то высказывание
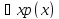 тоже истинно на этом множестве;
тоже истинно на этом множестве;
и в случае, когда
p(x)
ложно на множестве M,
то высказывание
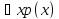 - тоже является ложным на данном
множестве;
- тоже является ложным на данном
множестве;
Определение.
Будем говорить, что выражение
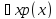 на множествеM
представляет собой истинное высказывание,
тогда и только тогда, когда p(x)
- истинно хотя бы для одного элемента
из этого множества.
на множествеM
представляет собой истинное высказывание,
тогда и только тогда, когда p(x)
- истинно хотя бы для одного элемента
из этого множества.
Определение.
Выражение
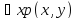 при
при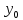 ϵ
M
представляет собой высказывание
ϵ
M
представляет собой высказывание
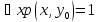 (истинное высказывание) тогда и только
тогда, когда
(истинное высказывание) тогда и только
тогда, когда – истинно для любого элементаxϵ
M.
– истинно для любого элементаxϵ
M.
Определение.
Выражение
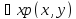 при
при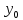 ϵ
M
представляет собой высказывание
ϵ
M
представляет собой высказывание
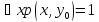 (истинное высказывание) тогда и только
тогда, когда
(истинное высказывание) тогда и только
тогда, когда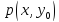 – истинно для любого элементаx
ϵ
M.
– истинно для любого элементаx
ϵ
M.
Определение.
Выражение
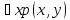 при заданном
при заданном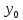 ϵ
M
представляет высказывание
ϵ
M
представляет высказывание
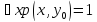 (истинное высказывание), тогда и только
тогда, когда
(истинное высказывание), тогда и только
тогда, когда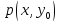 -
истинно хотя бы для одного элемента из
множестваM.
-
истинно хотя бы для одного элемента из
множестваM.
Таким образом, операции навешивания кванторов (всеобщности и существования) к двуместным предикатам приводит к одноместному предикату, т.е.
 (13)
(13)
 (14)
(14)
Если множество М,
на котором рассматривается предикат
р(х)
является конечным множеством, т.е. M={ ,
то высказывание вида
,
то высказывание вида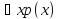 тождественно
равно высказыванию
тождественно
равно высказыванию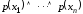 ,
т.е. имеет место следующее равенство
,
т.е. имеет место следующее равенство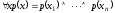 .
(15)
.
(15)
Аналогично, если
множество М, на котором рассматривается
предикат р(х)
является конечным множеством, т.е. M={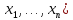 ,
то высказывание вида
,
то высказывание вида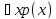 тождественно равно высказыванию
тождественно равно высказыванию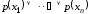 ,
т.е. имеет место следующее равенство
,
т.е. имеет место следующее равенство
 .
(16)
.
(16)
9.Примитивно рекурсивный предикат.
Определение.
Функция
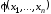 называется представляющей функцией
для предиката
называется представляющей функцией
для предиката ,
если выполняются следующие условия:
,
если выполняются следующие условия:
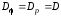 ,
т.е. их область определения совпадают;
,
т.е. их область определения совпадают;для любого набора
 из области определенияD
из области определенияD
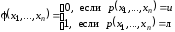 (17)
(17)
Определение. Предикат р(х) называется примитивно рекурсивным, если его представляющая функция является примитивно рекурсивной функцией.
Определение.
Функция
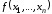 называется ПРФ относительно совокупности
функций и предикатов
называется ПРФ относительно совокупности
функций и предикатов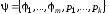 ,
если она ПРФ относительно совокупности
функций
,
если она ПРФ относительно совокупности
функций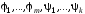 ,
где
,
где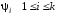 - представляющая функция предиката
- представляющая функция предиката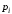 .
.
Определение.
Предикат
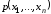 называется ПРФ относительно совокупности
функций и предикатов
называется ПРФ относительно совокупности
функций и предикатов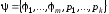 ,
если представляющая функция предикатаp
является примитивно рекурсивной
относительно совокупности функций
,
если представляющая функция предикатаp
является примитивно рекурсивной
относительно совокупности функций
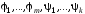 ,
где
,
где - представляющая функция предиката
- представляющая функция предиката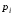 .
.
Теорема 2. Логические операции над предикатами сохраняют свойства примитивной рекурсивности предикатов.
10. Операция навешивания ограниченного квантора над предикатами
Пусть
задан двуместный предикат p(x,y),
где в общем случае
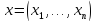 .
.
Определение.
Говорят, что предикат R(x,z)
получен из предикат p(x,y)
с применением операции навешивания
ограниченного квантора существования,
т.е.
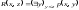 ,
если выполняется следующее равенство:
,
если выполняется следующее равенство:
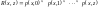 .
(27)
.
(27)
Определение.
Говорят, что предикат Q(x,z)
получен из предиката p(x,y)
с применением операции навешивания
ограниченного квантора всеобщности,
т.е.
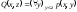 ,
если выполняется следующее равенство:
,
если выполняется следующее равенство:
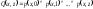 .
(28)
.
(28)
Приведем пример. Пусть
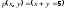 .
.
Рассмотрим
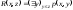
и
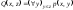 .
.
Очевидно
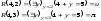
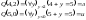
Теорема 3. Операция навешивания ограниченных кванторов существования и всеобщности сохраняет свойство примитивной рекурсивности функций относительно совокупности{p}.
Доказательство.
Пусть задан
предикат p(x,y)
и
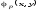 –представляющая
его функция и пусть
–представляющая
его функция и пусть
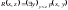 .
.
Представляющую
функцию предиката R(x,
z)
обозначим через
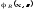 и покажем, что ее можно представить
следующим образом
и покажем, что ее можно представить
следующим образом
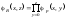 .
(29)
.
(29)
Действительно:
пусть предикат
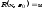 .
.
Тогда по определению операции навешивания ограниченного квантора существования,
найдется
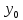 такое, что
такое, что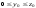 и
и ,
следовательно
,
следовательно
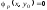 .
Отсюда следует, что
.
Отсюда следует, что
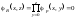 .
.
Предположим, что предикат
 .
.
Тогда
по определению операции навешивания
ограниченного квантора существования,
для любого набора (x,y),
p(x,y)=л,
следовательно
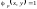 и
и
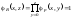 .
.
Т.
к. ранее у нас было доказано, что операция
конечного произведения обладает
свойством примитивной рекурсивности,
то
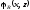 является примитивно рекурсивной
относительно совокупности
является примитивно рекурсивной
относительно совокупности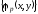 .
.
Пусть
 .
.
Аналогично доказывается случай, когда задана операция навешивания ограниченного квантора всеобщности. Легко можно доказать, что в качестве представляющей функции предиката Q(x,z) можно брать
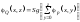 (30)
(30)
и
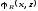 является ПРФ относительно совокупности
является ПРФ относительно совокупности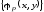 .
В виде упражнение докажите самостоятельно.
.
В виде упражнение докажите самостоятельно.
Пусть
задана совокупность функций
 и совокупность предикатов
и совокупность предикатов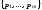 .
.
Определение.
Ф-я f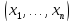 ,
наз-cя
ПРФ относит-о заданной совокупности
функций и предикатов, если она ПРФ
относительно совок-ти
,
наз-cя
ПРФ относит-о заданной совокупности
функций и предикатов, если она ПРФ
относительно совок-ти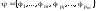 ,
где
,
где представляющая функция предиката
представляющая функция предиката ,
,
