5. Доказательство закона (теоремы)
Харди-Вайнберга
Следует доказать два утверждения закона Харди-Вайнберга:
1. Доказать, что частоты аллелей в родительской и дочерней популяции одинаковы.
2. Доказать, что частоты генотипов в родительской и дочерней популяции также одинаковы.
В популяциях автотетраплоидов (сорта ржи, гречихи, кормовых трав) значительная часть генотипов является гетерозиготами (симплексы, дуплексы, триплексы).
При p=q=0,5 доля гомозигот (нулиплексы, квадриплексы) составляет незначительную часть популяции. У диплоидов же при p=q=0,5 половина особей популяции – гомозиготы.
Равновесие у полиплоидов не может быть достигнуто за одно поколение размножения, поскольку у полиплоидов возрастает число генотипов гамет и для достижения равновесия требуется нескольких поколений размножения.
Равновесные доли пяти генотипов в популяции автотетраплоидов задаются выражением:
7. Закон стабилизирующего скрещивания к. Пирсона (1904 г):
1. Если популяция не находится в состоянии равновесия, то равновесие при случайном скрещивании достигается через одно поколение и не зависит от первоначального состава популяции.
2. Все популяции с одними и теми же частотами генов (хотя частоты генотипов могут и различаться) при случайном подборе пар придут к одному и тому же равновесному состоянию.
11. Для установления соответствия между фактическими частотами генотипов и теоретически ожидаемыми по закону Харди-Вайнберга проводят вычисления в следующем порядке:
Определяют частоту аллелей по формуле Р.Фишера.
2. Рассчитывают теоретические частоты генотипов по формуле Харди-Вайнберга.
3. Определяют теоретические численности генотипов.
4. Рассчитывают критерий (хи-квадрат).
5. Находят табличное значение критерия хи-квадрат.
Если расчетная величина хи-квадрат меньше табличной, то частоты генотипов в изучаемой популяции соответствуют равновесию Харди-Вайнберга.
Критерий соответствия (хи-квадрат) рассчитывают по следующей формуле:
где О и Е – наблюдаемые и теоретически ожидаемые количества генотипов определённого типа, а k – число генотипических (фенотипических) классов.
Табличное значение хи-квадрат находят по числу степеней свободы и уровню значимости в специальной таблице.
Степень свободы определяет значимость величины хи-квадрат и равна числу фенотипических (генотипических) классов k минус единица и минус число оцениваемых параметров (число независимых величин).
При кодоминировании число фенотипических классов, число оцениваемых параметров и число степеней свободы определяют по формулам
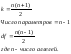
Уровень значимости обычно принимается равным 0,05 д.е. или 5%. Это означает, что гипотезу решено считать не соответствующей наблюдениям, если вероятность того, что расхождение между теоретически ожидавшимися и наблюдаемыми в эксперименте данными, обусловленное только случайными причинами, составляет не более 5%.
Пример
У людей имеются два аллеля в локусе . В выборке из 200 человек обладатели различных генотипов распределились следующим образом:
-108
-86
-6
Всего 200
Следует установить, соответствуют ли эти данные частотам, которых следует ожидать, исходя из равновесия Харди-Вайнберга.
Частоты аллелей:
Теоретические частоты генотипов:
Теоретические численности генотипов:
Хи-квадрат фактический:
Число степеней свободы:
При
числе степеней свободы df=1
и уровне значимости P=0,05
(5%) хи-квадрат табличный (
) равен 3,84.
Вывод:
Поскольку фактический критерий хи-квадрат больше табличного (5,26 >3,84), то величина 5,26, статистически достоверна при 5%-ном уровне значимости. Следовательно следует отвергнуть гипотезу о соответствии частот указанных трёх генотипов равновесию Харди-Вайнберга.