Введение в математику

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

"Алтайский государственный технический университет им. И. И. Ползунова"

И. Э. Головичева, В. В. Лодейщикова

ВВЕДЕНИЕ В МАТЕМАТИКУ

Учебно-методические указания

Барнаул 2013

ÓÄÊ 517 (075.5)

Головичева, И. Э. Введение в математику: учебно-методические указания/ И. Э. Головичева, В. В. Лодейщикова. Барнаул: Изд-во АлтГТУ, 2013. 77 с.

Учебно-методические указания содержат материал для изучения в 1 семестре дисциплины "Введение в математику" для всех направлений бакалавриата технического ВУЗа. Указания включают в себя три главы: элементы теории множеств, комплексные числа и многочлены, функции одной действительной переменной. Каждая глава содержит необходимый теоретический материал, сопровождаемый большим количеством примеров и задач с подробными решениями, а также задачи для самостоятельного решения с ответами.

Рассмотрены и одобрены на заседании кафедры "Высшая математика"АлтГТУ. Протокол 1 от 29.08.2013 г.

Рецензент: Вингисаар Э. И. к.ф.-м.н., доцент

2

Оглавление

1.1Основные понятия. Операции над множествами . . . . . . . . . . 9

1.2Числовые множества . . . . . . . . . . . . . . . . . . . . . . . . . . 12

2.1Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

2.2Формы записи комплексных чисел . . . . . . . . . . . . . . . . . . 17

2.3 Возведение в степень и извлечение корней из комплексных чисел 20

2.4Многочлены. Делимость многочленов . . . . . . . . . . . . . . . . 25

2.5Корни многочлена. Разложение на множители. . . . . . . . . . . . 28

3.3Операции над функциями . . . . . . . . . . . . . . . . . . . . . . . 44

3.4Основные элементарные функции и их графики. Элементарные функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

3.5Дробно-рациональные функции . . . . . . . . . . . . . . . . . . . . 51

3.6Преобразования графиков функций. Построение плоских областей 59

3

4

Предисловие

Данные учебно-методические указания предназначены, в первую очередь, для студентов первого курса, изучающих дисциплину "Введение в математику". Каждая глава содержит основные теоретические сведения и формулы, необходимые для решения задач. Изложение теоретического материала по всем темам сопровождается рассмотрением большого количества примеров.

Для сокращения записей иногда будем использовать некоторые простейшие логические символы:

=) означает "из предложения следует предложение ";

() "предложения и равносильны", т. е. из следует и из

следует ; 8 означает "для любого", "для всякого";

9 "существует","найдется"; : "такое, что".

Так как данный курс опирается на знания, полученные в школе, то сделаем обзор оcновных формул элементарной математики.

Обзор основных формул элементарной математики

Формулы сокращенного умножения

(a + b)2 = a2 + 2ab + b2,

(a b)2 = a2 2ab + b2, a2 b2 = (a b)(a + b),

a3 b3 = (a b)(a2 + ab + b2), a3 + b3 = (a + b)(a2 ab + b2),

(a + b)3 = a3 + 3a2b + 3ab2 + b3,

(a b)3 = a3 3a2b + 3ab2 b3.

5

Степени и корни

Пусть n натуральное число, a действительное число, тогда

an = a a : : : a,

(корень четной степени из отрицательного числа не определен)

Далее, пусть a > 0, b > 0, m; n действительные числа, тогда

Квадратное уравнение

ax2 + bx + c = 0, a 6= 0,

D = b2 4ac,

p

x1;2 = b D.

2a

Теорема Виета

b c

x1 + x2 = a, x1 x2 = a, ãäå x1, x2 корни квадратного уравнения.

Квадратный трехчлен ax2 + bx + c, a 6= 0,

разложение квадратного трехчлена на множители

ax2 + bx + c = a(x x1)(x x2),

ãäå x1, x2 корни квадратного уравнения ax2 + bx + c = 0.

6

Тригонометрия

Формулы двойного угла

sin 2 = 2 sin cos ,

cos 2 = cos2 sin2 = 2 cos2 1 = 1 2 sin2 ,

2 tg tg 2 = 1 tg2 .

Формулы понижения степени

Формулы преобразования суммы в произведение

7

Формулы преобразования произведения в сумму

Логарифмы

loga b = c (a > 0; b > 0; a 6= 1) тогда и только тогда, когда ac = b.

Логарифмы по основанию 10 называются десятичными логарифмами: log10 a = lg a.

Логарифмы по основанию e (e 2; 72) называются натуральными логарифмами: loge a = ln a.

Основное логарифмическое тождество: blogb a = a. loga 1 = 0, loga a = 1,

loga bm = m loga b, logam b = m1 loga b (a > 0; b > 0; a 6= 1),

8

Элементы теории множеств

1.1Основные понятия. Операции над множествами

Понятие множества является одним из основных неопределяемых понятий математики. Под множеством понимают совокупность некоторых объектов, объединенных по какому-либо признаку.

Пример 1.1. Множество студентов в группе. Пример 1.2. Множество дней недели.

Пример 1.3. Множество целых чисел.

Множества обозначаются заглавными буквами латинского алфавита: A, B, C,. . . .

Определение 1.1. Объекты, из которых состоит множество, называются

элементами множества.

Элементы множества обозначаются малыми буквами латинского алфавита: a, b, c,. . . .

Если элемент x принадлежит множеству X, то записывают x 2 X. Если элемент x не принадлежит множеству X, то записывают x 62X. Множество,

которое не содержит ни одного элемента, называется пустым и обозначается

?.

Пример 1.4. Элемент 1 принадлежит множеству цифр в числе 214 , а элемент 3 не принадлежит данному множеству.

Основные способы задания множеств

1)Множество может быть определено непосредственным перечислением всех своих элементов. В этом случае элементы множества записывают в фигурных скобках, внутри которого они перечислены. Например, множество цифр в числе 214 может быть записано как A = f2; 1; 4g.

9

B = fb j b2 3b + 2 = 0g означает, что множество B состоит из корней указанного квадратного уравнения.

Заметим, что можно задавать и бесконечное множество. Например, A = f2; 4; 6; 8; : : : g множество четных положительных чисел.

Определение 1.2. Множество A называется подмножеством множества

B, если каждый элемент множества A является элементом множества B.

Символически это обозначают так: A B. Заметим, что для любого множества X верны включения: ? X, X X.

Пример 1.5. Перечислить все подмножества множества A = f2; 1; 4g.

Решение. Получаем 8 подмножеств данного множества: ?, f2g, f1g, f4g, f2; 1g, f2; 4g, f1; 4g, f2; 1; 4g.

Определение 1.3. Говорят, что множества A и B равны èëè совпадают

(A = B), если A B и B A. Другими словами, множества, состоящие из

одних и тех же элементов, называются равными.

Далее будем считать, что все рассматриваемые множества являются подмножествами некоторого универсального множества U. Перейдем к определению

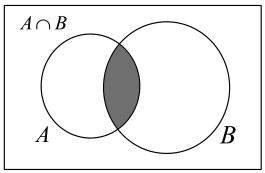
операций над множествами и будем их наглядно иллюстрировать с помощью диаграмм Эйлера-Венна. Множества будем обозначать в виде кругов, а универсальное множество U прямоугольником.

Определение 1.4. Пересечением множеств A и B называется множество

A \ B, состоящее из элементов, входящих и в A, и в B:

A \ B = fxjx 2 A è x 2 Bg:

10