
Введение в математику
.pdfВ частности, если есть n множителей и все они одинаковые, то
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zn = rn (cos(n') + i sin(n')): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Эта формула называется |
|
|
формулой Муавра. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Пример 2.4. Вычислить z6, åñëè r = 3, arg z = |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. По формуле Муавра получаем, что: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
z6 = 36 |
|
cos |
6 |
|
|
|
|
+ i sin |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
= 36 |
|
|
|
cos |
|
|
|
|
+ i sin |
|
|
|
|
|
= |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
= 3 |
(0 + i 1) = 729i: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
i! |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Пример 2.5. Вычислить |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Решение. Поскольку z = |
|
|
|
+ |
|
|
i, òî x = |
|
, y = |
|
|
|
|
|
. Модуль комплексного |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
2 |
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
= v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
i |
|
|
|
|
|
2 |
|
|
|
|
p |
|
|
|
2 = 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
r = |
1 |
|
3 |
|
1 |
|
+ |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Аргумент определим из |
системы |
уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8cos ' = 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< sin ' = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Заметим, что угол |
|
|
|
|
находится |
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
во II четверти. Значит, |
' = 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
z = 2 + |
|
23i = 1 |
|
cos |
|
23 |
|
|
+ i sin |
23 |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
По формуле Муавра получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
p |
|
|
|
17 |
= 117 cos 17 |
23 |
|
+ i sin |
17 |
23 |
|
|
= |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 + |
23i! |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
= cos |
|
3 |
|
+ i sin |
3 |
|
|
= cos 12 23 |
+ i sin 12 |
23 |
|
= |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= cos 23 |
|
+ i sin 23 |
|
|
= 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 i: |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
p |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21
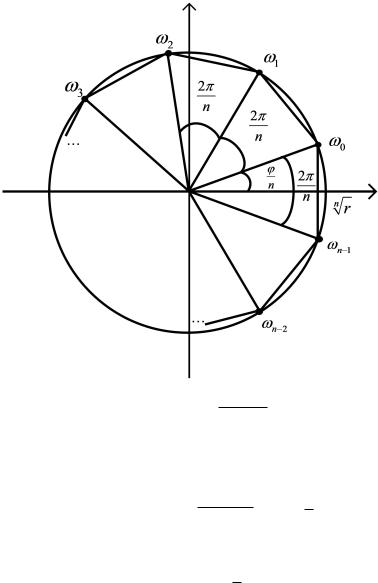
Определение 2.6. Корнем n -й степени из комплексного числа z называется комплексное число !, удовлетворяющее равенству !n = z.
Åñëè z = x + yi = r(cos ' + i sin '), òî |
|
|
|||||||
!k = pn |
|
cos |
' + 2 k |
+ i sin |
' + 2 k |
; |
|
|
|
r |
|
|
|||||||
n |
n |
|
|
||||||
ãäå k = 0; 1; : : : ; n 1. |
|
|
|
||||||
лежат на окружности радиуса |
r в вершинах |
||||||||
Все значения корня степени n |
|
|
|
pn |
|||||
правильного n -угольника.
p
Пример 2.6. Найти все значения корня 4 2 + 2i и изобразить их на комплекс- ной плоскости.
Решение. Поскольку z = 2 + 2i, то x = 2, y = 2. Модуль комплексного числа
pp
r = j2 + 2ij = 22 + 22 = 2 2:
Аргумент определим из системы уравнений:
8p
|
2 |
|
|||
>cos ' = |
|
|
|
; |
|
p2 |
|
|
|||
2 |
|
||||
> sin |
|
|
|
|
|
< |
' = |
|
|
|
: |
> |
2 |
|
|
||
> |
|
|
|
|
|
: |
|
|
|
|
|
22
Значит, |
|
' = 4 è z = 2 + 2i = 2p2 cos |
4 |
+ i sin |
4 |
|
: |
|
||||||||||||||||||||||||||||||||||||||
Получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
!k = |
4 |
|
|
|
|
|
|
0cos |
0 |
4 |
|
|
+42 k |
1 + i sin |
0 4 |
|
+42 k |
11 |
; |
|
||||||||||||||||||||||||
|
|
2p2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
ãäå |
|
|
. |
q |
|
|
|
|
|
|
@ |
@ |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
@ |
|
|
|
|
|
AA |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
k = 0; 1; 2; 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
+ i sin |
|
; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Ïðè k = 0: !0 |
= |
4 |
2p2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
p |
16 |
16 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
cos |
9 |
|
|
|
|
|
|
|
|
9 |
; |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ïðè k = 1: !1 |
= |
2p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
4 |
|
|
|
16 + i sin 16 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ïðè k = 2: !2 = 4 |
2p2 |
|
|
16 |
+ i sin |
|
16 |
|
= |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
15 |
|
|
|
|
|
15 |
; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= 4 |
|
2p2 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 + i sin 16 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ïðè k = 3: !3 = 4 |
2p2 |
|
|
cos |
16 |
|
+ i sin |
|
16 |
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
7 |
|
|
|
|
|
|
|
|
7 |
: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= 4 |
|
2p2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 + i sin 16 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
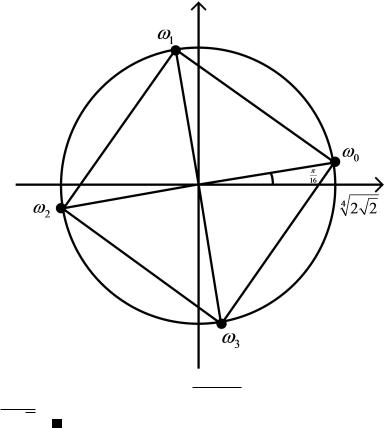
p
Получили, что все значения корня 4 2 + 2i являются вершинами квадрата с p p
диагональю 2 4 2 2.
23

Пример 2.7. Решить уравнения:
1)x2 10x + 74 = 0;
2)2x2 x + 10 = 0;
3)x2 + 16 = 0;
4)* x2 + 2x 5 3xi i = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
Для уравнения x2 10x + 74 = 0, получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
D = ( 10)2 4 1 74 = 100 296 = 196 = i2 142 = (14i)2; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x1;2 = |
10 |
(14i)2 |
= |
10 |
14i |
= 5 |
|
|
7i; x1 |
= 5 |
|
|
7i, x2 |
= 5 + 7i. |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) |
Заметим, что для уравнения 2x2 x + 10 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1 p |
D = ( 1)2 4 2 10 = 1 80 = 79 = i2 79; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
10 p |
|
|
i |
= |
|
|
|
|
|
p |
|
i; x |
|
|
|
|
|
|
|
p |
|
i, x |
|
|
|
|
|
+ |
p |
|
i. |
||||||||||||||
|
|
|
79i2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
x |
|
= |
= |
79 |
|
1 |
|
79 |
|
= |
1 |
|
79 |
|
|
= |
1 |
79 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
||||||||||||||||||||||||||
|
|
1;2 |
4 |
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
1 |
|
4 4 |
2 |
|
|
|
|
4 |
|
|
|||||||||||||||||||||||
3) |
Для уравнения x2 + 16 = 0 имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 = 16; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 = (4i)2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 = 4i, x2 = 4i. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4)* Сначала уравнение x2 + 2x 5 3xi i = 0 преобразуем к виду |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 + x(2 3i) 5 i = 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
D = (2 3i)2 4 1 ( 5 i) = 4 12i + 9i2 + 20 + 4i = 15 8i; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x1;2 = |
2 + 3i 15 8i |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
D = |
|
8i |
. Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
, ãäå |
u |
è |
|
v |
|
||||||||||||||||||||||||
|
Найдем значения |
|
|
|
15 |
|
|
|
|
|
|
|
15 8i = u + vi |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
действительные числа. Отсюда получаем, что
24

15 8i = (u + iv)2 è 15 8i = u2 v2 + 2uvi.
Приравниваем действительные и мнимые части, получаем систему уравне-
íèé: |
|
|
|
|
|
( |
2uv = |
|
|
8: |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
u2 |
v2 = 15; |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 4, v1 = 1 è u2 = 4, |
|||||||
Решая эту систему уравнений получим, что u1 |
||||||||||||||||||||||||||||
v2 = 1.p |
|
|
|
|
|
èëè p |
|
|
|
|
|
. Возьмем p |
|
|
|
|
|
. Тогда |
||||||||||
Значит, D = 4 + i |
|
|
D = 4 i |
|
|
|
|
|
|
|
|
D = 4 + i |
|
|||||||||||||||
|
|
x |
1 |
= |
2 + 3i 4 + i |
= |
4i 6 |
= |
|
3 + 2i, |
|
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
x2 |
= |
2 + 3i + 4 i |
= |
|
2 + 2i |
= 1 + i. |
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
p |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим те же результаты. |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Очевидно, что взяв D = 4 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2.4Многочлены. Делимость многочленов
Определение 2.7. Многочленом n -й степени от переменной z называется выражние вида:
f(z) = a0zn + a1zn 1 + + an 1z + an:
Здесь a0; a1; : : : ; an действительные числа, которые называются коэффициентами многочлена, a0 6= 0. Можно рассматривать и многочлены с комплексными коэффициентами.
Пример 2.8. f(z) = 3z5 + z4 z + 2 многочлен пятой степени с действительными коэффициентами.
Пример 2.9. f(z) = z2 2iz + 5 4i многочлен второй степени с комплексными коэффициентами.
Пример 2.10. Любая константа (число) является многочленом степени 0.
Определение 2.8. Многочлены f(z) = a0zn + a1zn 1 + + an 1z + an è g(z) = b0zm + b1zm 1 + + bm 1z + bm называются равными, åñëè m = n
и коэффициенты при одинаковых степенях z совпадают: a0 = b0, . . . , an = bn.
25
Определим операции сложения и умножения многочленов. Чтобы сложить два многочлена, нужно в выражении
f(z) + g(z) = (a0zn + a1zn 1 + : : : + an) + (b0zm + b1zm 1 + : : : + bm)
привести подобные члены, представив его как некоторый новый многочлен. Чтобы вычислить произведение многочленов f(z), g(z), нужно раскрыть
скобки по обычным правилам и в полученном выражении привести подобные:
f(z)g(z) = (a0zn + a1zn 1 + : : : + an)(b0zm + b1zm 1 + : : : + bm) = = a0b0zm+n + (a0b1 + a1b0)zm+n 1 + : : : + anbm:
Заметим, что степень произведения многочленов равна сумме степеней сомножителей.
Теорема 2.2. (о делении многочленов с остатком) Для любых многочленов f(z) и g(z) существуют многочлены h(z) и r(z), такие, что
f(z) = g(z) h(z) + r(z);
причем степень остатка r(z) строго меньше степени делителя g(z). Много- члены h(z) и r(z) определяются единственным образом.
Если деление выполняется без остатка, т. е. остаток равен 0, то говорят, что многочлен f(z) делится на многочлен g(z)
f(z) = g(z) h(z):
Пример 2.11. Разделить многочлен f(z) на многочлен g(z), если:
1)f(z) = z5 3z4 + z3 + 2z2 5z + 1, g(z) = z2 + z + 2;
2)f(z) = 2z4 z3 + 2z 3, g(z) = z 1;
3)f(z) = 3z3 7z2 + 2z, g(z) = z2 + 1.
Решение.
1) Выполним деление многочлена f(z) на многочлен g(z):
26
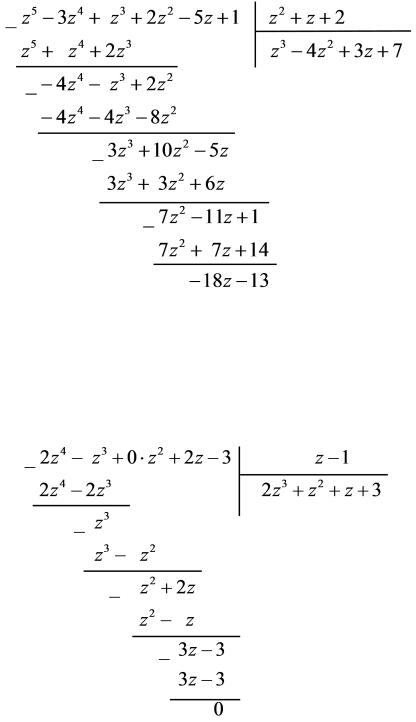
Получаем, что
z5 3z4 + z3 + 2z2 5z + 1 = (z2 + z + 2)(z3 4z2 + 3z + 7) + ( 18z 13):
2) Выполним деление многочлена f(z) на многочлен g(z):
Значит, 2z4 z3 + 2z 3 = (z 1)(2z3 + z2 + z + 3):
3) Выполним деление многочлена f(z) на многочлен g(z):
27
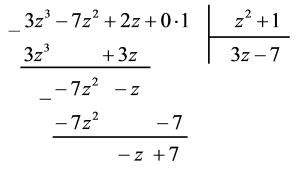
Таким образом, 3z3 7z2 + 2z = (z2 + 1)(3z 7) + ( z + 7): 
Заметим, что константа C 6= 0 является делителем любого многочлена.
Пример 2.12. Многочлен 2z + 7 делится на 5, потому что
2z + 7 = 5 |
5z + |
5 |
: |
|
|
2 |
|
7 |
|
2.5 Корни многочлена. Разложение на множители. Определение 2.9. Число a называется корнем многочлена f(z), если
f(a) = 0:
Корни многочлена могут быть как действительными, так и комплексными.
Пример 2.13. Число 5 является корнем многочлена z3 + 5z2 z 5, ò. ê.
( 5)3 + 5 ( 5) ( 5) 5 = 0.
Пример 2.14. Число i является корнем многочлена z3 + 3z2 + z + 3, ò. ê. i3 + 3 i2 + i + 3 = i2 i + 3 ( 1) + i + 3 = i 3 + i + 3 = 0. Число 2 не является корнем многочлена z3 +3z2 +z+3, ò. ê. 23 +3 22 +2+3 = 8+12+2+3 = 25 6= 0.
Теорема 2.3. (теорема Безу) Остаток от деления f(z) на многочлен z a
равен числу f(a).
Следствие. Если a корень f(z), то f(z) делится на z a без остатка.
Пример 2.15. Проверить, что комплексное число z0 = 2 + i является корнем многочлена f(z) = z3 5z2 + 9z 5 и разделить f(z) на z z0.
28
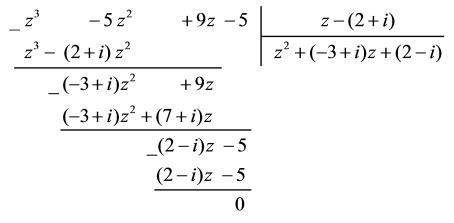
Решение. Проверим, что z0 = 2 + i является корнем многочлена f(z). Получа- ем, что f(2 + i) = (2 + i)3 5(2 + i)2 + 9(2 + i) 5 = 8 + 3 22 i + 3 2 i2 + i3
5(4 + 4i + i2) + 18 + 9i 5 = 8 + 12i 6 i 20 20i + 5 + 18 + 9i 5 = 0.
Теперь разделим f(z) на многочлен z (2 + i):
Таким образом, остаток от деления равен нулю и z3 5z2 + 9z 5 делится на z (2 + i). 
Пусть a корень многочлена f(z). Тогда f(z) = (z a)f1(z).
Определение 2.10. Если a не является корнем многочлена f1(z), то a называется простым корнем f(x).
Если a является корнем многочлена f1(z), òî f1(z) = (z a)f2(z) и, значит, f(z) = (z a)2f2(z).
Определение 2.11. Натуральное число k такое, что f(z) = (z a)kfk(z), ãäå fk(a) 6= 0 называется кратностью корня a.
Говорят, что в этом случае многочлен f(z) имеет k одинаковых корней a.
Пример 2.16. Определить кратность корня z = z0 для многочлена f(z), если:
1)f(z) = z3 4z2 7z + 10, z0 = 1;
2)f(z) = z4 + 6z3 3z2 56z 48, z0 = 4.
Решение.
1) Выполним деление многочлена z3 4z2 7z + 10 на многочлен z 1:
29
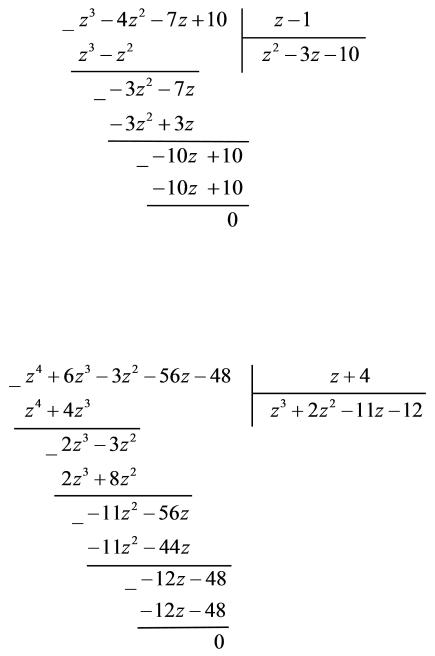
Получаем, что f1(z) = z2 3z 10 è f(1) = 12 3 1 10 = 12 6= 0. Значит, z0 = 1 простой корень.
2) Выполним деление многочлена z4 + 6z3 3z2 56z 48 на многочлен z + 4:
Следовательно, f1(z) = z3 + 2z2 11z 12 è
f1( 4) = ( 4)3 + 2( 4)2 11( 4) 12 = 0:
Теперь делим f1(z) íà z + 4:
30
