
- •2. Линейные операции над векторами.
- •1) Сложение векторов.
- •2. Вычитание векторов.
- •3. Умножение векторов
- •Математически верная формулировка
- •Вопрос №16. Взаимное расположение прямых и плоскостей. Точка пересечения прямой и плоскости.
- •Первый замечательный п на прямой, то векторы редел
- •Теорема о замене функции на эквивалентную под знаком предела
Первый замечательный п на прямой, то векторы редел
![]()
Доказательство

Рассмотрим односторонние
пределы![]() и
и![]() и
докажем, что они равны 1.
и
докажем, что они равны 1.
Пусть
![]() .
Отложим этот угол на единичной окружности
(R= 1).
.
Отложим этот угол на единичной окружности
(R= 1).
Точка K— точка пересечения луча с окружностью, а точкаL— с касательной к единичной окружности в точке (1;0). ТочкаH— проекция точкиKна осьOX.
Очевидно, что:
![]() (1)
(1)
(где SsectOKA— площадь сектораOKA)
![]()
![]()
![]()
(из
![]() :
|LA| = tgx)
:
|LA| = tgx)
Подставляя в (1), получим:
![]()
Так как при
![]() :
:
![]()
У![]() множаем
на sinx:
множаем
на sinx:
П![]()
![]() ерейдём
к пределу:
ерейдём
к пределу:
![]()
Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Вопрос № 27 Второй замечательный предел
Второй замечательный предел:
![]()
![]()
![]()
или
Доказательство второго замечательного предела:
Зная, что второй замечательный
предел верен для натуральных значений
x, докажем второй замечательный предел
для вещественных x, то есть докажем, что
![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:
1. Пусть
![]() .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами:![]() ,
где
,
где![]() —
это целая часть x.
—
это целая часть x.
Отсюда следует:
![]() ,
поэтому
,
поэтому
 .
.
Если
![]() ,
то
,
то![]() .
Поэтому, согласно пределу
.
Поэтому, согласно пределу![]() ,
имеем:
,
имеем:
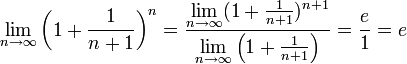
![]() .
.
По признаку (о пределе промежуточной
функции) существования пределов
![]() .
.
2. Пусть
![]() .
Сделаем подстановку −x=t, тогда
.
Сделаем подстановку −x=t, тогда
![]()
![]() .
.
Из двух этих случаев вытекает,
что
![]() для
вещественного x.
для
вещественного x.
Вопрос № 28
СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ
Пусть при x→aфункцииf(x)иg(x)являются бесконечно малыми. Тогда будем пользоваться следующими определениями.
Если
 ,
тоf(x)называетсябесконечно
малой высшего порядка, чемg(x)(относительноg(x)).
,
тоf(x)называетсябесконечно
малой высшего порядка, чемg(x)(относительноg(x)).Если
 ,
то функцииf(x)иg(x)называютсябесконечно малыми одногопорядка.
,
то функцииf(x)иg(x)называютсябесконечно малыми одногопорядка.Если
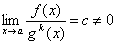 ,
тоf(x)называетсябесконечно
малой k-го порядка относительноg(x).
,
тоf(x)называетсябесконечно
малой k-го порядка относительноg(x).
Если
![]() ,
то функцииf(x)иg(x)называютсяэквивалентными бесконечномалыми.
В этом случае обе функции стремятся к
нулю примерно с одинаковой скоростью.
Эквивалентные бесконечно малые будем
обозначатьf ≈ g.
,
то функцииf(x)иg(x)называютсяэквивалентными бесконечномалыми.
В этом случае обе функции стремятся к
нулю примерно с одинаковой скоростью.
Эквивалентные бесконечно малые будем
обозначатьf ≈ g.
Теорема о замене функции на эквивалентную под знаком предела
Под знаком предела

числитель или знаменатель можно заменить на эквивалентные.Доказательство. Пусть в точкех = х0имеемf(x) ~ α(x). В этом случае
![]() ,
,
что и требовалось доказать.
Вопрос №29 Эквивалентность , связанная с первым заметательным пределом.
Как показывает приведённый выше пример
2.36, пределы отношения бесконечно
малых можно упрощать, откидывая бесконечно
малые слагаемые большего порядка и
заменяя множители в числителе и
знаменателе на эквивалентные бесконечно
малые. Для того, чтобы этот способ
вычисления пределов (точнее, раскрытия
неопределённостей вида![]() )
можно было применять к возможно большему
числу примеров, мы должны иметь достаточно
большой запас известных пар эквивалентных
бесконечно малых величин. Для наиболее
употребительной базы
)
можно было применять к возможно большему
числу примеров, мы должны иметь достаточно
большой запас известных пар эквивалентных
бесконечно малых величин. Для наиболее
употребительной базы![]() создадим
такой запас в виде таблицы "стандартных"
эквивалентных бесконечно малых.
создадим
такой запас в виде таблицы "стандартных"
эквивалентных бесконечно малых.
Поскольку в этой таблице мы
всегда будем рассматривать базу
![]() ,
для простоты записи обозначение этой
базы будем пропускать и писать знак
,
для простоты записи обозначение этой
базы будем пропускать и писать знак![]() вместо
вместо![]() .
.
1)
![]() .
Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность
.
Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность![]() и
и![]() при
при![]() означает
в точности, что первый замечательный
предел равен 1.
означает
в точности, что первый замечательный
предел равен 1.
2)
![]() .
Эта эквивалентность тоже была доказана
выше в одном из примеров.
.
Эта эквивалентность тоже была доказана
выше в одном из примеров.
3)
![]() .
Докажем эту эквивалентность:
.
Докажем эту эквивалентность:

4)
![]() .
Докажите это в качестве упражнения,
сделав замену
.
Докажите это в качестве упражнения,
сделав замену![]() и
применив предыдущую табличную формулу.
и
применив предыдущую табличную формулу.
5)
 .
Для доказательства воспользуемся
формулой
.
Для доказательства воспользуемся
формулой![]() .
Далее, имеем:
.
Далее, имеем:

Это означает, что доказываемая эквивалентность имеет место.
6)
![]() (
(![]() ).
Для доказательства этой эквивалентности
сделаем такое преобразование:
).
Для доказательства этой эквивалентности
сделаем такое преобразование:

Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:
![]()
и мы доказали формулу 6.
В частном случае, при
![]() ,
получаем эквивалентность
,
получаем эквивалентность
![]() )
)![]() .
.
7)
![]() (
(![]() ).
Для доказательства сделаем замену
).
Для доказательства сделаем замену![]() и
выразим
и
выразим![]() через
через![]() :
:![]() .
Согласно формуле 6,
.
Согласно формуле 6,![]() при
при![]() ,
откуда
,
откуда![]() .
Из непрерывности логарифма следует,
что
.
Из непрерывности логарифма следует,
что![]() и,
значит,
и,
значит,![]() при
при![]() .
В этой формуле осталось лишь сменить
обозначение переменного
.
В этой формуле осталось лишь сменить
обозначение переменного![]() на
на![]() ,
чтобы получить формулу 7.
,
чтобы получить формулу 7.
В частном случае, при
![]() ,
получаем эквивалентность
,
получаем эквивалентность
![]() )
)![]() .
.
При
![]() .
.
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
|
5) |
|
|
6) |
|
|
|
|
|
7) |
|
|
|
|
Вопрос №31 Непрерывность функции в точке.
![]() Определение.Функцияf(x),
определенная в окрестности некоторой
точки х0, называетсянепрерывной
в точке х0, если предел функции
и ее значение в этой точке равны, т.е.
Определение.Функцияf(x),
определенная в окрестности некоторой
точки х0, называетсянепрерывной
в точке х0, если предел функции
и ее значение в этой точке равны, т.е.
Тот же факт
можно записать иначе:
![]()
Определение.Если функцияf(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называетсяразрывнойфункцией, а точка х0– точкой разрыва.
П ример
непрерывной функции:
ример
непрерывной функции:
y
f(x0)+
f(x0)
f(x0)-
0 x0- x0 x0+ x
Пример разрывной функции:
 y
y
f(x0)+
f(x0)
f(x0)-x0x

![]() Определение.Функцияf(x)
называется непрерывной в точке х0,
если для любого положительного числа>0 существует такое
число>0, что для
любых х, удовлетворяющих условию
Определение.Функцияf(x)
называется непрерывной в точке х0,
если для любого положительного числа>0 существует такое
число>0, что для
любых х, удовлетворяющих условию
верно неравенство .
Определение.Функцияf(x) называетсянепрерывнойв точке х = х0, если приращение функции в точке х0является бесконечно малой величиной.
f(x) =f(x0) +(x)
где (х) – бесконечно малая при хх0.
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций
![]() –
есть непрерывная функция при условии,
чтоg(x) не
равна нулю в точке х0.
–
есть непрерывная функция при условии,
чтоg(x) не
равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u=f(x),v=g(x) – непрерывные функции в точке х = х0, то функцияv=g(f(x)) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
Непрерывность некоторых элементарных функций.
1) Функция f(x) =C,C=const– непрерывная функция на всей области определения.
2) Рациональная функция
 непрерывна
для всех значений х, кроме тех, при
которых знаменатель обращается в ноль.
Таким образом, функция этого вида
непрерывна на всей области определения.
непрерывна
для всех значений х, кроме тех, при
которых знаменатель обращается в ноль.
Таким образом, функция этого вида
непрерывна на всей области определения.
3) Тригонометрические функции непрерывны на своей области определения.
Докажем свойство 3 для функции y=sinx.
Запишем приращение функции y=sin(x+x) –sinx, или после преобразования:
![]()
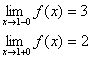
Действительно,
имеется предел произведения двух функций
![]() и
и
![]() .
При этом функция косинус – ограниченная
функция прих0
.
При этом функция косинус – ограниченная
функция прих0
![]() ,
а т.к.
,
а т.к.
предел функции
синус
![]() ,
то она является бесконечно малой прих0.
,
то она является бесконечно малой прих0.
Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция у – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у =sinx– непрерывная функция для любого значения х = х0из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.
Аналогично можно доказать непрерывность остальных тригонометрических функций на всей области определения.
Вообще следует заметить, что все основные элементарные функции непрерывны на всей своей области определения.
Вопрос №32 Определение точек разрыва и их классифифкация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел (см. выше)
![]() ,
то функция называется непрерывной
справа.
,
то функция называется непрерывной
справа.
|
|
|
|
|
|
х0
Если односторонний предел (см. выше)
![]() ,
то функция называется непрерывной
слева.
,
то функция называется непрерывной
слева.
|
|
|
|
|
|
х0
Определение.Точка х0называетсяточкой разрыва функцииf(x), если f(x) не определена в точке х0или не является непрерывной в этой точке.
Определение.Точка х0называетсяточкой разрыва 1- го рода, если в этой точке функцияf(x) имеет конечные, но не равные друг другу левый и правый пределы.
![]()
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение.Точка х0называетсяточкой разрыва 2 – го рода, если в этой точке функцияf(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Вопрос №33 Свойства функций, непрерывных в точке
Поскольку точки
![]() непрерывности
функции
непрерывности
функции![]() задаются
условием
задаются
условием![]() ,
то часть свойств функций, непрерывных
в точке
,
то часть свойств функций, непрерывных
в точке![]() ,
следует непосредственно из свойств
пределов. Сформулируем их в виде следующей
теоремы.
,
следует непосредственно из свойств
пределов. Сформулируем их в виде следующей
теоремы.
Теорема 3.1Пусть функции
![]() и
и![]() непрерывны
в точке
непрерывны
в точке![]() .
Тогда функции
.
Тогда функции![]() ,
,![]() ,
,![]() непрерывны
в точке
непрерывны
в точке![]() .
Если
.
Если![]() ,
то функция
,
то функция также
непрерывна в точке
также
непрерывна в точке![]() .
.
Предложение 3.3Рассмотрим множество всех функций,
определённых в некоторой фиксированной
окрестности
![]() точки
точки![]() и
непрерывных в этой точке. Тогда это
множество
и
непрерывных в этой точке. Тогда это
множество![]() является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
![]()
Доказательство.
Действительно, постоянные![]() и
и![]() --
это непpеpывные функции (в любой точке);
по пpедыдущей теоpеме тогда непpеpывны
в точке
--
это непpеpывные функции (в любой точке);
по пpедыдущей теоpеме тогда непpеpывны
в точке![]() пpоизведения
пpоизведения![]() и
и![]() .
Но тогда по этой же теоpеме непpеpывна в
точке
.
Но тогда по этой же теоpеме непpеpывна в
точке![]() и
сумма
и
сумма![]() .
.
Теорема 3.2Пусть функции f и
,g таковы, что существует
композиция
![]() ,
,![]() .
Пусть функция
.
Пусть функция![]() непрерывна
в точке
непрерывна
в точке![]() ,
а функция
,
а функция![]() непрерывна
в соответствующей точке
непрерывна
в соответствующей точке![]() .
Тогда композиция
.
Тогда композиция![]() непрерывна
в точке
непрерывна
в точке![]() .
.
Доказательство.
Заметим, что равенство![]() означает,
что при
означает,
что при![]() будет
будет![]() .
Значит,
.
Значит,
![]()
(последнее равенство следует из
непрерывности функции
![]() в
точке
в
точке![]() ).
Значит,
).
Значит,
![]()
а это равенство означает, что композиция
![]() непрерывна
в точке
непрерывна
в точке![]() .
.
Заметим, что, очевидно, в
предыдущих двух теоремах можно было бы
заменить базу
![]() на
односторонние базы
на
односторонние базы![]() или
или![]() и
получить аналогичные утверждения для
непрерывности слева или справа:
и
получить аналогичные утверждения для
непрерывности слева или справа:
Теорема 3.3Пусть функции
![]() и
и![]() непрерывны
слева (справа) в точке
непрерывны
слева (справа) в точке![]() .
Тогда функции
.
Тогда функции![]() ,
,![]() ,
,![]() непрерывны
слева (соотв. справа) в точке
непрерывны
слева (соотв. справа) в точке![]() .
Если
.
Если![]() ,
то функция
,
то функция также
непрерывна слева (спpава) в точке
также
непрерывна слева (спpава) в точке![]() .
.
 Теорема
3.4Пусть функция
Теорема
3.4Пусть функция
![]() непрерывна
слева (справа) в точке
непрерывна
слева (справа) в точке![]() ,
а функция
,
а функция![]() непрерывна
в точке
непрерывна
в точке![]() .
Тогда композиция
.
Тогда композиция![]() непрерывна
слева (соотв. справа) в точке
непрерывна
слева (соотв. справа) в точке![]() .
.


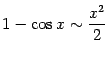 .
.
