
- •Вариант 1.
- •Вариант 2.
- •Вариант 3.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 7.
- •Вариант 8.
- •Вариант 9.
- •Вариант 10.
- •Вариант 11.
- •Вариант 12.
- •Вариант 13.
- •Вариант 14.
- •Вариант 15.
- •Вариант 16.
- •Вариант 17.
- •Вариант 18.
- •Вариант 19.
- •Вариант 20.
- •Вариант 21.
- •Вариант 22.
- •Вариант 23.
- •Вариант 24.
- •Вариант 25.
- •Вариант 26.
- •Вариант 27.
- •Вариант 28.
Вариант 1.
1. Доказать (указать
![]() ),
что
),
что
![]() .
.
2. Вычислить пределы числовых последовательностей:
а)
![]() ;
;
б)
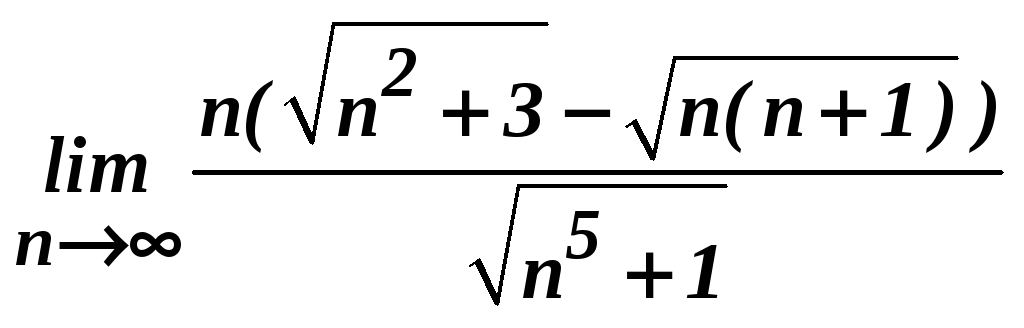 ;
;
в)
![]() ;
;
г)
 ;
;
д)
![]() .
.
3
2
![]() и
и
![]() и при стремлении аргумента функции к
и при стремлении аргумента функции к
![]() .
.
–3
2
–2
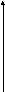


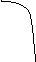
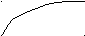




![]()



![]()
![]()
4. Построить
график функции
![]() ,
если известно, что
,
если известно, что
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Дать каждому из пределов определение по Гейне (в терминах пределов последовательностей) и по Коши (используя понятие окрестности).
5. Исследовать функцию на непрерывность, указать характер точек разрыва. Найти асимптоты графика функции. Построить график функции:
а)
![]() ;
б)
;
б)![]() .
.
6. Доказать (найти
![]() ),
что
),
что
а)
![]() ; б)
; б)
![]() .
.
7. При каких значениях
![]() и
и
![]() величины
величины
![]() и
и
![]() при
при
![]() являются бесконечно малыми: а) одного
и того же порядка; б) эквивалентными; в)
одна из них является бесконечно малой
более высокого порядка, чем другая?
являются бесконечно малыми: а) одного
и того же порядка; б) эквивалентными; в)
одна из них является бесконечно малой
более высокого порядка, чем другая?
8. Сравнить бесконечно
малые при
![]() величины
величины
![]() и
и
![]() .
.
9. Вычислить пределы функций:
а)
![]() ; б)
; б)
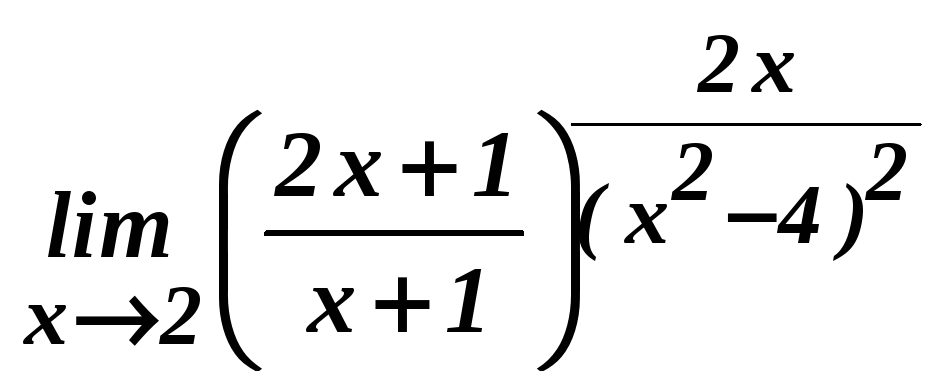 ;
;
в)
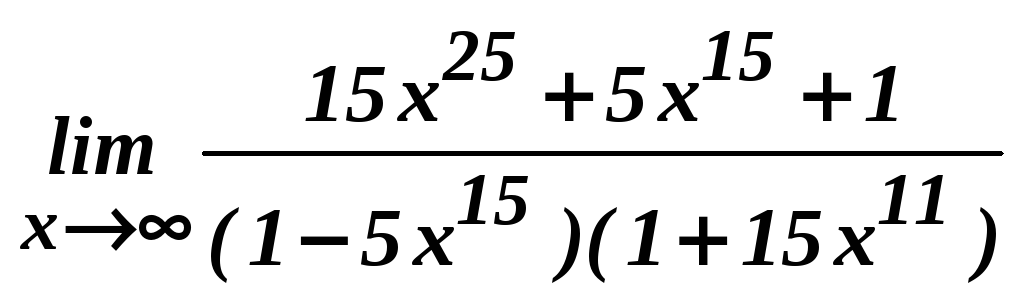 ; г)
; г)
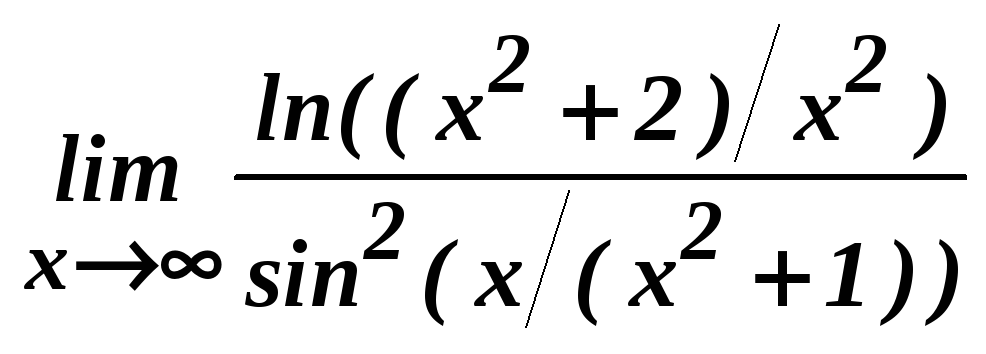 ;
;
д)
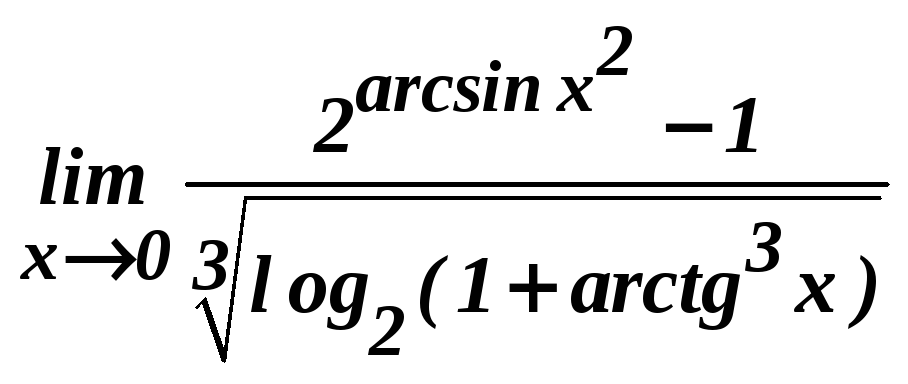 ; е)
; е)
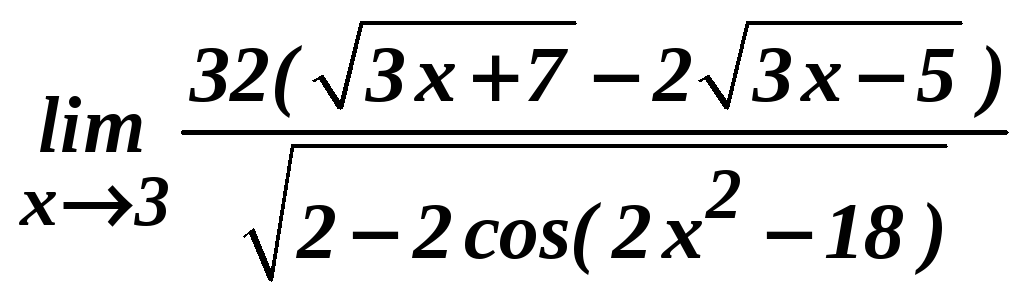 ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
10. Найти постоянные a и b из условия
![]()
Вариант 2.
1. Доказать (указать
![]() ),
что
),
что
![]() .
.
2. Вычислить пределы числовых последовательностей:
а)
![]() ;
б)
;
б)
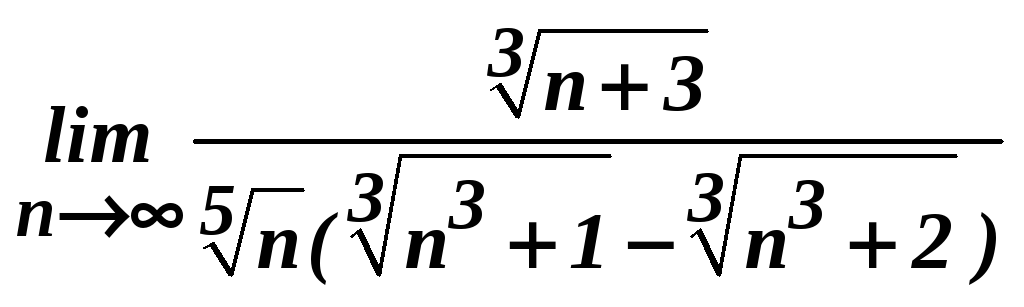 ;
;
в)
![]() ;
г)
;
г)
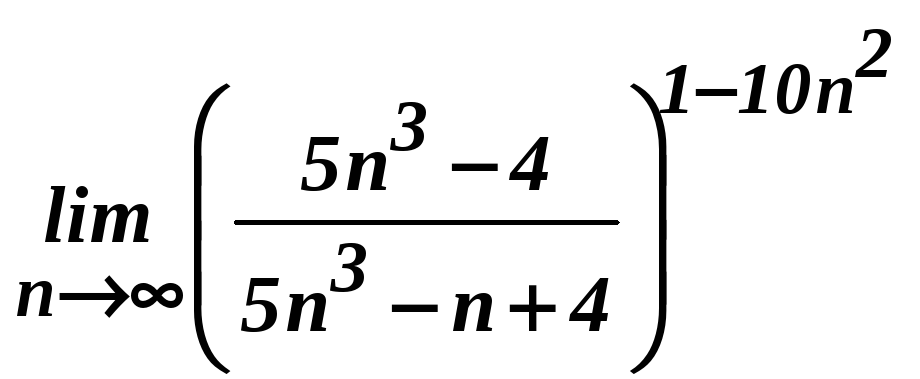 ;
;
д)
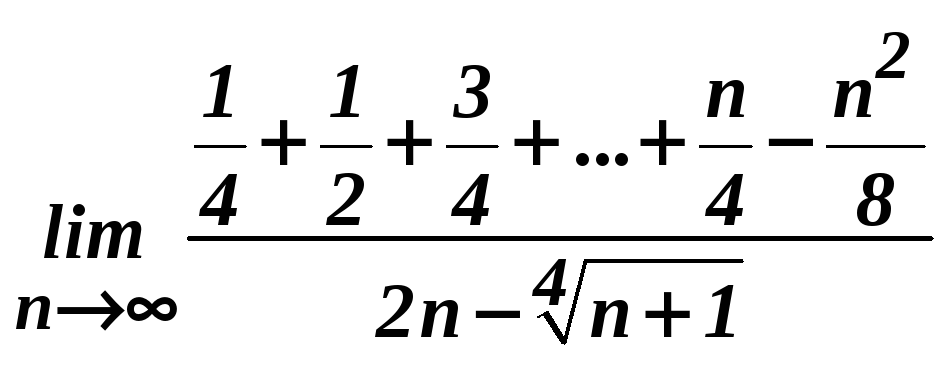 .
.
3. По
эскизу графика описать поведение функции
на языке пределов в точках
![]() и
и
![]() и при стремлении аргумента функции к
и при стремлении аргумента функции к
![]() .
.
–1
2 –3








![]()


![]()
![]()
4. Построить
график функции
![]() ,
если известно, что
,
если известно, что
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Дать каждому из пределов определение по Гейне (в терминах пределов последовательностей) и по Коши (используя понятие окрестности).
5. Исследовать
функцию на непрерывность, указать
характер точек разрыва. Найти асимптоты
графика функции. Построить график
функции: а)![]() ;
б)
;
б)![]() .
.
6. Доказать (найти
![]() ),
что
),
что
а)
![]() ;
б)
;
б)
![]() .
.
7. При каких значениях
![]() и
и
![]() величины
величины
![]() и
и
![]() при
при
![]() являются бесконечно малыми: а) одного
и того же порядка; б) эквивалентными; в)
одна из них является бесконечно малой
более высокого порядка, чем другая?
являются бесконечно малыми: а) одного
и того же порядка; б) эквивалентными; в)
одна из них является бесконечно малой
более высокого порядка, чем другая?
8. Сравнить бесконечно
малые при
![]() величины
величины
![]() и
и
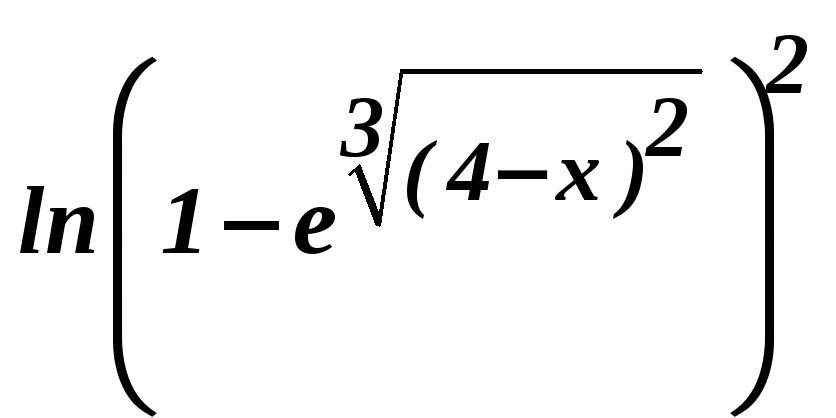 .
.
9. Вычислить пределы функций:
а)
![]() ;
б)
;
б)
 ;
;
в)
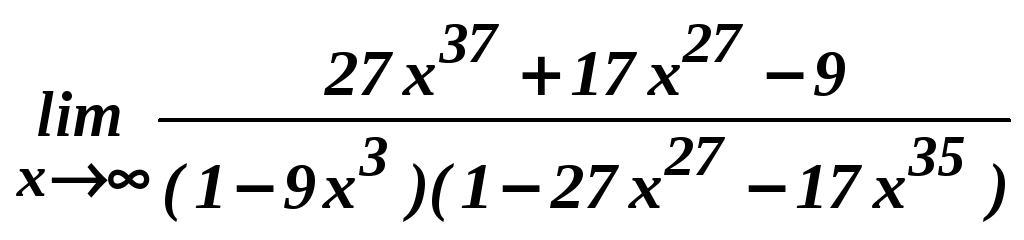 ;
г)
;
г)
![]() ;
;
д)
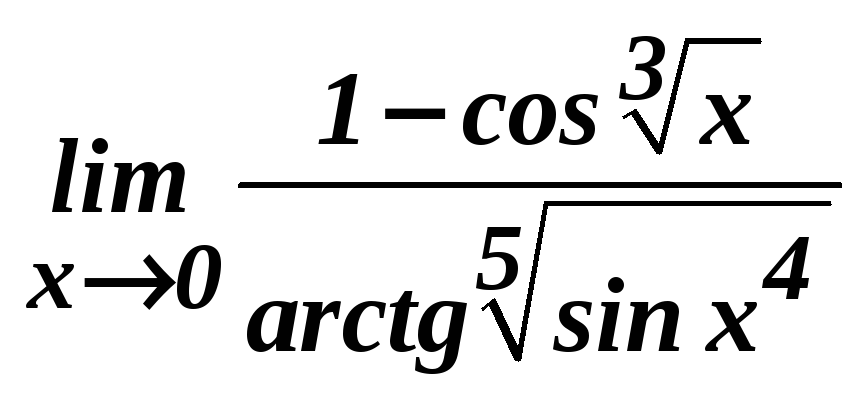 ;
е)
;
е)
![]() ;
;
ж)
![]() ;з)
;з)
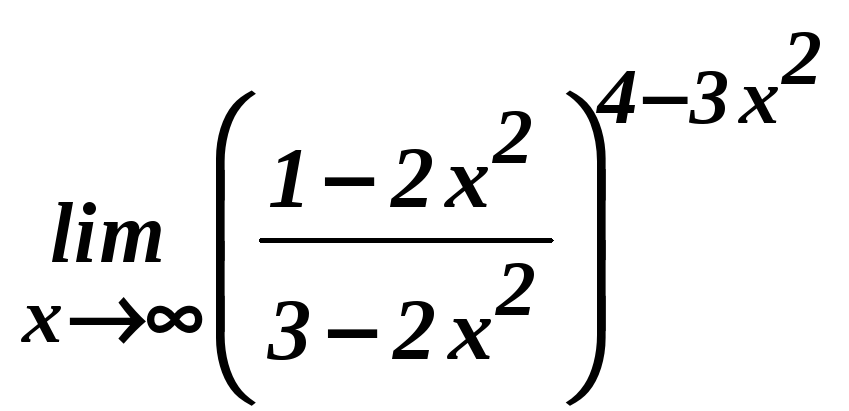 ;
;
и)
![]() .
.
10. Найти постоянные
a
и b
из условия ![]()
Вариант 3.
1. Доказать (указать
![]() ),
что
),
что
![]() .
.
2. Вычислить пределы числовых последовательностей:
а)
![]() ;
;
2![]() ;
;
в)
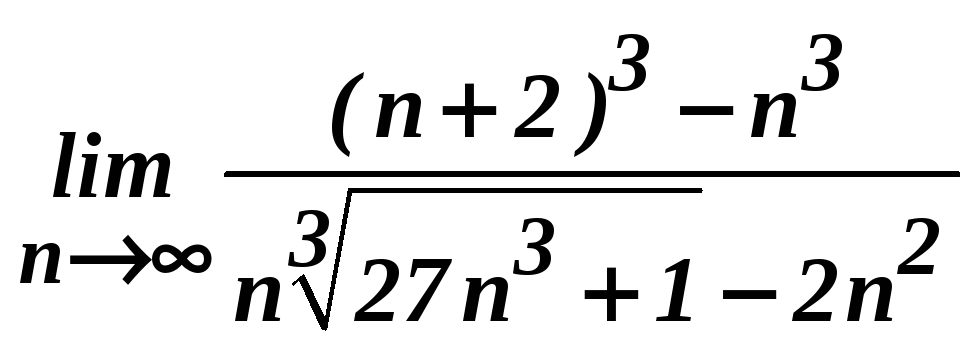 ;
;
г)
 ;
;
4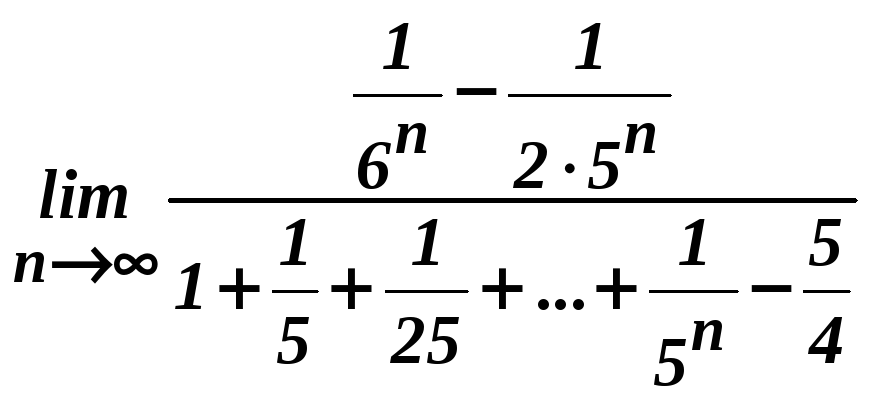 .
.
3. По
эскизу графика описать поведение функции
на языке пределов в точках
![]() и
и
![]() и при стремлении аргумента функции к
и при стремлении аргумента функции к
![]() .
.
–2 –2
3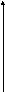






![]()



![]()
![]()
4. Построить
график функции
![]() ,
если известно, что
,
если известно, что
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Дать каждому из пределов определение по Гейне (в терминах пределов последовательностей) и по Коши (используя понятие окрестности).
5. Исследовать
функцию на непрерывность, указать
характер точек разрыва. Найти асимптоты
графика функции. Построить график
функции: а)
![]() ;
б)
;
б)
![]() .
.
6. Доказать (найти
![]() ),
что
),
что
а)
![]() ; б)
; б)
![]() .
.
7. При каких значениях
![]() и
и
![]() величины
величины
![]() и
и
![]() при
при
![]() являются бесконечно малыми: а) одного
и того же порядка; б) эквивалентными; в)
одна из них является бесконечно малой
более высокого порядка, чем другая?
являются бесконечно малыми: а) одного
и того же порядка; б) эквивалентными; в)
одна из них является бесконечно малой
более высокого порядка, чем другая?
8. Сравнить бесконечно
малые при
![]() величины
величины
![]() и
и
![]() .
.
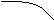
9. Вычислить пределы функций:
а)
![]() ; б)
; б)
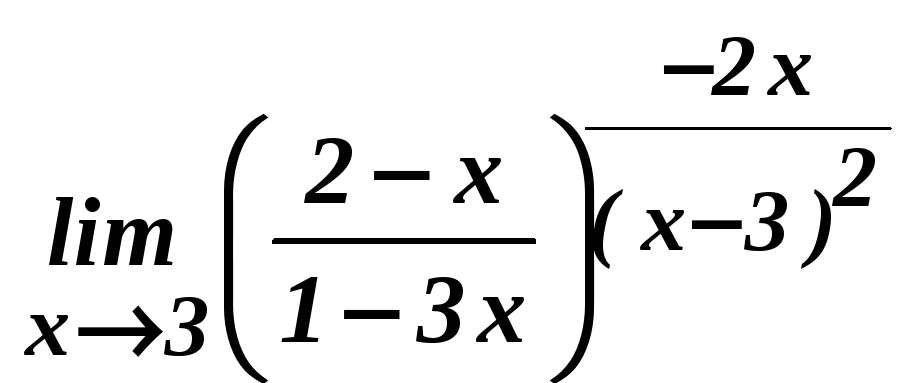 ;
;
в)
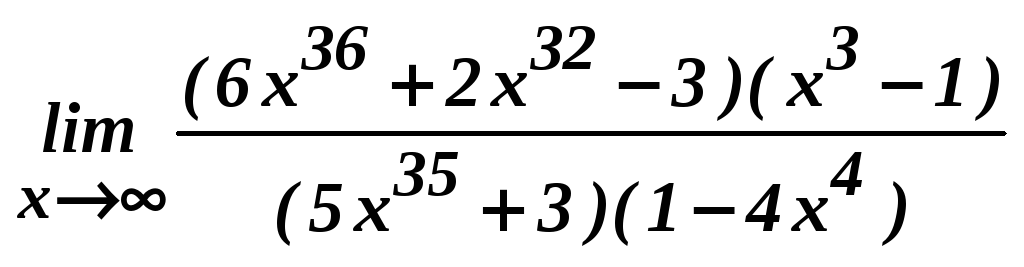 ; г)
; г)
![]() ;
;
д)
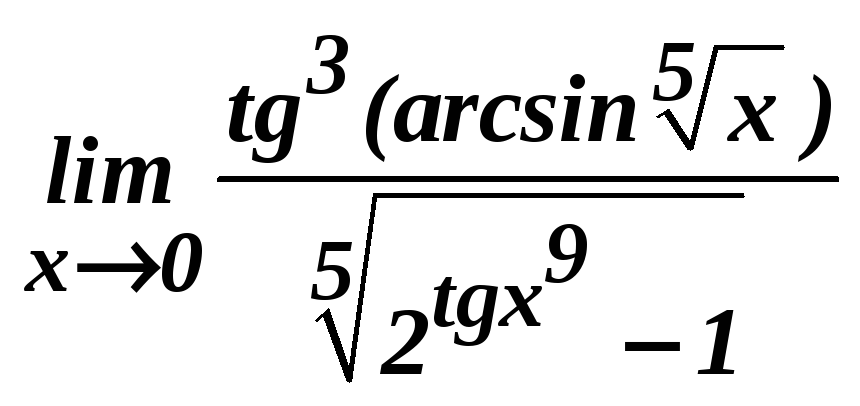 ; е)
; е)
![]() ;
;
ж)![]() ;з)
;з)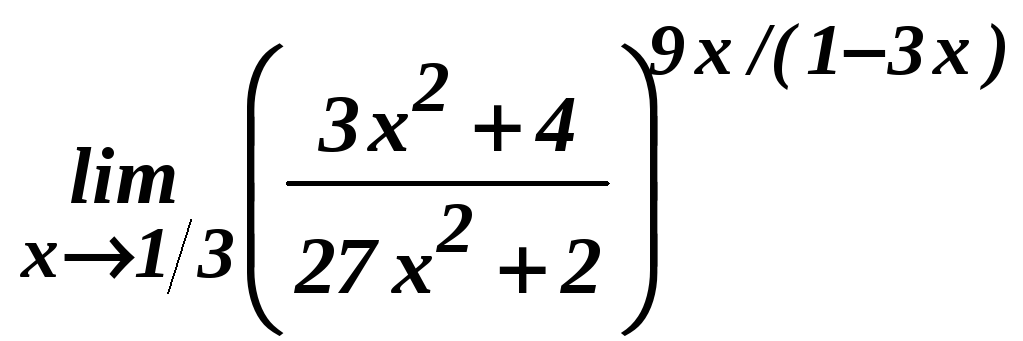 ;
;
и)
![]() .
.
10. Найти постоянные a и b из условия
![]() .
.
