8. Динамический расчет системы методом перемещений.

Порядок расчета:

1. Анализируем схему и выбираем основную систему.

2. Строится изгибающий момент.

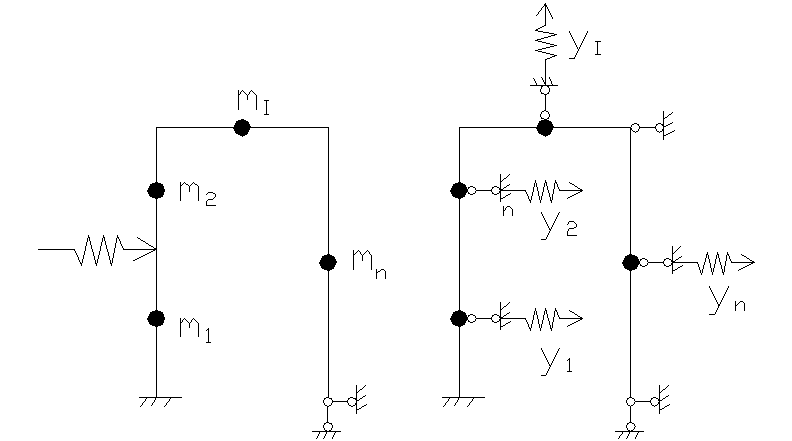
Для заданной системы основная получилась путем введения связей по направлению неизвестных перемещений z₁, z₂ … z_n cсоответствующих масс m₁, m₂ …m_n. число степеней свободы упругой системы определяется числом возможных независимых смещений. Получаем систему уравнений: 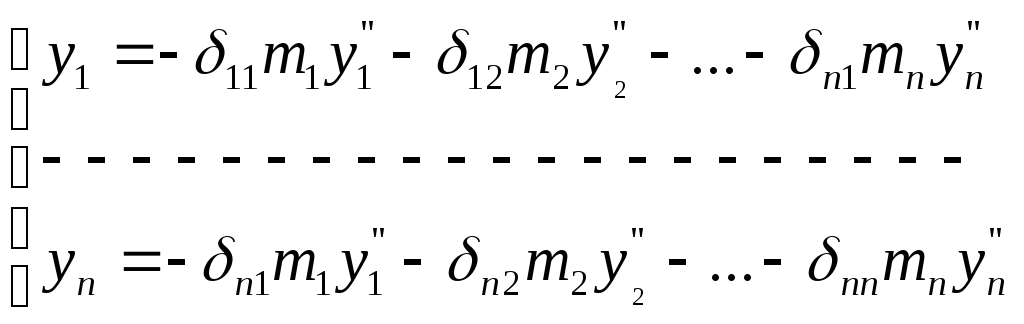(1)

Частное решение системы:

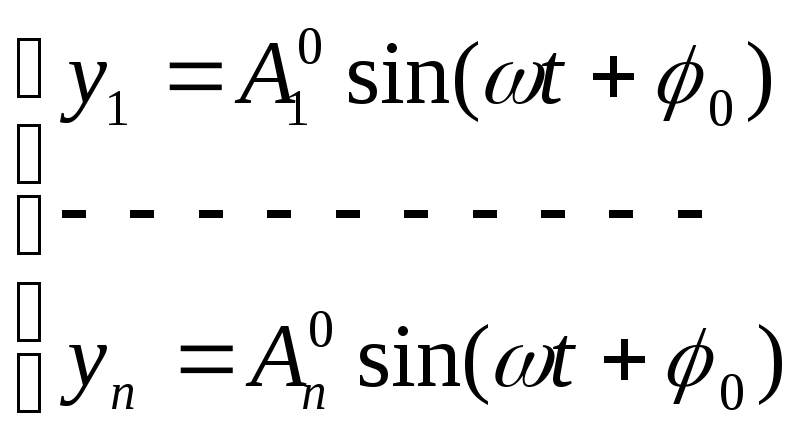(2)

A₁, A_n – амплитуды колебаний соотв. масс, φ₀ – нач. фаза колебаний.

Возьмем вторую производную по времени t:

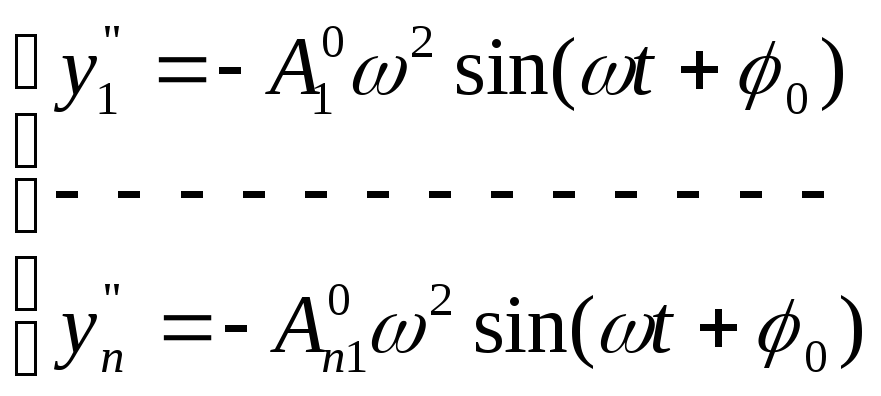(3)

Подставляем из ур-я (3) и (2)в (1):

Перобразовываем:

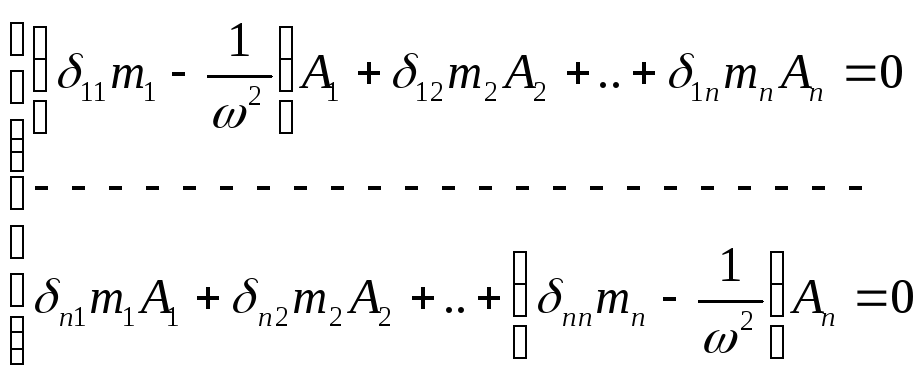
1/ω²=λ

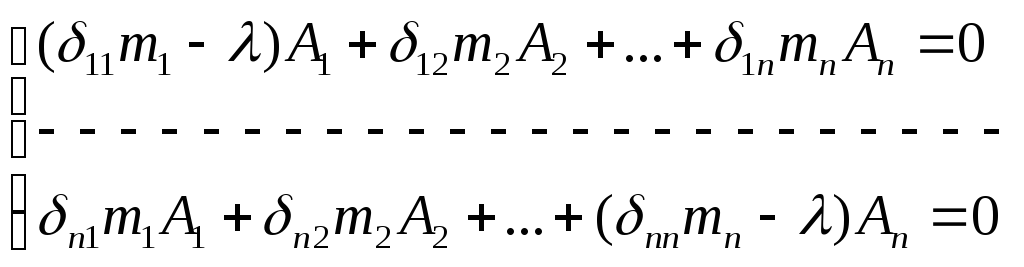
Если А₁=А₂=…=А_n=0 (сист-ма наход. в покое) Если А₁≠А₂≠А_n, тогда когда определитель из коэф-ов при амплитудах=0.

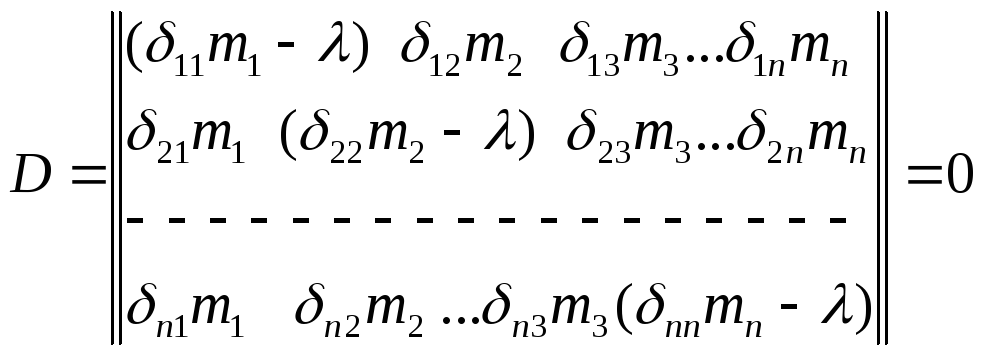
Вековое ур-ие с n-степенью свободы.

Раскрываем полученный определитель. Если вековое уравнение 2-го или 3-го порядка его решение достаточно просто, но при дальнейшем увеличении порядка решение становится затруднительным.

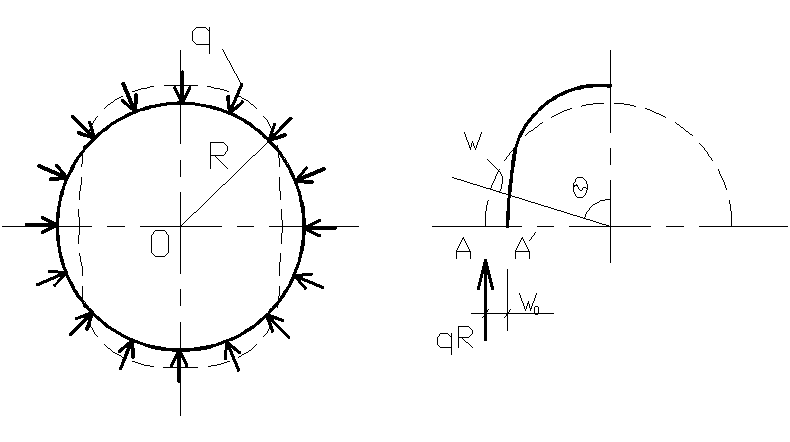
59. Устойчивость кругового кольца при гидростатич. Давлении.

До потери устойчивости все сечения кольца испытывают только сжатие и продольная сила равна N=qR. При достижении нагрузкой критического значения может произойти потеря устойчивости и кольцо примет слегка изогнутую форму, к-ая будет формой равновесия. Рассмотрим изогнутую равновесную форму с двумя осями симметрии. ДУ изгиба бруса кругового очертания: . Изгибающий момент в точке А΄ равенM₀=qRω₀, а изгиб. момент в произвольной точке kM=qRω. Подставляя в ДУ и после небольшого преобразования. обозначив черезполучим общее решение этого однородного диф. уравнения в след. виде.

Граничные условия:

1) при θ=0 откудаB=0;

2) при т.к.ω не обращается тождественно в ноль, следовательно, что дает минимальное значениеn_min=2. Таким образом, минимальная критическая нагрузка, соответ. данной форме потери устойчивости, определяется из условия .

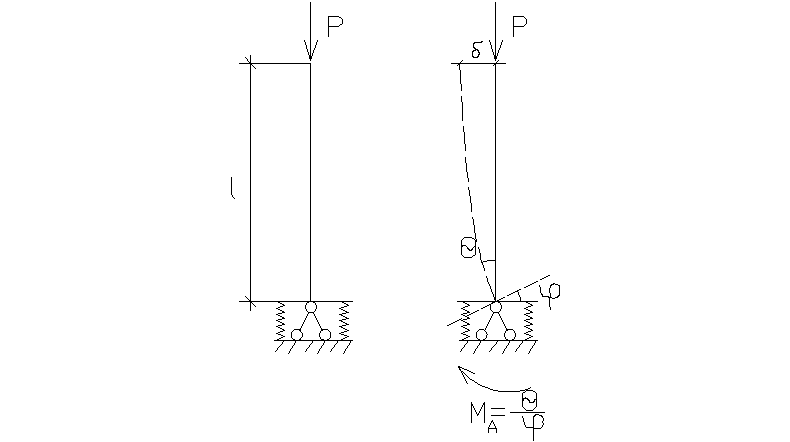
6. Метод исследования устойчивости упругих систем.

В задачах устойчивости используют энергетический и статический метод (есть еще динамический, но он редко применяется). Статический метод – заключается в составлении и интегрировании ДУ равновесия элемента упругой системы, находящейся в таком деформированном состоянии, к-ое отличается от исходного наличием перемещений, вызывающих новый вид деформации.

Энергетический метод – основан на использовании энергетических признаков устойчивого и неустойчивого равновесия упругой системы, согласно к-м система находится состоянии устойчивого равновесия, если ее потенциальная энергия минимальна по сравнению с энергией смежных равновесных. Если ε_р=max, то равновесие устойчиво.

Пример: Определить Р_кр для жесткого стержня. М=1; φ=1 – угол поворота. Стат. метод: ΣМ_А=0 .

Энергетический метод: Выразим изменения упругой системы через работу силы Р. Работа силы Р=А=Pl(1-cosθ)=2Plsin² (θ/φ)=(Plθ²)/2. Работа совершаемая опорным моментом, определяется . Изменение полной упругой энергии. Энергетическим критерием потери устойчивости системы явл. условие:.