32 Потеря устойчивости I рода

При потери устойчивости формы нарушается условие равновесия между внешними и внутренними силами, соответствующими первоначальному виду деформации.. Потерю устойчивости, связанную с разветвлением форм равновесия, называется потерей устойчивости I рода. Характеризуется при постоянном возрастании нагрузки, разрушения прежней формы деформации, качественно отличное от прежней. К таким нарушениям относятся потеря устойчивости центрального сжатия, потеря устойчивости формы деформации, потеря устойчивости плоской формы, потеря устойчивости плоской формы изгиба.

Предельное значение нагрузки при которых становится возможным возникновение деформаций нового типа назначают критическую нагрузку для данного сооружения. Состояние сооружения при котором происходит потеря устойчивости прежней формы деформации называется критическим состоянием I-го рода.

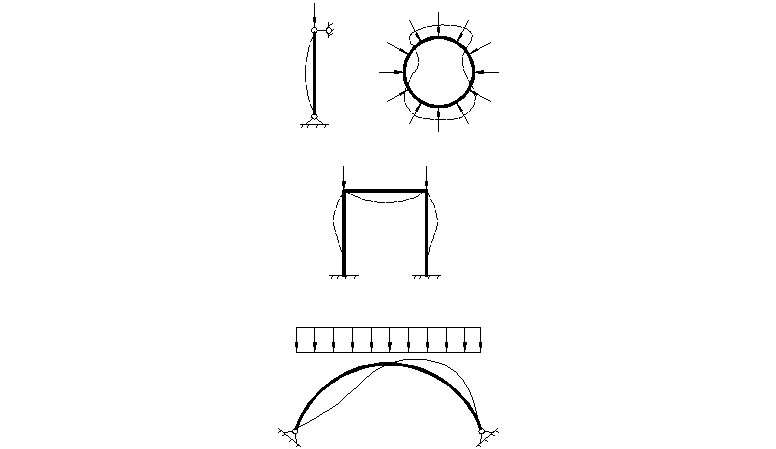
21 Определение частоты колебаний балочной фермы

/

Способ перехода к эквивалентной балки состоит в том, что ферма заменяется балкой сплошного сечения, обладающей жесткостью эквивалентной жесткости фермы и тогда частота колебаний фермы определяется как для балки.

Момент инерции искомой балки определяется из условия равенства прогибов фермы и эквивалентной балке в наибольшей характерной точке – в середине пролета или над точкой приложения наибольшего сосредоточенного груза.

,,

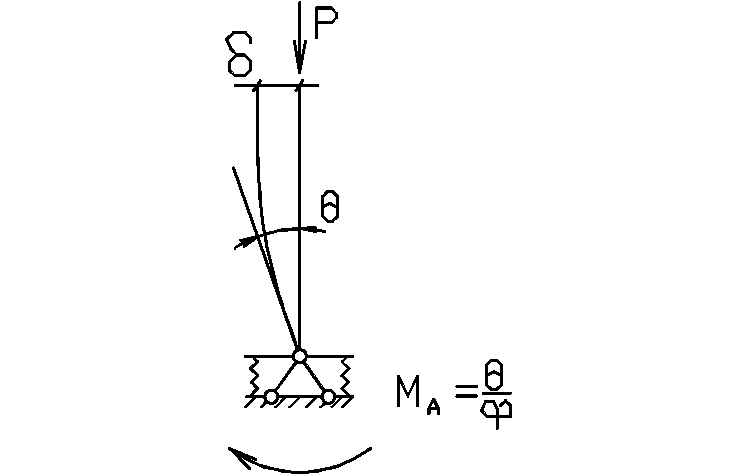
Зная моменты инерции эквивалентной балки можно определить частоту колебаний фермы по формуле:

, ,

,

, ,

Используемые приемы перехода к эквивалентной балки для определения частот колебаний фермы дают удовлетворительные результаты.

24. Устройство стержня с жёсткой заделкой на одном конце и упругой опорой ан другом.

Т.к.

и , а получаем

откуда:

1) при r₁₁=0 (свободный верхний конец) получим , (где i=1,2,3…) и

2) При (жёсткий опорный стержень)

45. Определение коэффицентов при неизвестных метода сил.

Коэффициенты при неизвестных являются переменными основной системы по направлению неизвестных от единичных сил действующих по направлению неизвестных Х₁, Х_2,…Х_n. Свободные члены уравнений - это переменные основной системы по направлению неизвестной от заданной нагрузки.

Коэффициенты при неизвестных и свободных членах уравнений определяют с помощью интеграла Максвелла-Мора:

Предворительно должны быть построены эпюры моментов от единичных нагрузок (сил) и от заданной нагрузки. Где возможно применяют правило Верещагина. Главные коэффициенты всегда положительны, а побочные - положительны, отрицательны и равны 0.

В основной системе как можно большее число побочных перемещений должно быть равно нулю!

4. Энергетический метод исследования устойчивости.

Основан на исследовании энергетических признаков устойчивого и не устойчивого равновесия упругой системы, согласно которым система находится в состоянии устойчивого равновесия, если её потенциальная энергия минимальна по сравнению с энергией смежных равновесных систем.

Если , то равновесие устойчиво.

Пример: Определить Р_кр для жёсткого стержня.

Выразим изменения упругой энергии системы через работу силы Р. Работа силы:

Работа совершаемая опорным моментом, определяется:

Изменение полной упругой энергии:

Энергетическим критерием потери устойчивости системы является условие: