
Lineinaya_algebra_i_analiticheskaya_geometriya
.pdf
61
КОНТРОЛЬНАЯ РАБОТА №1
Задача 1. Решить систему линейных уравнений двумя способами: методом Крамера и матричным методом.
ax 2y z 43x ay 4z b 1x 5y z a b
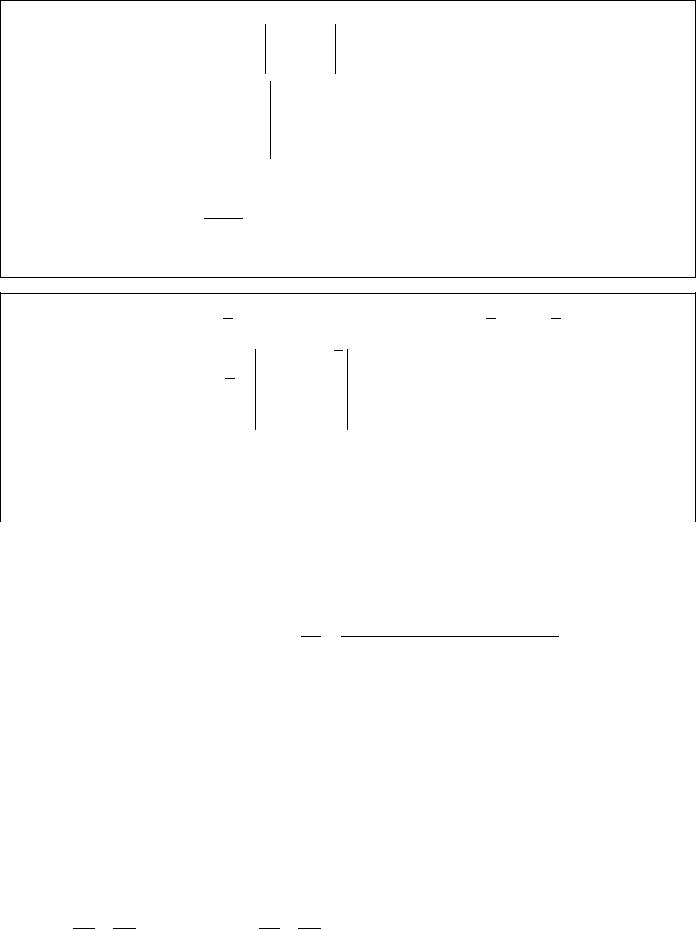
Задача 2. Проверить справедливость равенств (AB) (BA) (A) (B), где
2 |
b |
1 |
|
a |
3 |
0 |
||||
|
1 |
|
|
|
|
|
|
|
|
|
A |
4 |
a |
|
, |
B |
4 |
1 |
2 |
. |
|
|
5 |
1 |
3 |
|
|
|
2 |
1 b |
|
|
|
|
|
|
|
||||||
Задача 3. Даны векторы: a (1;3;a) , b (2;b; 1) , c ( 3;a;b) . Определить, образуют ли векторы a,b,c базис в пространстве R3 . Если да, то разложить вектор d (5;0;4) по этому базису.
Задача 4. Даны вершины пирамиды ABCD : A(2;a 1;0) , B(3;1;b 4) ,
C( 1;5;b a) , D(a;2;3) . Найти:
a)длину ребра BD ;
b)угол между ребрами AB и AC ;
c)площадь грани BCD ;
d)объем пирамиды.
Задача 5. Даны вершины треугольника ABC : A(a;1) ; B(a 1;5) ; C(2;b 6). Найти:
a)уравнение стороны AB ;
b)уравнение высоты AH ;
c)уравнение медианы BM ;
d)точку пересечения высоты AH и медианы BM .
Задача 6. Построить многоугольник и вычислить значения функции z в его вершинах:
x 0, |
|
|
|
|
|
|
|
y 0, |
|
|
z (a 3)x (b 2)y . |
|
|
|
|
y (a 1)x |
2, |
|
|
|
8. |
|
|
(b 2)x |
|
|
|
Задача 7 . Даны точки: A(1;0;a) , |
B(3;b;1) , C( 2;1;a 4) , D(5;2;b a) . Найти: |
||
a)канонические и параметрические уравнения прямой AB ;
b)уравнение плоскости , проходящей через точки A, B и C ;
62
c)параметрические уравнения прямой l , проходящей через точку D перпендикулярно к плоскости ;
d)точку пересечения прямой l и плоскости .
Задача 8. Построить плоскости:
a)x 2y (a 1)z 10 0 ;
b)(b 1)x 4y 12 0 ;
c)3x (b 2)z 0;
d)(a 2)y 15 0 .
Пояснение Числа a и b выбираются студентом по его зачетной книжке (или студенческому билету):
a – это последняя цифра в “зачетке”,
b – это предпоследняя цифра в “зачетке”.
Желаем Вам успехов!
63
Матрицы и определители
Определитель 2го порядка: (A) a11 |
a12 |
a |
a |
22 |
a |
a |
21 |
. |
|
|
|
|||||||
|
|
|
|
|
a21 |
a22 |
11 |
|
12 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
( 1)i k M |
|
|
|||
3го порядка: (A) a |
21 |
a |
22 |
a |
23 |
a |
A |
a |
A |
a |
A |
|
, A |
ik |
. |
|||
|
|
|
11 11 |
12 |
|
12 |
13 13 |
ik |
|
|
||||||||
a31 |
a32 |
a33 |
|
|
An1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
A11 |
A21 |
|
|
|
|
|
|
|
|||||
Обратная матрица: A 1 |
|
1 |
|
A12 |
A22 |
An2 . |
|
|
|
|
|
|
|
|||||
|
|
(A) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
A2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1n |
|
Ann |
|
|
|
|
|
|
|
||||
Векторы
Скалярное произведение: a b a1 b1 a2 b2 an bn , a b 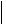 a
a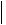
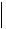 b
b cos .
cos .
|
|
|
|
i |
j |
k |
|
|
|
|
Векторное произведение: a b a1 |
a2 |
a3 . |
|
|
|
|||||
|
|
|
|
b1 |
b2 |
b3 |
|
|
|
|
|
|
|
|
a1 a2 a3 |
|
|
|
|||
Смешанное произведение: ab c b1 |
b2 |
b3 . |
|
|
|
|||||
|
|
|
|
c1 c2 |
c3 |
|
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
Комплексные числа |
|
|||||
Сложение комплексных чисел: |
|
|
z1 z2 x1 x2 i y1 y2 . |
|
||||||
Умножение комплексных чисел: |
|
z1 z2 |
x1x2 y1 y2 i x1 y2 x2 y1 . |
|||||||
Деление двух комплексных чисел: |
z1 |
x1x2 |
y1 y2 i x2 y1 x1 y2 |
, z 0 . |
||||||
|
|
|
|
|
z2 |
|
|
|
x22 y22 |
|
|
|
|
|
|
|
|||||
|
|
|
|
Прямые и плоскости |
|
|||||
Уравнение прямой в R2 : y y |
0 |
k(x x ) , где k tg y2 y1 |
|
|||||||
|
|
|
|
0 |
|
|
|
x2 x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x b1t x0 |
|
|||
|
|
|
|
|
|
|
b2t |
y0 . |
|
|
Параметрические уравнения прямой в R3: y |
|
|||||||||
|
|
|
|
|
|
z |
b t |
z |
0 |
|
|
|
|
|
|
|
|
3 |
|
|
|
Уравнение плоскости: A(x x0 ) B(y y0 ) C(z z0 ) 0 . |
|
|||||||||
|
|
|
|
|
|
|||||
|
|
|
|
Кривые второго порядка |
|
|||||
Эллипс: x2 |
y2 1, гипербола: |
x2 |
y2 |
1; парабола: y2 2 px . |
|
|||||
a2 |
b2 |
|
|
a2 |
b2 |
|
|
|
|
|
