
oin
.pdf6. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
Пусть требуется найти значение какой-либо геометрической или физической величины A (площадь фигуры, объём тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком [a;b] изменения независимой переменной x . Предполагается, что эта
величина A аддитивна, т. е. такая, что при разбиении отрезка [a;b]
точкой c [a;b] на части [a;c] и [c;b] значение величины A ,
соответствующее всему отрезку [a;b] , равно сумме её значений,
соответствующих [a;c] и [c;b]. Для нахождения этой величины A
можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала).
Первая схема базируется на определении определённого интеграла.
1. Точками x0 = a, x1,......xn = b разбить отрезок [a;b] на n частей. В
соответствии с этим, интересующая нас величина A разобьётся на n «элементарных слагаемых» Ai (i = 1,...n) :
A = A1 + A2 + ... + An .
2.Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего
отрезка на его длину: Ai ≈ f (ci ) xi (i = 1,...n) .
При нахождении приближённого значения Ai допустимы некоторые упрощения: дугу на малом участке можно заменить хордой,
11
стягивающей её концы; переменную скорость на малом участке можно приближённо считать постоянной и т. д.
Получим приближённое значение величины A в виде интегральной суммы:
|
n |
A ≈ f (c1 ) x1 + f (c2 ) x2 + ... + f (cn ) xn = ∑ f (ci ) xi . |
|
|
i=1 |
3. Искомая величина A равна пределу интегральной суммы, т. е. |
|
n |
b |
A = lim ∑ f (ci ) |
xi = ∫ f (x)dx . |
n→∞ i=1 |
a |
Указанный «метод сумм», как видим, основан на представлении интеграла как о сумме бесконечно большого числа бесконечно малых слагаемых.
Схема I была применена для выяснения геометрического и физического смысла определённого интеграла.
Схема II представляет собой несколько видоизмененную схему I и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков».
1.На отрезке [a;b] выбираем произвольное значение x и
рассматриваем переменный отрезок [a; x] . На этом отрезке
величина |
A становится функцией x : A = A(x) , т. е. считаем, |
что |
|||
часть искомой величины A есть неизвестная функция A(x) , |
где |
||||
x [a;b] − |
один из параметров величины A ; |
|
|||
2. Находим главную часть приращения |
A при изменении x |
на |
|||
малую величину |
x = dx , т. е. |
находим дифференциал |
dA |
||
функции |
A = A(x) : |
dA = А(x)dx , |
где |
f ( x) , определяемая |
из |
12
условия задачи, функция переменной x (здесь также возможны различные упрощения);
3. Считая, что dA » DA при Dx ® 0 , находим искомую величину путем интегрирования dA в пределах от a до b :
b
A(b) = A = ∫ f (x)dx .
a
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
Прямоугольные координаты
Как уже было установлено площадь криволинейной трапеции, расположенной «выше» оси абсцисс ( f (x) ³ 0 ) (рис. 3), равна соответствующему определённому интегралу:
y y = f ( x)
|
|
|
|
dS |
|
|
|
|
|
S ( x) |
|
|
|
|
|
|
|
dx |
x |
|
|
O a |
x x + dx |
|
|||
|
b |
|
||||
|
|
|
|
Рис. 3 |
|
|
b |
b |
|
|
|||
S = ∫ f (x)dx или S = ∫ y dx |
|
[1] |
||||
a |
a |
|
|
|||
Эта формула получена путём применения схемы I − |
метода сумм. |
|||||
Отметим, что если криволинейная трапеция расположена «ниже» |
||||||
оси Ox ( f (x) < 0 ), то её площадь может быть найдена по формуле |
||||||
|
b |
|
|
|
||
S = −∫ f (x)dx |
|
[2] |
|
|||
|
a |
|
|
|
||
Формулы [1] и [2] можно объединить в одну: |
|
|||||
|
b |
|
|
|
|
|
|
|
|
|
|
||
S = |
∫ f (x)dx |
. |
|
[3] |
|
|
|
a |
|
|
|
|
|
13
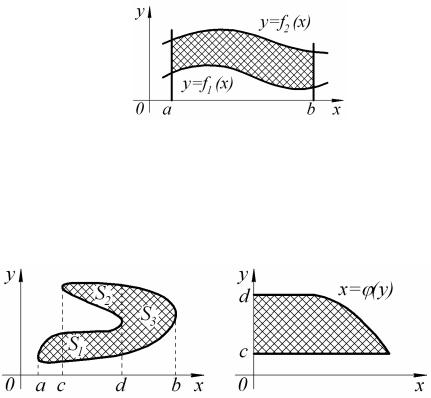
Площадь фигуры, ограниченной кривыми y = f1 (x) и y = f2 (x) ,
прямыми x = a и x = b (при условии f2 (x) ³ f1 (x) ) (рис. 4), можно найти
b b b
по формуле S = ∫ f2 (x)dx − ∫ f1 (x)dx = ∫( f2 (x) − f1 (x))dx .
a a a
Рис. 4
Если плоская фигура имеет «сложную» форму (рис. 5), то прямыми, параллельными оси Oy , её следует разбить на части так,
чтобы можно было бы применить уже известные формулы.
Рис. 5 |
Рис. 6 |
Если криволинейная трапеция ограничена прямыми y = c и y = d , |
|
осью Oy и непрерывной кривой |
x = ϕ( y) ³ 0 (рис. 6), то её площадь |
d
находится по формуле S = ∫ xdy .
c
И, наконец, если криволинейная трапеция ограничена кривой,
|
x = x(t), |
t Î[α ; β ] и прямыми x = a и x = b , |
заданной параметрически |
y = y(t). |
14
|
|
β |
|
и осью Ox , то площадь её находится по формуле S = |
∫ y(t) × x¢(t)dt |
, где |
|
|
|
α |
|
α и β определяются из равенств x(α ) = a и x(β ) = b . |
|
|
|
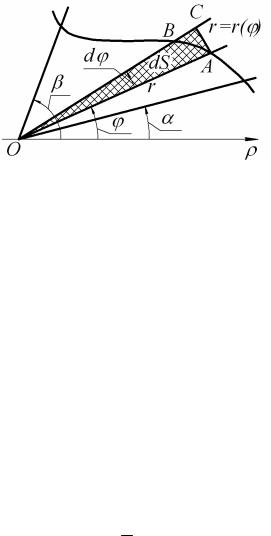
Полярные координаты |
|
|
|
Найдём площадь S |
криволинейного сектора, т. е. плоской |
||
фигуры, ограниченной непрерывной линией r = r(ϕ) |
и двумя лучами |
||
ϕ = a и ϕ = b ( a < b ), где r |
и ϕ − полярные координаты (рис. 7). Для |
||
решения задачи используем схему II − метод дифференциала.
Рис. 7
1. Будем считать часть искомой площади S как функцию угла ϕ , т. е.
S = S (ϕ) , где |
α < ϕ < β |
(если |
ϕ = a , то |
S (α ) = 0 , |
если |
ϕ = b , то |
S (β ) = S ). |
|
|
|
|
|
|
2. Если текущий полярный угол ϕ получит приращение |
ϕ = dϕ , то |
|||||
приращение |
площади |
S |
равно |
площади |
«элементарного |
|
криволинейного сектора» OAB . |
|
|
|
|
||
Дифференциал dS представляет собой главную часть приращения S при dϕ → 0 и равен площади кругового сектора OAC (на рис. 7 она заштрихована) радиуса r с центральным углом dϕ . Поэтому
dS = 1 r 2 × dϕ . 2
15
3. Интегрируя полученное равенство в пределах от ϕ = a до ϕ = b ,
β
получим искомую площадь S = 1 ∫ r2 × dϕ . 2 α
ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ ПЛОСКОЙ КРИВОЙ
Прямоугольные координаты
Пусть в прямоугольных координатах дана плоская кривая AB , уравнение которой у = f (x) , где a < x < b (рис. 8).
Под длиной дуги AB понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена её стремится к нулю.
Рис. 8
Если функция у = f (x) и её производная |
у |
′ |
= f |
′ |
непрерывны |
||
|
(x) |
||||||
на отрезке [a;b] , то кривая AB имеет длину, равную |
|
|
|||||
b |
|
|
|
|
|
||
l = ∫ |
1 + ( f ¢(x))2 |
dx . |
|
|
|
[4] |
|
a
Если уравнение кривой AB задано в параметрической форме
16

x = x(t), |
где x(t) |
и y(t) − |
непрерывные функции с |
t [α ; β ] , |
|||
y = y(t). |
|
|
|
непрерывными производными и x(α ) = a , x(β ) = b , то длина l кривой
AB находится по формуле
β |
|
|
|
|
|
|
|
|
|
l = ∫ |
|
′ |
2 |
|
′ |
2 |
dt . |
[5] |
|
|
(x (t)) |
|
+ ( y (t)) |
|
|||||
α |
|
|
|
|
|
|
|
|
|
Формула [5] может быть получена из формулы [4] подстановкой |
|||||||||
|
|
|
|
′ |
|
|
|
|
|
′ |
′ |
y (t) |
|
|
|
|
|
||
|
′ |
|
|
|
|
|
|||
x = x(t) , dx = x (t)dt , |
f (x) = |
|
|
|
|
|
|
||
|
|
|
x (t) |
|
|
|
|
|
|
Если кривая |
AB задана уравнением в |
полярных координатах |
r = r(ϕ) , α < ϕ < β . |
Предположим, что r(ϕ ) |
′ |
и r (ϕ) непрерывны на |
||
отрезке [α; β ] и если в равенствах x = r cosϕ , |
y = r sinϕ , связывающих |
|
полярные и декартовы координаты, параметром считать угол ϕ , то
кривую AB можно задать параметрически
|
|
|
x′ = r′(ϕ)cosϕ − r(ϕ)sinϕ, |
|
|
|
|||||||
Тогда |
|
ϕ′ |
′ |
|
|
|
|
. |
|
|
|||
|
|
|
yϕ = r (ϕ)sinϕ + r(ϕ)cosϕ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
2 |
+ |
′ |
2 |
|
= ...... |
′ |
2 |
+ (r(ϕ) |
2 |
. |
|
|
(xϕ ) |
|
( yϕ ) |
|
|
(r (ϕ)) |
|
|
|||||
x = r(ϕ)cosϕ,
= ϕ ϕ .
y r( )sin
β
Применяя формулу [5], получаем l = ∫ 
 r 2 + r′2 dϕ .
r 2 + r′2 dϕ .
α
17
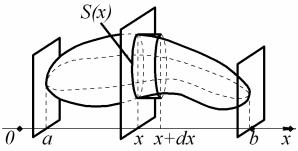
ВЫЧИСЛЕНИЕ ОБЪЁМА ТЕЛА
Вычисление объёма тела по известным площадям
параллельных сечений.
Пусть требуется найти объём V тела (рис. 9), причём известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ox : S = S (x) , a < x < b .
Применив схему II (метод дифференциала), получим формулу объёма тела по площади параллельных сечений
b |
|
V = ∫ S (x)dx . |
[6] |
a |
|
Рис. 9
Объём тела вращения
Пусть вокруг оси Ox вращается криволинейная трапеция, ограниченная непрерывной линией y = f (x) > 0 , отрезком a ≤ x ≤ b и
прямыми x = a и x = b (рис. 10). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ox , проведённой через произвольную точку x оси Ox ( x [a;b] ), есть круг с радиусом y = f (x) . Следовательно
S = π y2 .
18

Рис. 10
Применяя формулу [6] объёма тела по площади параллельных сечений, получаем
|
b |
|
Vx |
= π ∫ y2dx . |
[7] |
|
a |
|
Если криволинейная трапеция ограничена графиком непрерывной |
||
функции x = ϕ( y) ³ 0 |
и прямыми x = 0 , |
y = c , y = d ( c < d ), то объём |
тела, образованного вращением этой трапеции вокруг оси Oy , по аналогии с формулой [7] , равен
|
|
b |
|
|
|
||
|
Vy = π ∫ x2dy . |
|
|
[8] |
|||
|
|
a |
|
|
|
||
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ ВРАЩЕНИЯ |
|||||||
Пусть кривая |
AB является графиком функции |
y = f (x) ³ 0 , где |
|||||
x Î[a;b] , |
а функция |
y = f (x) и её производная |
′ |
|
′ |
||
y |
= f (x) непрерывны |
||||||
на этом |
отрезке, |
тогда площадь S поверхности, образованной |
|||||
вращением кривой AB вокруг оси Ox (рис. 11): |
|
|
|
||||
|
|
b |
|
|
|
||
|
|
Sx = 2π ∫ y × |
1 + ( y¢)2 |
dx . |
|
|
[9] |
a
19
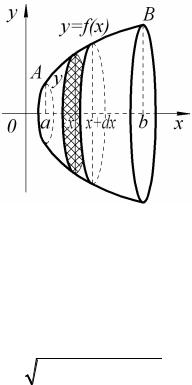
Рис. 11
Если кривая AB задана параметрическими уравнениями x = x(t), y = y(t) , где t1 ≤ t ≤ t2 , то формула [9] для площади поверхности вращения принимает вид
t2 |
|
|
|
Sx = 2π ∫ y(t) × (x¢(t))2 + ( y¢(t))2 dx . |
[10] |
||
t1 |
|
||
МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
Работа переменной силы
Пусть материальная точка M перемещается вдоль оси Ox под действием переменной силы F = F (x) , направленной параллельно этой
оси. Работа, произведённая силой |
при перемещении точки M из |
положения x = a в положение x = b ( a < b ), находится по формуле |
|
b |
|
A = ∫ F (x)dx |
[11] |
a |
|
Путь, пройденный телом |
|
Пусть материальная точка перемещается по прямой с переменной |
|
скоростью v = v(t) , тогда путь S , |
пройденный ею за промежуток |
времени от t1 до t2 : |
|
20
