
C22013
.pdf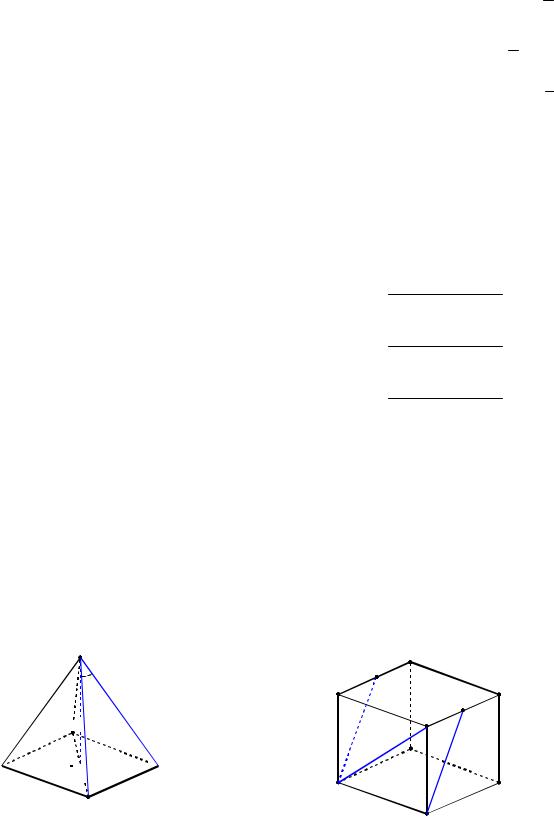
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Метод опорных задач
При решении задач этого типа можно воспользоваться опорными задачами № 2, 3 и 5 (глава 3 п. 3.4).
Применение теоремы «о трех косинусах»
Пусть величина угла между наклонной l и ее проекцией на некоторую плоскость, величина угла между проекцией наклонной l и прямой, проведенной через основание той же наклонной в плоскости проекции, и величина угла между наклонной l и прямой, проведенной через ее основание в плоскости проекции. Тогда справедливо следующее соотношение:
cos cos cos .
Доказательство теоремы приведено в главе 3 п. 3.4, опорная задача №3.
Пример 41. Угол между боковыми рёбрами правильной четырехугольной пирамиды, не лежащими в одной грани, равен 120 . Найти плоский угол при вершине пирамиды.
Решение. В правильной четырехугольной пирамиде SABCD проведем диагональное сечение ASC (см. рис. 47); SD – наклонная к плоскости сечения, SO
– высота пирамиды и проекция SD на эту плоскость, SC – прямая, проведенная в плоскости ASC через основание наклонной. По условию ASC 120 .
S
B

A











 O
O













 C
C
D
Рис. 47
Из теоремы о трех косинусах получаем:
cos DSC cos DSO cos CSO.
Отсюда
04.12.2012 |
31 |
cos DSC cos60 cos60 cos2 60 1 . 4
Следовательно, DSC arccos1 . 4
Ответ: arccos1 . 4
Применение теоремы косинусов для трехгранного угла
Во всяком трехгранном угле, плоские углы которого равны , и , а двугранные углы, противолежащие им, соответственно равны A , B и C , име-
ют место следующие равенства:
cos C cos cos cos , sin sin
cos B cos cos cos , sin sin
cos A cos cos cos .
Доказательство теоремы приведено в главе 3 п. 3.4, опорная задача №2.
Пример 42. В кубе ABCDA1B1C1D1
найти угол между прямыми AD1 и DM,
где М – середина ребра D1C1 .
Решение. Пусть ребро куба равно 1, точка N – середина ребра А1В1 , тогда искомый угол равен углу между AD1 и AN (см. рис. 48).
|
B1 |
|
A1 |
N |
|
C1 |
||
|
M |
|
|
D1 |
|
A |
B |
|
C |
||
|
D
Рис. 48
Используем теорему косинусов для трехгранного угла с вершиной A (опорная задача № 2), в котором A1 AD1 ,
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
A1AN , NAD1 . Так как в кубе все двугранные углы при ребрах прямые, то 90 . Тогда из теоремы следует, что
cos cos cos .
Из прямоугольного треугольника
A AD находим cos cos45 |
2 |
, из |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
треугольника A1AN получаем |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
AA1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
. |
|
|
||||||
|
cos |
|
|
1: |
|
|
|
5 |
|
|
|||||||||||||||||||
|
AN |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
5 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
. |
|
|
|
|
|||||||||
|
Отсюда cos |
|
|
|
2 |
|
2 |
|
|
|
|
|
|||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Следовательно, arccos |
|
2 |
. |
|
|
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
5
Ответ: arccos 2 . 5
Применение формулы
cos2 cos2 cos2 1,
где , и – углы, которые образует некоторая прямая с тремя попарно перпендикулярными прямыми.
Доказательство этой формулы приведено в главе 3 п. 3.4, опорная задача №5.
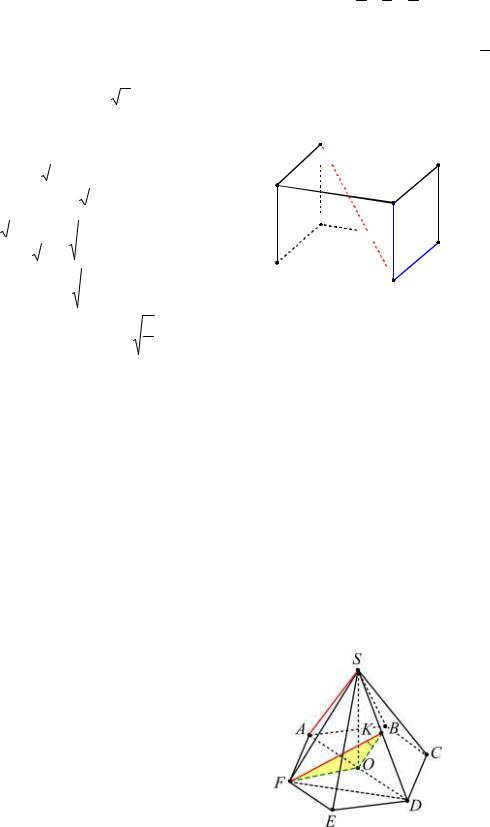
Пример 43. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Его диаго-
наль В1D составляет с ребром AD угол 45 , а с ребром DC угол 60 . Найти угол между прямыми В1D и DD1 .
Решение. Так как параллелепипед ABCDA1B1C1D1 прямоугольный, то его ребра, выходящие из одной вершины попарно перпендикулярны. Рассмотрим вершину D и воспользуемся данной выше формулой
cos2 cos2 cos2 1,
где ADB1 , CDB1 , D1DB1
(см. рис. 49).
Так как по условию 45 , 60 , то получаем
04.12.2012 |
32 |
cos2 45 cos2 60 cos2 1,
cos2 1 1 1 1 . 4 2 4
Поскольку – острый угол, то cos 1 . 2
Отсюда 60 .
Ответ: 60 .
B1


 C1
C1
A1
D1
B








 C
C
A
D
Рис. 49
Решение одной задачи разными методами
Пример 44. В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые рёбра равны 2, точка K – середина ребра SD. Найти косинус угла между прямыми AS и FK .
Решение. 1-й способ (поэтапновычислительный). Ребро AS и точка K
лежат в плоскости ASD, тогда средняя линия KO треугольника ASD будет па-
раллельна |
AS |
и |
угол |
(AS, FK) (KO, FK) |
(см. рис. 50). |
||
Точка O – центр основания пирамиды.
Рис. 50
Найдем угол FKO треугольника FKO. Для этого найдем длины его сторон. Так как в основании пирамиды ле-
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
жит правильный шестиугольник, то отрезок FO равен его стороне, то есть FO 1. Соответственно отрезок KO – средняя линия треугольника ASD и
KO AS 1. 2
Найдем FK . Рассмотрим равнобедренный треугольник FSD, в котором
FS SD 2, а FD 
 3 (меньшая диагональ правильного шестиугольника со стороной 1). Учитывая, что FK – медиана треугольника FSD получаем
3 (меньшая диагональ правильного шестиугольника со стороной 1). Учитывая, что FK – медиана треугольника FSD получаем
FK 1 
 2FS2 2FD2 SD2
2FS2 2FD2 SD2 
 10 . 2 2
10 . 2 2
Теперь из теоремы косинусов для треугольника FKO находим:
cos( FKO) FK2 KO2 FO2 
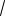 10 .
10 .
2 FK KO |
4 |
Учитывая, что
cos( (AS, FK)) |cos( FKO)|,
получаем, что искомый угол равен
arccos 
 10 . 4
10 . 4
Ответ: arccos 10 . 4
2-й способ (координатно-
векторный). Введем прямоугольную системукоординат, как указано на рисунке 51.
Так как пирамида правильная, то точка
O – центр |
основания |
пирамиды и из |
|||
прямоугольного треугольника ASO по- |
|||||
|
|
|
|
|
|
лучаем SO |
|
AS2 AO2 |
|
|
. |
|
3 |
||||
Рис. 51
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
А( 1;0;0), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(1;0;0), |
|||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
F |
|
|
; |
|
|
|
|
|
|
|
;0 |
, |
|
S(0;0; |
3). |
|
|
|
Учитывая, |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
что точка K – середина отрезка SD, по- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
лучаем |
K |
|
|
;0; |
|
|
|
|
|
|
|
|
|
. |
Отсюда |
имеем: |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
AS {1;0; |
|
|
|
|
|
|
|
|
|
FK |
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
3}, |
1; |
|
; |
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Используя формулу (5), находим: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
cos( (AS, FK)) |cos( (AS, FK))| |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
1 1 0 |
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
||||||||||||||||||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
1 0 |
|
|
( 3) |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда искомый угол равен arccos 10 . 4
Ответ: arccos 10 . 4
Тренировочные упражнения
51. В кубе ABCDA1B1C1D1 точка Е –
середина ребра A1В1 . Найдите косинус угла между прямыми AE и ВD1 .
52. В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и DM, где
М– середина ребра D1C1 .
53.(ЕГЭ, 2012). Точка E середина ребра DD1 куба ABCDA1B1C1D1 . Найдите
угол между прямыми CE и AC1.
54. (ЕГЭ, 2012). На ребре CC1 куба
ABCDA1B1C1D1 отмечена точка E так,
что CE :EC1 1:2. Найдите угол между прямыми BE и AC1.
55. В кубе ABCDA1B1C1D1 точки E ,
F середины ребер соответственно A1В1
и B1C1. Найдите косинус угла между прямыми AE и BF .
04.12.2012 |
33 |
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
56. В кубе ABCDA1B1C1D1 точки Е, F – середины рёбер соответственно A1В1 и
C1D1 . Найдите косинус угла между прямыми AE и BF.
57. В кубе ABCDA1B1C1D1 к диагонали
A1C провели перпендикуляры из вершин A и В. Найдите угол между этими перпендикулярами.
58.К диагонали куба провели перпендикуляры из остальных вершин куба. На сколько частей и в каком отношении основания этих перпендикуляров разделили диагональ?
59.В кубе ABCDA1B1C1D1 к диагонали
A1C провели перпендикуляры из середин ребер AB и AD. Найдите угол между этими перпендикулярами.
60. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Его диагональ В1D составляет с ребром AD угол 45 , а с ребром DC угол 60 . Найдите угол между прямыми В1D и DD1 .
61. Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда образуют с плоскостью его основания углы и . Найдите угол между этими диагоналями.
62. В правильной четырехугольной призме ABCDA1B1C1D1 сторона основания равна 12, а боковое ребро равно 5. Найдите угол между прямыми
AC и BC1.
63. В правильной треугольной призме ABCA1B1C1 , все рёбра которой равны 1, найдите косинус угла между прямыми:
а) AB и A1C ; б) AВ1 и BC1.
64. (МИОО). Сторона основания правильной треугольной призмы ABCA1B1C1 равна 8. Высота этой призмы равна 6. Найдите угол между прямыми CA1 и
AB1 .
65. В правильной треугольной призме ABCA1B1C1 , все рёбра которой равны 1,
точка D – середина ребра A1В1 . Найдите косинус угла между прямыми АD и BC1.
04.12.2012 |
34 |
66. В правильной треугольной призме ABCA1B1C1 , все рёбра которой равны 1, точки D, Е – середины рёбер соответственно A1В1 и B1C1. Найдите косинус угла между прямыми АD и ВЕ.
67. (МИОО). В основании прямой призмы ABCA1B1C1 лежит равнобедренный прямоугольный треугольник АВС с
гипотенузой AB , равной 8
 2 . Высота этой призмы равна 6. Найдите угол между прямыми AC1 и CB1.
2 . Высота этой призмы равна 6. Найдите угол между прямыми AC1 и CB1.
68. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найдите косинус угла между прямыми AB1 и BC1.
69. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найдите косинус угла между прямыми AB1 и BD1 .
70. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найдите угол между прямыми AB1 и BE1 .
71. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, точка G – середина ребра A1В1 . Найдите косинус угла между прямыми АG и BC1.
72. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, точка G – середина ребра A1В1 . Найдите косинус угла между прямыми AG и BD1 .
73. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, точки G, H – середины ребер соответственно A1В1 и B1C1. Найдите косинус угла между прямыми АG и BH.
74.Найдите угол между непересекающимися медианами граней правильного тетраэдра.
75.В правильном тетраэдре ABCD точка K – середина BD, точка M – середина BC. Найдите угол между прямыми
AK и DM.
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
76.В правильной четырёхугольной пирамиде SABCD (с вершиной S) боковое ребро равно стороне основания. Точка M
–середина ребра SB. Найдите угол между прямыми CM и SO, где точка O – центр основания пирамиды.
77.Ребра АD и ВС пирамиды DABC равны 24 см и 10 см. Расстояние между серединами ребер BD и AC равно 13 см. Найдите угол между прямыми АD и ВС.
78.В тетраэдре ABCD известно, что
AC BD 14, BC AD 13, AB
CD 15. Найдите угол между прямыми
АС и BD.
79.В правильной четырехугольной пирамиде SABCD, все рёбра которой равны 1, точки E , F – середины ребер соответственно SB и SC. Найдите косинус угла между прямыми АЕ и BF.
80.Угол между боковыми рёбрами правильной четырехугольной пирамиды, не лежащими в одной грани, равен 120 . Найдите плоский угол при вершине пирамиды.
81.В правильной шестиугольной пирамиде SABCDEF, стороны оснований которой равны 1, а боковые рёбра равны 2, найдите косинус угла между прямыми
SB и АЕ.
82.В правильной шестиугольной пирамиде SABCDEF, стороны оснований которой равны 1, а боковые рёбра равны 2, найдите косинус угла между прямыми
SB и АD.
83.В правильной шестиугольной пирамиде SABCDEF с основанием ABCDEF сторона основания равна 2, а боковое ребро равно 4. Точка M – середина SE.
Найдите |
угол |
между |
прямыми |
SB и CM. |
|
|
|
1.6.Угол между прямой и плоскостью
Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.
0 (a, ) 90 .
Угол между взаимно перпендикулярными прямой и плоскостью равен 90 .
Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается равным 0 .
Поэтапно-вычислительный метод
Угол между прямой l и плоскостью можно вычислить, если этот угол удается включить в прямоугольный треугольник в качестве одного из острых углов.
Пример 45. В правильной треугольной призме ABCA1B1C1 , все рёбра которой равны 1, найти угол между прямой АВ1 и
плоскостью АА1С1С .
Решение. Пусть D – середина А1С1,
тогда B1D – перпендикуляр к плоскости
АА1С1С , а D – проекция точки В1 на эту плоскость (см. рис. 52).
C1
B1

 D
D
A1

 C
C
B 
A
Рис. 52
Если – |
|
искомый угол, то sin |
B1D |
, |
||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB1 |
||
|
|
|
|
|
|
B D |
|
|
|
, |
|
|
|
|
||||
где AB |
|
, |
3 |
и поэтому |
||||||||||||||
2 |
||||||||||||||||||
|
|
|
||||||||||||||||
1 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin |
|
6 |
|
. Отсюда arcsin |
|
6 |
|
. |
|
|
||||||||
|
|
|
4 |
|
|
|
||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: arcsin 6 . 4
04.12.2012 |
35 |
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Пример 46. В правильной четырехугольной пирамиде MABCD , все рёбра которой равны 1, точка E середина ребра MC. Найти синус угла между прямой DE и плоскостью AMB .
Решение. Через вершину M проведем прямую параллельную прямой AD, и отложим на ней единичный отрезок MF
(см. рис. 53).
M F
E

 H
H
B












 C
C
A
 D
D
Рис. 53
Втетраэдре MDCF все ребра равны 1
иплоскость DFC параллельна плоскости AMB . Перпендикуляр EH, опущенный
из точки E на плоскость DFC, равен половине высоты тетраэдра MDFC , т.е.
равен |
6 |
(высота |
данного тетраэдра |
||||||||||||||||
6 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
равна |
|
6 |
|
|
– покажите самостоятельно). |
||||||||||||||
|
3 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
DE |
|
|
|
|
|||||
Угол между прямой |
и плоскостью |
||||||||||||||||||
AMB равен углу EDH, синус которого |
|||||||||||||||||||
равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EH |
|
|
|
|
: |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
6 |
3 |
2 |
|||||||||||
|
|
|
|
|
|
6 |
|
2 |
|
3 |
|
||||||||
|
|
|
|
|
DE |
|
|
|
|
|
|
||||||||
Ответ: 2 . 3
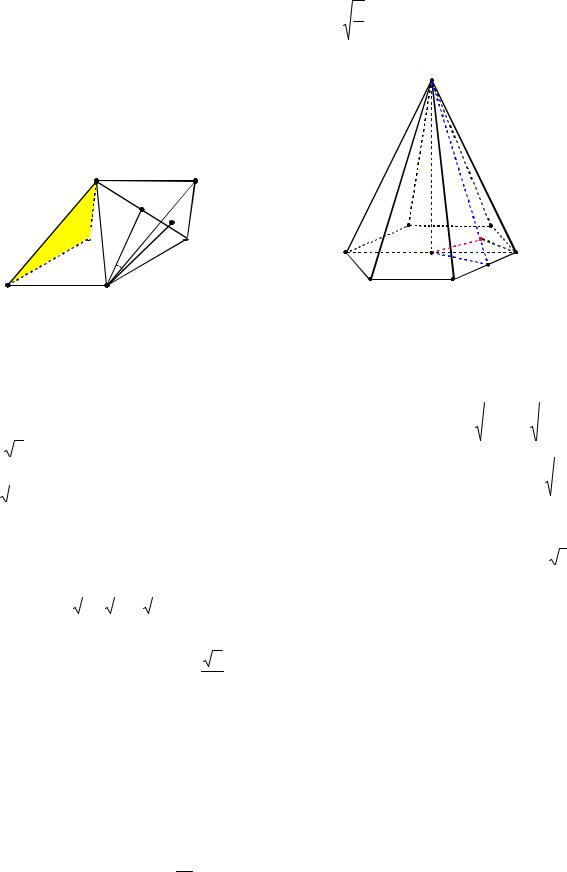
Пример 47. В правильной шестиугольной пирамиде MABCDEF, стороны основания которой равны 1, а боковые рёбра равны 4, найти синус угла между прямой BC и плоскостью EMD.
Решение. Так как AD|| BC, |
то |
(BC, EMD) (AD, EMD) (см. |
рис. |
54). Найдем sin (AD, EMD). |
|
Высота пирамиды MO 
 15 (см. пример 15). ML апофема боковой гра-
15 (см. пример 15). ML апофема боковой гра-
ни EMD. Высота OH треугольника MOL перпендикулярна плоскости EMD
и OH 5 . 7
M
|
B |
C |
|
|
|
|
|
|
|
|||||||
A |
|
|
H |
|
|
|
|
|
|
|
||||||
O |
|
|
|
|
D |
|
|
|
|
|
|
|
||||
|
|
|
L |
|
|
|
|
|
|
|
||||||
F |
|
E |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рис. 54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда прямая |
HD ортогональная про- |
|||||||||||||||
екция прямой |
AD на плоскость EMD и |
|||||||||||||||
из прямоугольного треугольника OHD |
||||||||||||||||
|
OH |
|
|
|
|
|
|
|
|
|
. |
|
|
|||
sin (AD, EMD) |
|
|
|
5 |
|
:1 |
5 |
|
||||||||
|
7 |
7 |
||||||||||||||
|
|
OD |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Ответ: |
|
|
5 |
. |
||||||||
|
|
|
|
7 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 48. (ЕГЭ, 2010). В правильной треугольной пирамиде MABC с основа-
нием ABC |
известны рёбра AB 7 3, |
MC 25. |
Найти угол, образованный |
плоскостью основания и прямой, проходящей через середины ребер AM и BC.
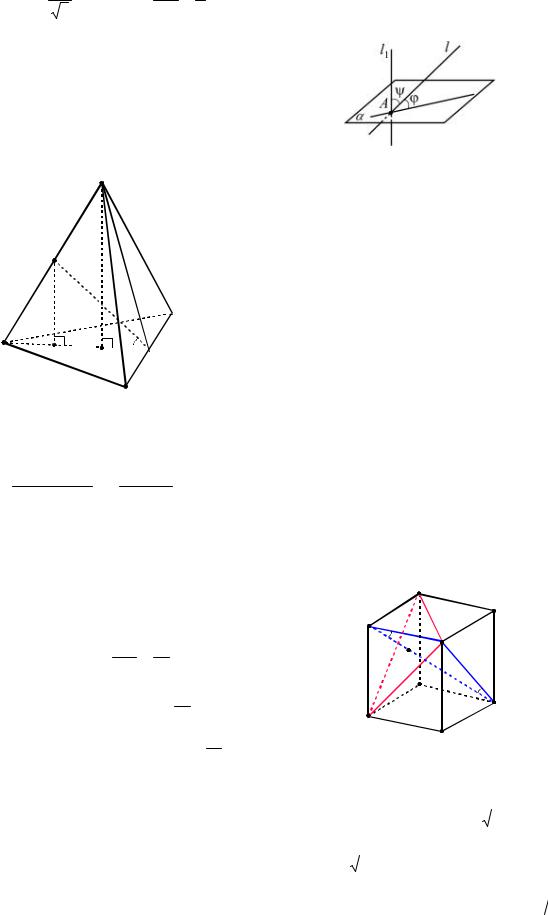
Решение. Пусть D и |
E середины |
рёбер CB и AM соответственно. Так как |
|
пирамида правильная, то |
AD CB и |
MD CB . Следовательно, |
CB ABC и |
ABC AMD (по признаку перпендикулярности плоскостей).
Опустим в плоскости AMD перпендикуляры MO и EF из точек M и E на прямую AD ABC AMD (см. рис. 55). Так как AD прямая пересечения перпендикулярных плоскостей, то MO и EF перпендикулярны к плоскости основания. Тогда точка O основание высоты MO является центром треугольника
04.12.2012 |
36 |
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
ABC и AO AB 7, OD AO 7 , а
|
FD |
3 |
2 |
2 |
прямая |
ортогональная |
проекция |
||
прямой |
DE |
на плоскость |
основания. |
|
Точка |
F |
середина отрезка |
AO |
|
(EF || MO и |
EF средняя линия |
тре- |
||
угольника AMO). Тогда |
|
|
||
|
FD FO OD 7. |
|
|
|
M
E
 B
B
A  F
F 
 O
O




 D
D
C
Рис. 55
Высоту пирамиды находим из прямоугольного треугольника AMO:
MO 
 AM2 AO2
AM2 AO2 
 252 72 24.
252 72 24.
Тогда EF 12
Так как угол между прямой и плоскостью – угол между прямой и ее ортогональной проекцией на эту плоскость, то из прямоугольного треугольника FED получаем
tg (ED, ABC) EF 12.
FD 7
Значит, искомый угол равен arctg12 . 7
Ответ: arctg12 . 7
Метод использования дополнительного угла
Угол между прямой l и плоскостьюи угол между прямой l и перпендикуляром к плоскости удовлетворяют соотношению 90 (см. рис. 56). Поэтому в некоторых случаях через до-
полнительный угол легко выйти на искомый угол .
Рис. 56
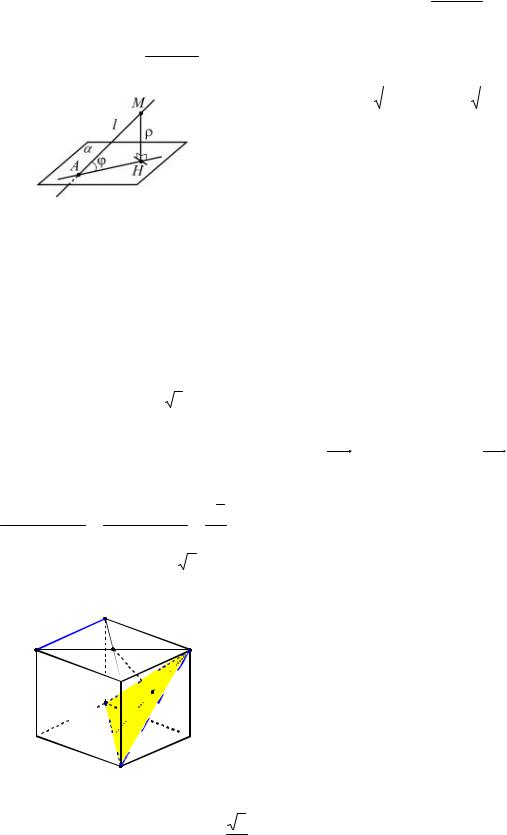
Пример 49. В единичном кубе ABCDA1B1C1D1 найти угол между пря-
мой CD1 и плоскостью AB1D1.
Решение. |
Прямая |
A1C1 B1D1 |
|
( A1B1C1D1 квадрат), тогда по теореме о |
|||
трех |
перпендикулярах |
A1C B1D1 (см. |
|
рис. |
57). Аналогично A1C AD1 . Следо- |
||
вательно, прямая A1C перпендикулярна плоскости AB1D1. Так как A1D1 D1C1C ,
то A1D1 D1C . Поэтому в прямоуголь-
ном треугольнике A1D1C |
D1CA1 |
|
|||||||||||||
есть угол между данной прямой CD1 и |
|||||||||||||||
перпендикуляром |
A1C к данной плоско- |
||||||||||||||
сти, а D1A1C , как дополнительный |
|||||||||||||||
угол до 90 для |
D1CA1 , является иско- |
||||||||||||||
мым углом. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
B1 |
C1 |
|
|
|
|
|||||
|
|
A1 |
|
|
|
|
|
|
|
||||||
|
|
|
D1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
E |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
B |
|
C |
|
|
|
|
||||
|
A |
|
|
|
|
|
|
|
|
||||||
|
|
D |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис. 57 |
|
|
|
|
|
|
|
|
||
Имеем |
|
|
|
cos |
A1D1 |
|
1 |
|
|
или |
|||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
A1C |
3 |
|
|
|
|
|
|||
arccos |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Ответ: arccos |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
 3
3
04.12.2012 |
37 |
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Метод опорных задач
Пусть прямая l пересекает плоскостьв точке A, точка M принадлежит прямой l (см. рис. 58). Тогда угол между прямой l и плоскостью можно вычислить, используя формулу:
sin sin (l, ) M, .
AM
Рис. 58
Пример 50. В единичном кубе ABCDA1B1C1D1 найти угол между пря-
мой А1B1 и плоскостью BDC1 .
Решение. Так как А1B1 ||D1C1 (см. рис.
59), то (A1B1, BDC1) (D1C1, BDC1).
Точки D1 и O1 лежат на прямой D1B1 ,
параллельной плоскости BDC1 , значит,
(D ;BDC ) (O ;BDC ) |
3 |
(см. |
|||
|
|||||
1 |
1 |
1 |
1 |
3 |
|
|
|
|
|
|
|
пример 14). Далее последовательно получаем
sin (A1B1, BDC1) sin (D1C1, BDC1)
(D1, BDC1) (O1, BDC1) 
 3 .
3 .
D1C1 D1C1 3
Отсюда (AB , BDC ) arcsin |
3 |
. |
|||
|
|||||
1 |
1 |
1 |
|
3 |
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
A1 |
|
|
O1 |
C1 |
|
|
|
|
|
||


 D1
D1 N
N






 B
B


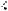


A











 O
O















 C
C
D
Рис. 59
Ответ: arcsin 3 . 3
04.12.2012 |
38 |
Векторно-координатный метод
Угол между прямой l и плоскостью можно вычислить по формуле
|
|
sin |
|
n |
p |
|
|
|
|
|
|
(6) |
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
n |
|
|
|
p |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
или в координатной форме |
|
|
|
|
|
|
|||||||||||||
sin |
|
|
|
x1x2 y1y2 |
z1z2 |
|
|
|
|
, |
|||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 |
y2 |
z2 |
x2 |
y2 |
z2 |
||||||||||||
1 |
1 |
|
|
|
1 |
|
|
|
|
2 |
2 |
2 |
|
|
|||||
где n {x1, y1, z1} – вектор нормали плос-
кости , p {x2, y2, z2} – направляющий вектор прямой l;
прямая l и плоскость параллельны тогда и только тогда, когда
x1x2 y1 y2 z1z2 0.
В задачах на вычисление угла между прямой и плоскостью или угла между пересекающимися плоскостями (будет рассмотрено позже) в общем случае уравнение плоскости находить не требуется.
Координаты вектора нормали можно вывести, если известны координаты трех точек плоскости M, N, P, не лежащих на одной прямой. Для этого находим коор-
динаты двух векторов плоскости
a MN {a1, a2, a3} и b MP {b1, b2, b3}.
Предположим, что вектор с координатами n {p, q, r} (здесь p, q, r – неизвестные числа, которые нужно найти) перпендикулярен любому вектору плос-
кости , в том числе векторам a и b . Его координаты ищутся из условий равенства нулю скалярных произведений n
с векторами a и b из следующей системы уравнений:
n a 0, |
a p a q a r 0, |
||
|
1 |
2 |
3 |
|
|
|
|
n b 0; |
b1 p b2q b3r 0. |
||
|
|
|
|
Эта система имеет бесконечное множество решений, так как векторов, перпендикулярных плоскости , бесконечно много. Выразив, например, из системы координаты p и q через r, выберем не-
нулевой вектор n {p(r); q(r); r}, взяв в качестве r какое-нибудь число (обычно
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
берут такое число, чтобы в координатах не было дробей или радикалов).
Пример 51. В единичном кубе ABCDA1B1C1D1 найти угол между пря-
мой АD1 и плоскостью , проходящей через точки А1 , Е и F, где точка Е – се-
редина ребра C1D1 , а точка F лежит на ребре DD1 , так, что D1F 2DF .
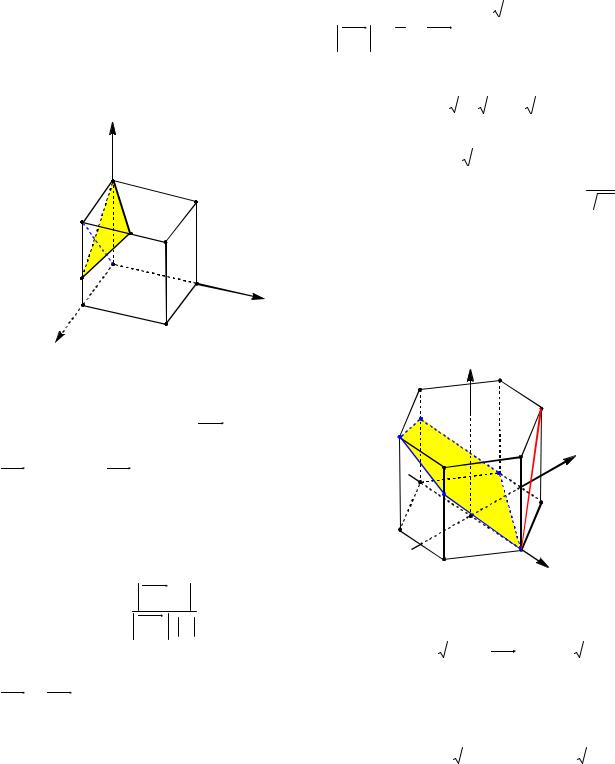
Решение. Введем прямоугольную системукоординат, как указано на рисунке60.
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
B1 |
|
|
|
D1 |
|
|
|
|
|
|
||
|
|
|
|
E |
|
|
|
||||
|
|
|
|
|
|
C1 |
|
|
|||
|
|
|
|
|
|
A |
|
|
|
B |
|
|
|
|
F |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
D |
|
|
|
|
|
|
y |
|
|
|
x |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Рис. 60 |
|
|
|||
Тогда |
А(0;0;0), |
А1(0;0;1), D1(1;0;1), |
|||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
Е 1; |
|
;1 |
, |
|
|
F 1;0; |
|
|
, |
АD1 {1;0;1}, |
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
||
A1E |
1; |
|
;0 |
, А1F 1;0; |
|
. |
|||||
2 |
|
||||||||||
|
|
|
|
|
|
|
|
3 |
|||
Пусть n {x, y, z} – вектор, перпендикулярный плоскости , – искомый угол. Тогда по формуле (6):
AD1 n sin AD1 n .
Вектор n найдем из условий перпендикулярности этого вектора векторам
A1E и А1F , т.е. из условий

n A1E 0,
n AF 01
или
04.12.2012
|
y |
|
|
|
|
|
|
||
x |
|
|
0, |
y 2x, |
|
||||
2 |
|
||||||||
|
|
|
|
||||||
|
2 |
|
|
|
|
||||
|
|
|
|
z 1,5x. |
|
||||
x |
|
|
|
z 0 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Пусть x 2, |
тогда |
|
y 4, |
z 3 и |
|||||
n {2; 4;3}, |
|
| n| |
|
|
. Так как |
||||
|
|
29 |
|||||||
AD1 
 2 и AD1 n 1 2 0 ( 4) 1 3 5,
2 и AD1 n 1 2 0 ( 4) 1 3 5,
то |
5 |
|
|
|
|
|
|
5 |
|
|
||||
sin |
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 29 |
58 |
|
|
|||||||||
Отсюда arcsin |
|
|
5 |
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
58 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: arcsin 5 .  58
58
Пример 52. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найти угол между прямой AB1 и плоскостью ACE1.
Решение. Введем прямоугольную системукоординат, как указано на рисунке61.
|
D1 |
|
|
|
|
|
|
|
|
z |
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
D |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
||||||||||||
E |
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Рис. 61 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||
А1;0;0 , B |
|
1 |
; |
|
|
;1 |
, |
AB |
|
|
|
1 |
; |
|
|
;1 . |
||||||||||||||||
|
1 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Составим уравнение плоскости, про- |
||||||||||||||||||||||||||||||||
ходящей через точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1;0;0 , |
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
1 |
|
|
3 |
|||||||||||||||
C |
|
; |
|
;0 |
|
, E |
|
|
; |
|
;1 . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
1 |
|
|
2 |
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Подставляя координаты этих точек в общее уравнение плоскости
39
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
ax by cz d 0,
получаем систему
|
|
a d 0, |
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
a |
3 |
|
b d 0, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
2 |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||
|
|
a |
|
|
|
|
|
b c d 0 |
|||
2 |
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
||||
Отсюда имеем |
|
|
|
|
a d , |
b |
|
d , |
|||
|
|
|
|
3 |
|||||||
c 3d . Подставим в уравнение плоскости и сократим на d 0:
x 
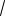 3y 3z 1 0.
3y 3z 1 0.
Вектор нормали полученной плоскости n {1; 
 3;3}. Тогда по формуле (6)
3;3}. Тогда по формуле (6)
AB1 n sin AB1 n ,
где искомый угол. Имеем
sin |
|
4 |
|
|
|
2 26 |
. |
|
|
|
|
|
|
|
|||
|
|
2 13 |
13 |
|
||||
Отсюда arcsin 2
 26 . 13
26 . 13
Ответ: arcsin 2 26 . 13
Векторный метод
Пример 53. В правильной четырехугольной пирамиде SABCD , все рёбра которой равны 1, найти угол между прямой DE, где E – середина апофемы SF грани ASB, и плоскостью ASC.
Решение. Так как прямая ОD перпенди-
кулярна плоскости ASC, то вектор OD является вектором нормали плоскости ASC.
Пусть |
AD a , |
AB b , |
AS c (см. |
||||||
рис. 62), |
где |
| a | |b | |c | 1, a b 0, |
|||||||
a c b c |a |2 cos60 0,5. Тогда |
|||||||||
|
|
|
OD OA AD |
|
|||||
|
|
1 |
|
|
|
1 |
|
|
|
|
|
(a b) a |
(a |
b), |
|||||
|
|
||||||||
|
2 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
DE DA AF FE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
b |
|
|
|
c |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
c , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
DE OD |
a |
|
|
|
|
|
b |
|
|
|
|
c |
|
|
|
|
|
|
a |
|
|
|
|
|
b |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
4 |
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1 |
|
2 |
|
|
1 |
|
|
2 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
3 |
|
|
|||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
a c |
|
|
|
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||||||||||||||||||||||||||
2 |
8 |
|
|
4 |
|
4 |
2 |
8 |
|
8 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
DE |
|
|
|
|
|
a |
|
|
|
|
b |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
1 |
|
|
2 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|||||||||||||||||||||||||
a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
c |
|
|
2 |
|
|
|
a c 2 |
|
|
|
|
|
|
|
|
b |
c |
||||||||||||||||||||||||||||||||||
|
16 |
4 |
|
|
|
2 |
4 |
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
1 |
|
1 |
|
1 |
|
1 |
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
8 |
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
S
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
B |
|
|
|
|
F |
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
OD |
|
|
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Подставляя |
|
полученные |
|
значения в |
|||||||||||||||||||||||||||||||||||
формулу (6) sin |
|
|
|
DE OD |
|
|
|
|
, имеем |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
DE |
|
OD |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
sin |
3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
8 |
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|||||||||
Отсюда arcsin |
|
|
3 |
|
|
, |
|
где искомый |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
30 |
|
||||||||||||||||||||||||||||||||||||
угол. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: arcsin |
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
04.12.2012 |
40 |
www.alexlarin.net
