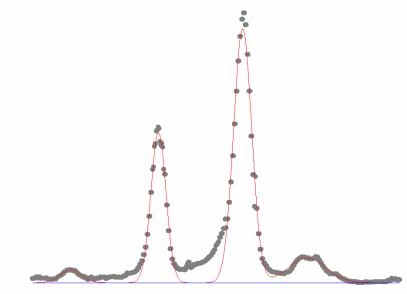
Определение степени кристалличности
Степень кристалличности – доля кристаллической фазы (%)
%cryst = Icryst/Icryst+Iam
Разделить интенсивность дифракции на вклады от кристаллической и аморфной части – сложная задача.
В настоящее время активно используется профильный анализ
Определение степени кристалличности полимеров
Последовательность действий:
1.Выбрать интервал углов 2θ, содержащий самые интенсивные рефлексы
2.Определить линию фона
3.Установить границы областей соответствующих кристаллической и аморфной фазам
4.Провести графическое (или какое-либо иное) интегрирование
5.Рассчитать %cryst.
Исследование наночастиц платины на углеродных нановолокнах методом рентгеновской дифракции как пример сравнения различных методов расчета размера кристаллитов
(областей когерентного рассеяния, размеров наночастиц)
С разрешения н.с. лаб. РСИ, к.х.н. ИНЭОС РАН И.С. Бушмаринова
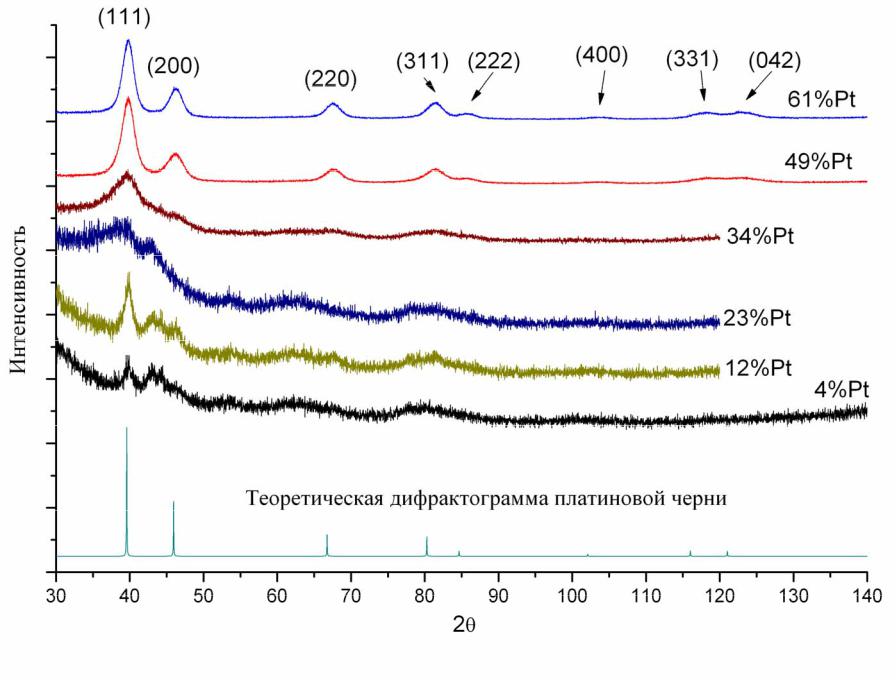
26. Дифрактограммы исследуемых образцов
Исследуемые образцы сильно отличаются содержанием платины
Чем меньше размер частиц – тем шире пики
27. Формула Шеррера – простейший способ определения
размера частиц
D = |
Kλ |
|
β cos( θ ) |
||
|
D – размер частицы
λ = 1,5406 Å
β –ширина пика на полувысоте, θ – угол дифракции (в радианах!),
K – константа, примерно равная 0,9
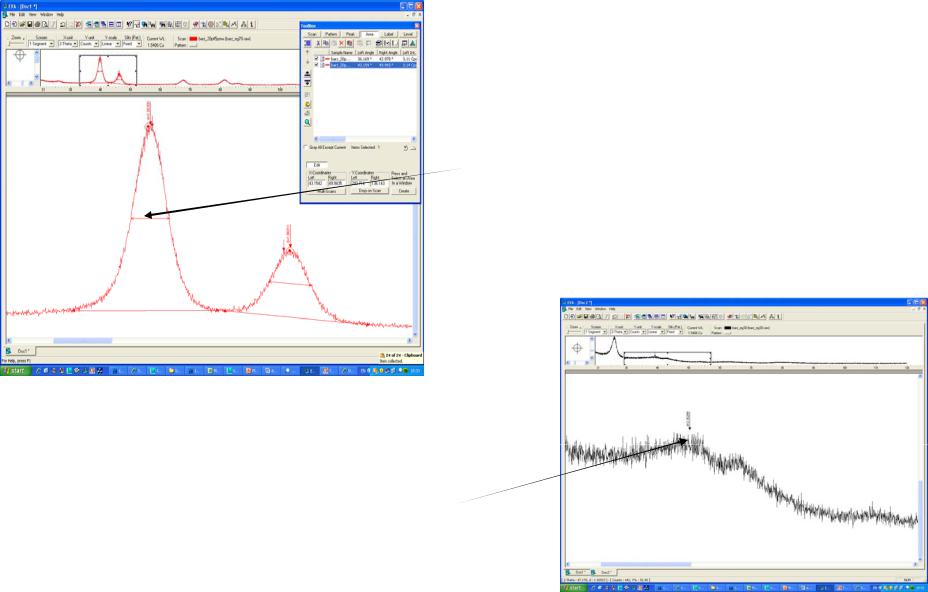
Соотнесение результатов с данными ПЭМ выявило сильные отличия.
В некоторых дифрактограммах было невозможно определить ширину пика
|
|
|
|
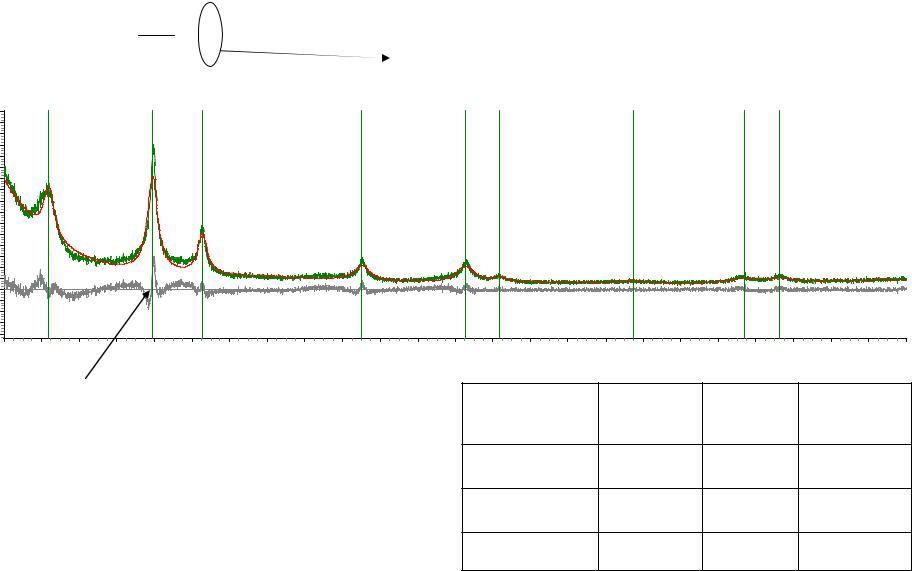
28. Метод Вильямсона-Холла (TOPAS) |
|
|
|
|
||||||||||||||||
β cos(θ) = kλ |
+ηsin(θ) |
|
|
|
параметр, отвечающий за отклонение |
|
|
|||||||||||||||||
|
|
|
|
D |
|
|
|
|
|
|
формы частиц от кубической |
|
|
|
|
|
||||||||
1,600 |
|
25.93239 |
|
39.74222 |
46.35538 |
|
|
|
67.55639 |
|
81.36622 |
|
|
103.7343 |
|
|
118.4194 |
|
|
|
|
|||
1,500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
85.83983 |
|
|
|
|
|
123.0875 |
|
|
|
||
1,400 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1,300 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
900 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
800 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
700 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
600 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-300 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-400 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
105 |
110 |
115 |
120 |
125 |
130 |
135 |
14 |
Форма линий описывается неправильно |
|
Масс. доля |
|
D(нм) D(нм) |
|
D(нм) |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pt (%) |
|
Шеррер |
TOPAS |
|
ПЭМ |
|
||||
|
|
|
|
Результаты сильно |
|
|
|
|
4 |
|
|
9.5 |
|
|
5.5 |
|
|
1.2 |
|
|||||
|
|
|
|
превышают данные ПЭМ |
|
|
12 |
|
|
9.9 |
|
|
3.9 |
|
|
1.6 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
3.7 |
|
|
1.1 |
|
|
2.1 |
|
R.L. Snyder, J. Fiala, H.J. Bunge, Defect and Microstructure Analysis by Diffraction, Oxford University Press, USA, 2000.