
- •Оглавление
- •Задачи с решениями
- •§2. Случайные события и их классификация. Алгебра событий. Вероятность события. Теоремы сложения и умножения вероятностей Случайные события
- •Вероятность события
- •Теоремы сложения и умножения вероятностей
- •Задачи с решениями
- •§3. Формула полной вероятности. Повторные испытания. Формула Бернулли Формула полной вероятности
- •Повторные испытания. Формула Бернулли
- •Формулы Лапласа
- •Формула Пуассона
- •Задачи с решениями
- •Глава 2. Случайные величины §4. Дискретная случайная величина Понятие случайной величины. Закон распределения дискретной случайной величины
- •Фунция распределения
- •Свойства функции распределения
- •Числовые характеристики дискретной случайной величины
- •Свойства математического ожидания
- •Свойства дисперсии
- •Некоторые законы распределения дискретной случайной величины
- •§5. Непрерывная случайная величина Понятие непрерывной случайной величины. Функция распределения непрерывной случайной величины
- •Свойства функции распределения
- •Функция плотности распределения вероятностей
- •Свойства функции плотности распределения вероятностей
- •Числовые характеристики непрерывной случайной величины
- •§6. Некоторые законы распределения непрерывной случайной величины Равномерный закон распределения
- •Показательный (экспоненциальный) закон распределения
- •Нормальный закон распределения
- •"Правило трех сигм"
- •Глава 3. Элементы математической статистики §7. Статистическое распределение выборки Задачи математической статистики
- •Генеральная и выборочная совокупности
- •Статистическое распределение выборки. Полигон и гистограмма
- •Свойства функции (х)
- •Задачи с решениями
- •§8. Статистические оценки параметров Точечные статистические оценки параметров распределения
- •Интервальные оценки параметров нормального распределения
- •Задачи с решениями
- •§9. Проверка статистических гипотез Статистические гипотезы
- •Проверка гипотез
- •Сравнение двух дисперсий нормальных генеральных совокупностей
- •Сравнение нескольких дисперсий нормальных генеральных совокупностей
- •Сравнение двух средних нормальных генеральных совокупностей
- •Задачи с решениями
- •§10. Критерий согласия Пирсона Проверка гипотезы о нормальном распределении
- •Задачи с решениями
- •§11. Элементы теории корреляции
- •Коэффициент корреляции
- •Свойства коэффициента корреляции
- •Проверка значимости выборочного коэффициента корреляции
- •Линейная корреляция. Уравнение регрессии
- •Ранговая корреляция
- •Правило проверки наличия связи между качественными признаками
- •Приложение 1 Контрольные работы и контрольные вопросы по теории
- •Элементы теории вероятностей
- •Элементы математической статистики
- •3. Контрольные вопросы по теории
- •Приложение 2 Вероятностные таблицы
- •Значения функции
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения f Фишера – Снедекора
§3. Формула полной вероятности. Повторные испытания. Формула Бернулли Формула полной вероятности
Пусть
событие А
может наступить при условии наступления
одного из несовместных событий
 ,
, ,
…
,
… ,
которые образуют полную группу. Поскольку
заранее неизвестно, какое из этих событий
наступит, их называют гипотезами. Пусть
известны вероятности этих событий
(гипотез) и условные вероятности событияА
при условии наступления каждого из них.
Как найти вероятность события А?
Ответ на этот вопрос даёт следующая
теорема.
,
которые образуют полную группу. Поскольку
заранее неизвестно, какое из этих событий
наступит, их называют гипотезами. Пусть
известны вероятности этих событий
(гипотез) и условные вероятности событияА
при условии наступления каждого из них.
Как найти вероятность события А?
Ответ на этот вопрос даёт следующая
теорема.
Теорема
1 (формула полной вероятности).
Вероятность события А,
которое может наступить лишь при условии
наступления одного из попарно несовместных
событий
 ,
, ,
…
,
… ,
образующих полную группу, равна сумме
произведений вероятностей каждого из
этих событий на соответствующую условную
вероятность событияА:
,
образующих полную группу, равна сумме
произведений вероятностей каждого из
этих событий на соответствующую условную
вероятность событияА:

Замечание
1.
Следствием формулы полной вероятности
является формула Байеса (по имени
английского математика, который её
вывел; опубликована в 1764 г.). Она позволяет
переоценить вероятность гипотезы
 ,
принятую до опыта, по результатам уже
проведённого опыта, т.е. вычислить
условную вероятность гипотезы
,
принятую до опыта, по результатам уже
проведённого опыта, т.е. вычислить
условную вероятность гипотезы при условии наступления событияА.
при условии наступления событияА.
Теорема
2 (формула Байеса или теорема гипотез).
Пусть попарно несовместные события
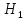 ,
, ,
…
,
… образуют
полную группу. Тогда условная вероятность
события
образуют
полную группу. Тогда условная вероятность
события (i
=
(i
=
 )
при условии, что событиеА
наступило,
задаётся формулой:
)
при условии, что событиеА
наступило,
задаётся формулой:
 (
( )
=
)
= =
= .
.
Повторные испытания. Формула Бернулли
Если производится несколько испытаний, причём вероятность наступления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Мы будем рассматривать такие независимые испытания, в которых события А имеют одну и ту же вероятность.
Теорема
3 (формула Бернулли).
Пусть в серии из n
одинаковых независимых испытаний в
каждом испытании может наступить либо
событие А
с вероятностью p,
либо событие
 с вероятностьюq
= 1
– p.
Тогда вероятность
с вероятностьюq
= 1
– p.
Тогда вероятность
 (m)
того, что в этой серии испытаний событие
А
наступит ровно m
раз (m
≤ n),
вычисляется по формуле Бернулли:
(m)
того, что в этой серии испытаний событие
А
наступит ровно m
раз (m
≤ n),
вычисляется по формуле Бернулли:
 (m)
=
(m)
=
 ∙
∙ ∙
∙ , где
, где =
=
Формулы Лапласа
Эти
формулы дают приближенное значение
вероятности наступления события А
определённое
число раз в серии из n
независимых испытаний, если число n
достаточно велико. Пусть p
(0
<p< 1)
–
вероятность события А
в каждом испытании, q
= 1
– p –
вероятность события
 .
.
Теорема
4 (локальная формула Лапласа).
Вероятность
 наступления события
А ровно
m
раз в серии из n
одинаковых
независимых испытаний приближённо
вычисляется по формуле Лапласа:
наступления события
А ровно
m
раз в серии из n
одинаковых
независимых испытаний приближённо
вычисляется по формуле Лапласа:
 (m)
(m)
 ∙
∙ ,
,
где
 ∙
∙ .
.
Замечание
2.
Имеются таблицы, в которых помещены
значения функции
 =
= ∙
∙ (в приложении 2 табл. П 2.1), соответствующие
положительным значениям аргументаx.
Для отрицательных значений аргумента
пользуются теми же таблицами, так как
функция φ(x)
является чётной, т.е. φ(x)
= φ(x).
(в приложении 2 табл. П 2.1), соответствующие
положительным значениям аргументаx.
Для отрицательных значений аргумента
пользуются теми же таблицами, так как
функция φ(x)
является чётной, т.е. φ(x)
= φ(x).
Замечание 3. Формула Лапласа тем точнее приближает формулу Бернулли, чем больше число n (более нескольких десятков) и n∙p > 10.
Теорема
5 (интегральная формула Лапласа).
Вероятность
 того, что событиеА
наступит от
того, что событиеА
наступит от
 до
до раз в серии изn
одинаковых независимых испытаний
приближённо вычисляется по формуле
Лапласа:
раз в серии изn
одинаковых независимых испытаний
приближённо вычисляется по формуле
Лапласа:
 (
( ,
, )
) Ф
(
Ф
( )
–Ф(
)
–Ф( ),
),
где
Ф(х)
=
 ∙
∙

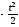 dt.
dt.
Замечание 4. Имеются таблицы, в которых помещены значения функции Ф(х) при 0 ≤ х ≤ 5 ( в приложении 2 табл. П 2.2). При х < 0 пользуются теми же таблицами, так как функция Ф(х) является нечётной, т.е. Ф( х) = = Ф(х). Для х > 5 можно считать Ф(х) = 0,5.
