
- •Оглавление
- •Задачи с решениями
- •§2. Случайные события и их классификация. Алгебра событий. Вероятность события. Теоремы сложения и умножения вероятностей Случайные события
- •Вероятность события
- •Теоремы сложения и умножения вероятностей
- •Задачи с решениями
- •§3. Формула полной вероятности. Повторные испытания. Формула Бернулли Формула полной вероятности
- •Повторные испытания. Формула Бернулли
- •Формулы Лапласа
- •Формула Пуассона
- •Задачи с решениями
- •Глава 2. Случайные величины §4. Дискретная случайная величина Понятие случайной величины. Закон распределения дискретной случайной величины
- •Фунция распределения
- •Свойства функции распределения
- •Числовые характеристики дискретной случайной величины
- •Свойства математического ожидания
- •Свойства дисперсии
- •Некоторые законы распределения дискретной случайной величины
- •§5. Непрерывная случайная величина Понятие непрерывной случайной величины. Функция распределения непрерывной случайной величины
- •Свойства функции распределения
- •Функция плотности распределения вероятностей
- •Свойства функции плотности распределения вероятностей
- •Числовые характеристики непрерывной случайной величины
- •§6. Некоторые законы распределения непрерывной случайной величины Равномерный закон распределения
- •Показательный (экспоненциальный) закон распределения
- •Нормальный закон распределения
- •"Правило трех сигм"
- •Глава 3. Элементы математической статистики §7. Статистическое распределение выборки Задачи математической статистики
- •Генеральная и выборочная совокупности
- •Статистическое распределение выборки. Полигон и гистограмма
- •Свойства функции (х)
- •Задачи с решениями
- •§8. Статистические оценки параметров Точечные статистические оценки параметров распределения
- •Интервальные оценки параметров нормального распределения
- •Задачи с решениями
- •§9. Проверка статистических гипотез Статистические гипотезы
- •Проверка гипотез
- •Сравнение двух дисперсий нормальных генеральных совокупностей
- •Сравнение нескольких дисперсий нормальных генеральных совокупностей
- •Сравнение двух средних нормальных генеральных совокупностей
- •Задачи с решениями
- •§10. Критерий согласия Пирсона Проверка гипотезы о нормальном распределении
- •Задачи с решениями
- •§11. Элементы теории корреляции
- •Коэффициент корреляции
- •Свойства коэффициента корреляции
- •Проверка значимости выборочного коэффициента корреляции
- •Линейная корреляция. Уравнение регрессии
- •Ранговая корреляция
- •Правило проверки наличия связи между качественными признаками
- •Приложение 1 Контрольные работы и контрольные вопросы по теории
- •Элементы теории вероятностей
- •Элементы математической статистики
- •3. Контрольные вопросы по теории
- •Приложение 2 Вероятностные таблицы
- •Значения функции
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения f Фишера – Снедекора
§2. Случайные события и их классификация. Алгебра событий. Вероятность события. Теоремы сложения и умножения вероятностей Случайные события
Определение 1. Испытанием (или опытом) называется осуществление некоторой совокупности определённых условий.
Определение 2. Событием называется любой результат испытания.
Определение 3. Событие называется случайным (обозначается прописными латинскими буквами: А, В, С, …, А1, А2, А3…), если в данном испытании оно может или произойти, или не произойти.
Определение 4. Событие называется достоверным (обозначается Е), если в данном испытании оно обязательно произойдёт.
Определение
5. Событие
называется невозможным
(обозначается ),
если в данном испытании оно никогда не
произойдёт.
),
если в данном испытании оно никогда не
произойдёт.
Определение 6. События называются несовместными в данном испытании, если они не могут наступить одновременно. В противном случае события называются совместными.
Определение 7. Событие В называется независимым от события А, если наступление события А не влияет на наступление или ненаступление события В. В противном случае события А и В называются зависимыми.
Определение 8. События называются равновозможными, если есть основание считать, что ни одно из них не является более возможным, чем остальные.
Определение 9. Говорят, что события А1, А2, … , Аn образуют полную группу событий, если в результате испытания обязательно наступает хотя бы одно из них.
Определение 10. Говорят, что события А1, А2, … , Аn образуют полную группу равновозможных попарно несовместных событий, если в данном испытании события А1, А2, … , Аn являются равновозможными и любые два из них – несовместные. Такие события будут называться элементарными событиями (или случаями, исходами).
Определение
11. Элементарное
событие
 называется благоприятствующим событию
А
, если его наступление влечёт
за собой наступление события А.
называется благоприятствующим событию
А
, если его наступление влечёт
за собой наступление события А.
Определение 12. Событие, обозначаемое Ā, называется противоположным событием по отношению к событию А, если наступление одного из них в результате данного испытания исключает наступление другого.
Алгебра событий
Определение 13. Суммой (или объединением) событий А и В называется такое событие, обозначаемое А+В, которое состоит в наступлении хотя бы
одного из событий А или В.
Определение 14. Произведением (или совмещением) событий А и В называется такое событие, обозначаемое А∙В, которое состоит в одновременном наступлении и события А, и события В.
Замечание 1. Если события А1, А2, … , Аn образуют полную группу попарно несовместных событий, то справедливы равенства:
А1 +А2+ … +Аn = Е,
Аi
∙
Аj=
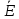 (i
≠ j).
(i
≠ j).
Замечание 2. Поскольку события А и Ā образуют полную группу и несовместны, для них справедливы равенства:
А + Ā = Е,
А
∙ Ā
=
 .
.
Вероятность события
Пусть для данного испытания события А1, А2, … , Аn образуют полную группу равновозможных попарно несовместных событий (являются элементарными событиями).
Определение 15. Вероятностью случайного события А в данном испытании называется число, обозначаемое Р(А) и вычисляемое по формуле:
Р(А)
=
 , (1)
, (1)
где n – число всех возможных элементарных событий рассматриваемого испытания; m – число благоприятствующих событию А.
Замечание 3. Ситуация, когда полную группу составляют равновозможные события, называется классической. Поэтому определение вероятности (1), опирающееся на такое условие, называется классическим определением вероятности.
Замечание 4. Нетрудно видеть, что в формуле (1) числа m, n связаны неравенствами:
0 ≤ m ≤ n.
Поэтому вероятность любого события А удовлетворяет неравенству:
0 ≤ P(A) ≤ 1.
Причём,
если А
= Е
– достоверное событие, то m
= n
и Р(Е)
= 1; если А
=
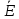 – невозможное событие, тоm
=
0 и
Р (
– невозможное событие, тоm
=
0 и
Р ( )=
0.
)=
0.
