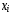- •Оглавление
- •Задачи с решениями
- •§2. Случайные события и их классификация. Алгебра событий. Вероятность события. Теоремы сложения и умножения вероятностей Случайные события
- •Вероятность события
- •Теоремы сложения и умножения вероятностей
- •Задачи с решениями
- •§3. Формула полной вероятности. Повторные испытания. Формула Бернулли Формула полной вероятности
- •Повторные испытания. Формула Бернулли
- •Формулы Лапласа
- •Формула Пуассона
- •Задачи с решениями
- •Глава 2. Случайные величины §4. Дискретная случайная величина Понятие случайной величины. Закон распределения дискретной случайной величины
- •Фунция распределения
- •Свойства функции распределения
- •Числовые характеристики дискретной случайной величины
- •Свойства математического ожидания
- •Свойства дисперсии
- •Некоторые законы распределения дискретной случайной величины
- •§5. Непрерывная случайная величина Понятие непрерывной случайной величины. Функция распределения непрерывной случайной величины
- •Свойства функции распределения
- •Функция плотности распределения вероятностей
- •Свойства функции плотности распределения вероятностей
- •Числовые характеристики непрерывной случайной величины
- •§6. Некоторые законы распределения непрерывной случайной величины Равномерный закон распределения
- •Показательный (экспоненциальный) закон распределения
- •Нормальный закон распределения
- •"Правило трех сигм"
- •Глава 3. Элементы математической статистики §7. Статистическое распределение выборки Задачи математической статистики
- •Генеральная и выборочная совокупности
- •Статистическое распределение выборки. Полигон и гистограмма
- •Свойства функции (х)
- •Задачи с решениями
- •§8. Статистические оценки параметров Точечные статистические оценки параметров распределения
- •Интервальные оценки параметров нормального распределения
- •Задачи с решениями
- •§9. Проверка статистических гипотез Статистические гипотезы
- •Проверка гипотез
- •Сравнение двух дисперсий нормальных генеральных совокупностей
- •Сравнение нескольких дисперсий нормальных генеральных совокупностей
- •Сравнение двух средних нормальных генеральных совокупностей
- •Задачи с решениями
- •§10. Критерий согласия Пирсона Проверка гипотезы о нормальном распределении
- •Задачи с решениями
- •§11. Элементы теории корреляции
- •Коэффициент корреляции
- •Свойства коэффициента корреляции
- •Проверка значимости выборочного коэффициента корреляции
- •Линейная корреляция. Уравнение регрессии
- •Ранговая корреляция
- •Правило проверки наличия связи между качественными признаками
- •Приложение 1 Контрольные работы и контрольные вопросы по теории
- •Элементы теории вероятностей
- •Элементы математической статистики
- •3. Контрольные вопросы по теории
- •Приложение 2 Вероятностные таблицы
- •Значения функции
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения f Фишера – Снедекора
§10. Критерий согласия Пирсона Проверка гипотезы о нормальном распределении
Критерием согласия называется критерий проверки гипотезы о предполагаемом законе распределения.
Критерий согласия Пирсона (критерий проверки гипотезы о нормальном распределении генеральной совокупности):
По выборке объема n построить статистический ряд:
|
xi |
x1 |
x2 |
… |
xl |
|
mi |
m1 |
m2 |
… |
ml |
2)
Вычислить по таблице оценку математического
ожидания
 и выборочное среднее квадратическое
отклонение σв.
и выборочное среднее квадратическое
отклонение σв.
3) В предположении нормального распределения генеральной совокупности вычислить теоретические частоты m1 теор ,…, ml теор по формуле:
m1 теор=n · pi ,
где
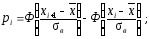 Ф(x)
– интегральная функция распределения
Лапласа
табл. П 2.2(см. приложение 2).
Ф(x)
– интегральная функция распределения
Лапласа
табл. П 2.2(см. приложение 2).
4) Вычислить число χ2набл по формуле:
χ2набл
=
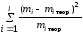 илиχ2набл
=
илиχ2набл
= .
.
5) По табл. П 2.5 (приложение 2) найти число χ2крит , учитывая заданный уровень значимости α и число степеней свободы k = l – 3 .
6) Сравнить числа χ2набл и χ2крит :
если χ2набл < χ2крит , то нет основания отвергать гипотезу о нормальном распределении генеральной совокупности.
если χ2набл > χ2крит , то гипотезу о нормальном распределении генеральной совокупности следует отвергнуть.
Замечание 1. Объем выборки n должен быть достаточно велик (больше 100). Число l обычно выбирают в диапазоне от 7 до 15. Поэтому при составлении интервального статистического ряда не используют интервалы, содержащие малое число значений объединяя их в один и суммируя соответствующее число значений.
Замечание 2. В случае χ2набл < χ2крит , для избежания ошибки первого рода следует повторить опыт, увеличив число n.
Замечание 3. При использовании критерия Пирсона с целью систематизации записи рекомендуется записывать все промежуточные вычисления в виде следующей таблицы:
|
№ |
xi |
mi |
mi2 |
mi теор |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
… |
|
|
|
|
|
|
l |
|
|
|
|
|
|
∑ |
|
n |
|
n |
χ2набл |
Задачи с решениями
Задача 10.1. Отделом технического контроля качества продукции произведен выбор 200 деталей для измерения отклонений их действительного диаметра от планируемого. Данные измерений приведены в табл. 10.1.
Таблица 10.1
|
[ai ; ai+1) |
mi |
|
[–20 ; –15) |
7 |
|
[–15 ; –10) |
11 |
|
[–10 ; –5) |
15 |
|
[–5 ; 0) |
24 |
|
[0 ; 5) |
49 |
|
[5 ; 10) |
41 |
|
[10 ; 15) |
26 |
|
[15 ; 20) |
17 |
|
[20 ; 25) |
7 |
|
[25 ; 30) |
3 |
Оценить с помощью критерия Пирсона гипотезу о нормальном распределении генеральной совокупности при уровне значимости α = 0,05 .
Решение.
Перейдем
от интервального статистического ряда
к статистическому ряду, заменив каждый
промежуток [ai
;
ai+1)
его средним значением
 . Получаем табл. 10.2.
. Получаем табл. 10.2.
По
табл. 10.2 вычислим математическое ожидание
 ,
дисперсиюDв
и среднее квадратическое отклонение
σв
:
,
дисперсиюDв
и среднее квадратическое отклонение
σв
:
Таблица 10.2
|
|
mi |
|
17,5 |
7 |
|
12,5 |
11 |
|
7,5 |
15 |
|
2,5 |
24 |
|
2,5 |
49 |
|
7,5 |
41 |
|
12,5 |
26 |
|
17,5 |
17 |
|
22,5 |
7 |
|
27,5 |
3 |
По
табл. 10.2 вычислим математическое ожидание
 ,
дисперсиюDв
и среднее квадратическое отклонение
σв
:
,
дисперсиюDв
и среднее квадратическое отклонение
σв
:
 =
=
=
+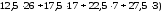 =
= ;
;
Dв =
=
=
+ =
=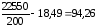 ;
;
σв.= =9,71.
=9,71.
Дальнейшие вычисления выполним по алгоритму критерия согласия Пирсона и оформим их в виде табл. 10.3, причем x1= – ∞, x9= +∞ .
Таблица 10.3
|
№ |
xi |
mi |
mi2 |
pi |
mi теор= =200 · pi |
|
|
1 |
17,5 |
7 |
49 |
0,0233 |
4,66 |
10,52 |
|
2 |
12,5 |
11 |
121 |
0,0475 |
9,5 |
12,74 |
|
3 |
7,5 |
15 |
225 |
0,0977 |
19,54 |
11,52 |
|
4 |
2,5 |
24 |
576 |
0,1615 |
32,3 |
17,83 |
|
5 |
2,5 |
49 |
2401 |
0,1979 |
39,58 |
60,66 |
|
6 |
7,5 |
41 |
1681 |
0,1945 |
38,9 |
43,22 |
|
7 |
12,5 |
26 |
676 |
0,1419 |
28,38 |
23,82 |
|
8 |
17,5 |
17 |
289 |
0,0831 |
16,62 |
17,39 |
|
9 |
27,5 |
10 |
100 |
0,0526 |
10,52 |
9,51 |
|
∑ |
|
200 |
|
|
200 |
207,21 |
Следовательно, находим χ2набл = 207,21 – 200 = 7,21.
Из табл. П 2.5 (приложение 2) с учетом значений α = 0,05 k = l – 3 = 6 находим: χ2набл =12,6.
Так как 7,21 < 12,6, т.е. χ2набл < χ2крит , то нет основания отвергать гипотезу о нормальном распределении генеральной совокупности.
Ответ: принимаем гипотезу о нормальном распределении генеральной совокупности.
Задача 10.2. В результате контрольных испытаний из генеральной совокупности взята выборка объема n=200 :
Таблица 10.4
|
xi |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
|
mi |
16 |
24 |
28 |
32 |
25 |
24 |
20 |
18 |
15 |
Оценить с помощью критерия Пирсона гипотезу о нормальном распределении генеральной совокупности при уровне значимости α = 0,01.
Решение.
1)
По табл. 10.4 вычислим выборочные
математическое ожидание
 ,
дисперсиюDв
и
среднее квадратическое отклонение σв:
,
дисперсиюDв
и
среднее квадратическое отклонение σв:
 =
=
=

 ;
;
Dв =
=
=
 ;
;
σв.= =4,51.
=4,51.
2) Дальнейшие вычисления выполним по алгоритму критерия согласия Пирсона и оформим их в виде табл. 10.5.
Таблица 10.5
|
№ |
xi |
mi |
mi2 |
pi |
mi теор = =200 · pi |
|
|
1 |
6 |
16 |
256 |
0,0446 |
8,92 |
28,70 |
|
2 |
8 |
24 |
576 |
0,0592 |
11,84 |
48,65 |
|
3 |
10 |
28 |
784 |
0,1023 |
20,46 |
38,32 |
|
4 |
12 |
32 |
1024 |
0,1496 |
29,92 |
34,23 |
|
5 |
14 |
25 |
625 |
0,1722 |
34,44 |
18,15 |
|
6 |
16 |
24 |
576 |
0,1671 |
33,42 |
17,24 |
|
7 |
18 |
20 |
400 |
0,1339 |
26,78 |
14,94 |
|
8 |
20 |
18 |
324 |
0,0903 |
18,06 |
17,94 |
|
9 |
22 |
15 |
225 |
0,0808 |
16,16 |
13,92 |
|
∑ |
|
200 |
|
1 |
200 |
232,09 |
Следовательно, находим: χ2набл =232,09 – 200 = 32,09 .
Из табл. 10.5 (приложение 2) с учетом значений α = 0,01 k = l – 3 = 6 находим: χ2крит =16,8. Так как 32,09 >16,8 , то χ2набл > χ2крит . Следовательно, отвергаем гипотезу о нормальном распределении генеральной совокупности.
Ответ: отвергаем гипотезу о нормальном распределении генеральной совокупности.
Задача 10.3. Используя критерий Пирсона, при уровне значимости α=0,05 установить, случайно или значимо расхождение между эмпирическими частотами mi и теоретическими частотами mi теор ,которые вычислены, исходя их гипотезы о нормальном распределении генеральной совокупности:
|
mi |
6 |
10 |
36 |
56 |
32 |
20 |
12 |
8 |
|
mi теор |
4 |
9 |
25 |
60 |
35 |
24 |
14 |
9 |
Решение. 1) Найдем χ2набл:
χ2набл
=
 =
=

 =
=

Из табл. 10.5 (приложение 2) с учетом значений α = 0,05 k = 8– 3 = 5 находим: χ2крит =11,1.
Так как 7,54 < 11,1 то χ2набл < χ2крит . Следовательно, нет основания отвергать гипотезу о нормальном распределении генеральной совокупности.
Ответ: расхождение случайное.
Задачи
10.1. Используя критерий Пирсона, при уровне значимости α = 0,05 установить, случайно или значимо расхождение между эмпирическими частотами mi и теоретическими частотами mi теор ,которые вычислены, исходя из гипотезы о нормальном распределении генеральной совокупности:
а)
|
mi |
7 |
11 |
31 |
14 |
7 |
|
mi теор |
6 |
15 |
30 |
14 |
5 |
б)
|
mi |
10 |
17 |
23 |
31 |
29 |
20 |
12 |
8 |
|
mi теор |
7 |
12 |
21 |
45 |
28 |
19 |
11 |
7 |
в)
|
mi |
8 |
18 |
35 |
28 |
22 |
18 |
11 |
|
mi теор |
5 |
11 |
28 |
43 |
31 |
16 |
6 |
10.2. Используя критерий Пирсона, при уровне значимости α = 0,05 проверить гипотезу о нормальном распределении генеральной совокупности по ее выборке объема n = 200 :
|
№ |
xi |
mi |
|
1 |
1,2 |
6 |
|
2 |
1,4 |
9 |
|
3 |
1,6 |
26 |
|
4 |
1,8 |
25 |
|
5 |
2,0 |
30 |
|
6 |
2,2 |
26 |
|
7 |
2,4 |
21 |
|
8 |
2,6 |
24 |
|
9 |
2,8 |
20 |
|
10 |
3,0 |
8 |
|
11 |
3,2 |
5 |
10.3. Используя критерий Пирсона, при уровне значимости α = 0,05 проверить гипотезу о нормальном распределении генеральной совокупности по ее выборке объема n=150 , собранной в интервальный статистический ряд:
|
[ai ; ai+1) |
mi |
|
[0 ; 4) |
8 |
|
[4 ; 8) |
12 |
|
[8 ; 12) |
19 |
|
[12 ; 16) |
42 |
|
[16 ; 20) |
24 |
|
[20 ; 24) |
20 |
|
[24 ; 28) |
16 |
|
[28 ; 32] |
9 |
10.4. Используя критерий Пирсона, при уровне значимости α = 0,05 проверить гипотезу о нормальном распределении генеральной совокупности по ее выборке:

10.5. Используя критерий Пирсона, при уровне значимости α = 0,05 проверить гипотезу о нормальном распределении генеральной совокупности по ее выборке:

Ответы
10.1. а) Расхождение частот случайное (χ2набл = 2,07; χ2крит = 6);
б) Расхождение частот случайное (χ2набл = 8,23; χ2крит = 11,1);
в) Расхождение частот значимое (χ2набл = 20,26; χ2крит = 9,5).
10.2. Гипотеза о нормальном распределении принимается
(χ2набл = 7,71; χ2крит = 15,5).
10.3. Гипотеза о нормальном распределении принимается
(χ2набл = 8,065; χ2крит = 15,1).
10.4. Гипотеза о нормальном распределении отвергается
(χ2набл = 15,97; χ2крит = 7,8).
10.5. Гипотеза о нормальном распределении отвергается
(χ2набл = 15,46; χ2крит = 13,3).