§5. Непрерывная случайная величина Понятие непрерывной случайной величины. Функция распределения непрерывной случайной величины

Определение 1. Непрерывной называют величину, все возможные значения которой полностью заполняют конечный или бесконечный промежуток числовой оси.

Очевидно, число возможных значений непрерывной случайной величины бесконечно.

Непрерывную случайную величину можно задавать с помощью функции распределения.

Определение 2. Функцией распределения непрерывной случайной величины Х называется функция F(х), определяющая для каждого значения вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х:

F(x)=P(X<x), где хR.

Функцию распределения иногда называют интегральной функцией распределения.

Свойства функции распределения

1)0≤ F(x) ≤1.

2) У непрерывной случайной величины функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

3) Вероятность попадания случайной величины Х в один из промежутков (а;b), [а;b), (a;b], [а;b], равна разности значений функции F(х) в точках а и b, т.е. Р(а<Х<b)= F(b) F(a).

4) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение равна 0.

5) F(∞)=0, F(+∞)=1.

Задание непрерывной случайной величины с помощью функции распределения не является единственным.

Функция плотности распределения вероятностей

Определение 3. Функцией плотности распределения вероятностей f(x) (или плотностью распределения) непрерывной случайной величины Х называется производная от ее функции распределения, т.е.:

f(x)=(x)

Плотность распределения вероятностей иногда называют дифференциальной функцией распределения или дифференциальным законом распределения.

График функции плотности распределения вероятностей f(x) называется кривой распределения.

Свойства функции плотности распределения вероятностей

1. f(x) ≥0, при .

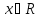2. F(x)= .

Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения, снизу осью Ох и лежащей левее точки х (рис. 5.1).

3. P (aXb)= .

Геометрически полученная вероятность равна площади криволинейной трапеции, ограниченной сверху кривой распределения, снизу осью Ох, слева и справа прямыми х = а, х = b (рис. 5.2).

4) – условие нормировки.

Рис. 5.1 Рис. 5.2

Задача 5.1. Случайная величина Х задана плотностью распределения вероятностей:

Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в) Р(3≤ х <5)

Решение:

а) Значение с найдем из условия нормировки:

Следовательно,

_{+∞ 2 6 +∞ 6 6}

∫ f(x)dx = ∫ 0dx + ∫ c(х  2)dx +∫ 0dx= c ∫(х  2)dx = с (х²/22х) =

^{∞ ∞ 2 6 2 2}

= c (36/2–12 – (4/2 – 4) = 8с;

с =1/8.

б) Известно, что F(x)=

Поэтому,

если х ≤ 2, то F(x)=;

если 2 < х ≤ 6, то F(x)=

х²х=х²/22х (4/24))1/8(х²/22х+2)=1/16(х2)²;

если х > 6, то F(x)==

= х=

Таким образом,

График функции F(х) изображен на рис. 5. 3.

Рис. 5.3

в) Р(3≤ Х <5) = F(5)  F(3) = (52)²/16  (32)²/16 = 9/161/16 = =8/16=1/2.

Задача 5.2. Случайная величина Х задана функцией распределения:

Найти дифференциальную функцию распределения f(х).

Решение: Так как f(х)= F’(x), то