Системы обыкновенных дифференциальных уравнений.

§ 1. Нормальные системы.

Определение 1. Нормальная система обыкновенных дифференциальных уравнений имеет следующий вид:

(1.1)

где , – неизвестные функции от независимой переменной x, подлежащие определению; , – известные функции от , заданные и непрерывные в некоторой области. Число n называется порядком системы (1.1). В дальнейшем ограничимся рассмотрением систем второго порядка (n=2).

Определение 2. Пусть дана нормальная система уравнений

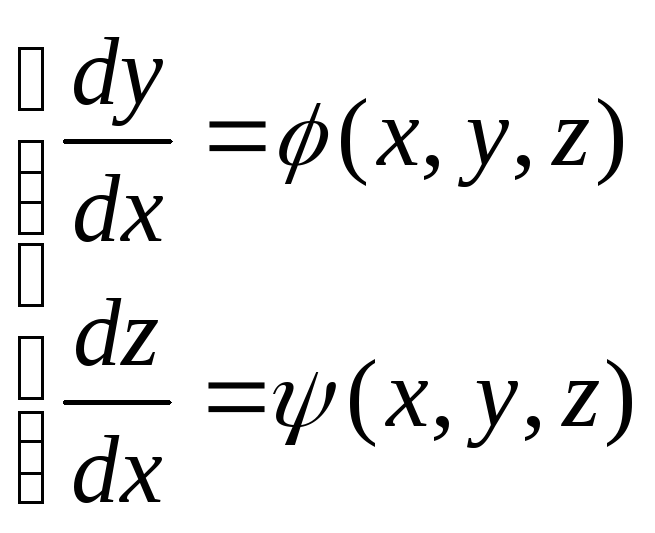(1.2)

где и – заданные и непрерывные в некоторой области функции. Пара функции (y(x); z(x)), определенная на (a,b), имеющая непрерывные производные и удовлетворяющая на (a,b) обоим уравнениям системы (1.2), называется ее решением.

Задача нахождения решения (y(x); z(x)), удовлетворяющего начальным условиям , где – заданные числа (начальные данные), называется задачей Коши.

Теорема существования и единственности решения задачи Коши.

Пусть дана система уравнений (1.2) и пусть в некоторой области D (x,y,z) функции и непрерывны и имеют непрерывные частные производные по y, z. Пусть точка . Тогда существует интервал (a,b) и определенные на нем непрерывно дифференцируемые функции y(x), z(x), удовлетворяющие системе (1.2) и начальным условиям , причем эти функции единственны.

§ 2. Метод исключения.

Продифференцируем, например, первое уравнение системы уравнений (1.2) по независимой переменной x

Вместо системы (1.2) запишем систему уравнений 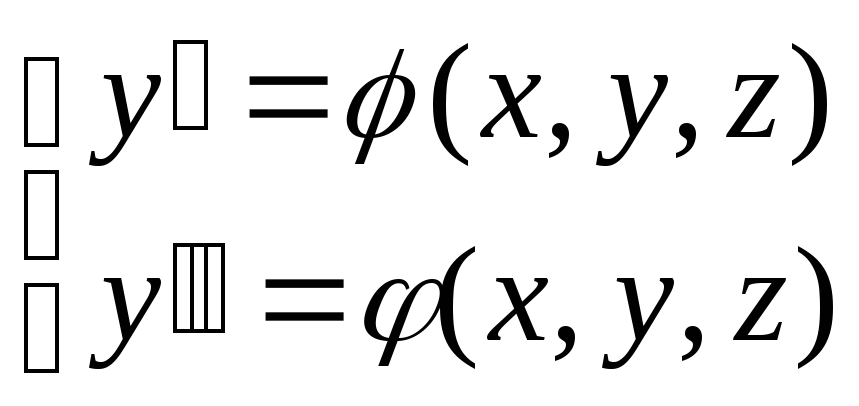(2.1)

(2.1)

Из первого уравнения системы (2.1) следует, что . Подставим эту функцию во второе уравнение (2.1): . Итак, исключив из системы функцию z приходим к одному уравнению 2-го порядка, решая которое, получаем: . Теперь продифференцируем найденное выражение по x и подставим в функцию . И тем самым получим . В результате получим решение в виде:

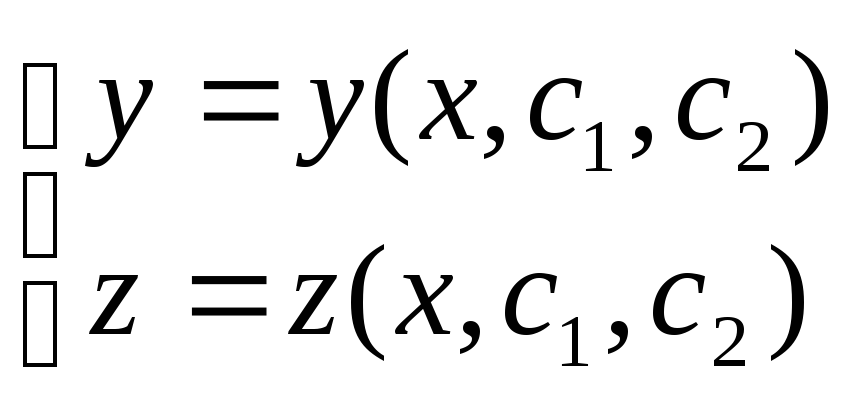(2.2)

Определение 1. Общим решением системы двух обыкновенных дифференциальных уравнений 1-го порядка является совокупность функций (2.2), непрерывно дифференцируемых на некотором интервале (a,b), которые при различных допустимых значениях произвольных постоянных удовлетворяют обоим уравнениям системы уравнений (1.2). При этом в области, в которой выполнены условия теоремы существования и единственности, можно получить решение любой задачи Коши.

§ 3. Линейные однородные системы дифференциальных уравнений (лос ду).

ЛОС ДУ для функции y(x), z(x) называется система уравнений вида

(3.1)

где - непрерывные на (a,b) функции.

Свойства решений ЛОС ДУ (3.1).

1. Сумма двух решений системы (3.1) – тоже решение этой системы.

Доказательство:

Пусть и – два каких-либо решения системы (3.1). Тогда

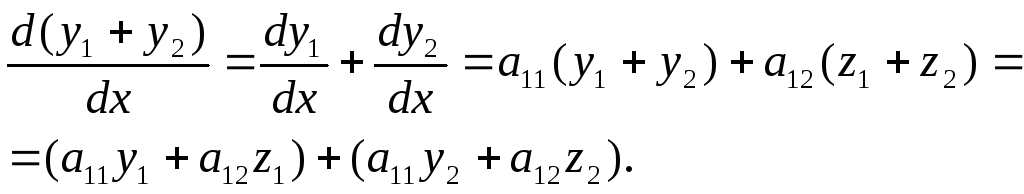
Но и .

Аналогично рассматривается и второе уравнение системы (3.1).

2. Если y(x), z(x) – решение ЛОС ДУ и c – произвольная константа, то cy(x), cz(x) – тоже решение (3.1). Доказательство свойства аналогично доказательству свойства 1.

Следствие.

Если и - решения системы (3.1), то выражение вида

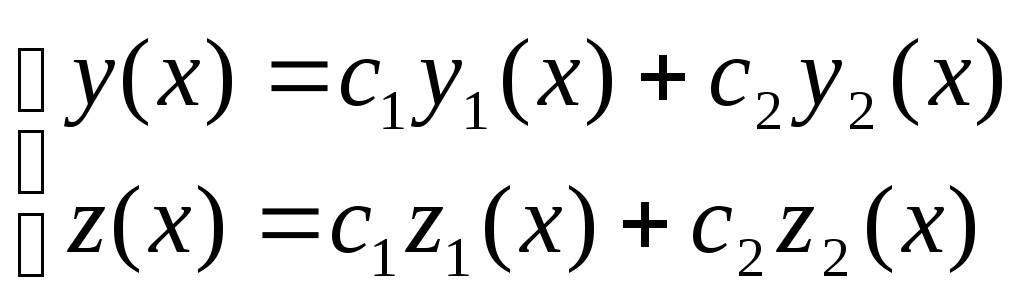
где - произвольные постоянные, тоже решение (3.1).

Определение 1. Система функций и называется линейно независимой на некотором интервале (a,b), если из системы равенств

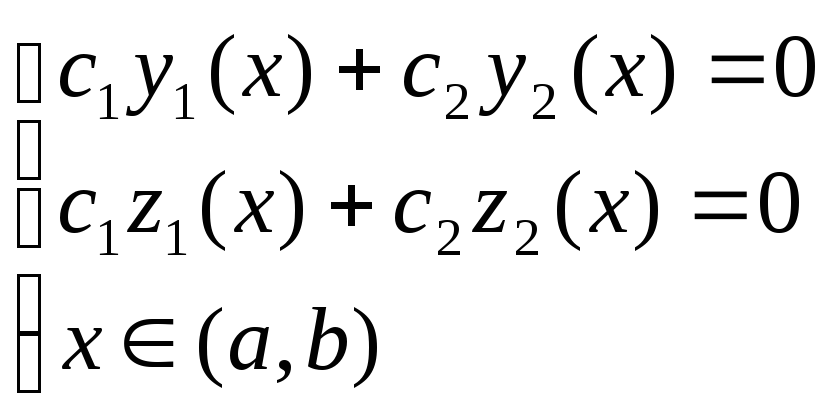(3.2)

Следует, что

В противном случае система функций и - линейно зависима на (a,b).

Определение 2. Определитель, составленный для системы функций и называется определителем Вронского и обозначается W(x). Итак

.

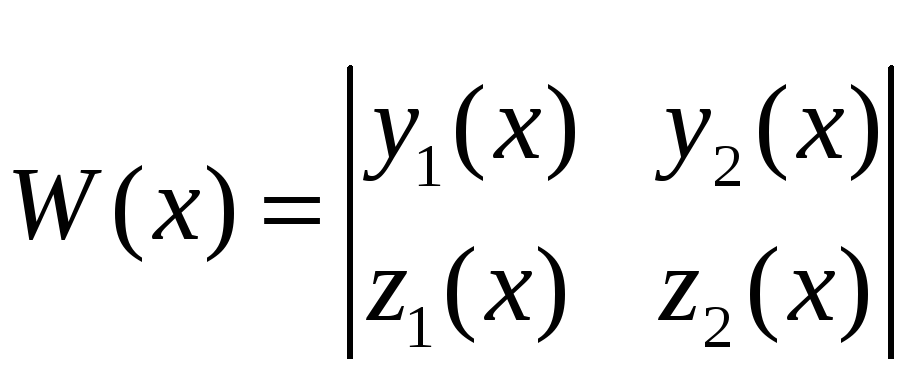Теорема 1. Определитель Вронского для линейно независимой на интервале (a,b) системы решений и ЛОС ДУ не равен нулю ни в одной точке (a,b).

Доказательство.

Докажем теорему методом от противного. Предположим, что существует точка , в которой

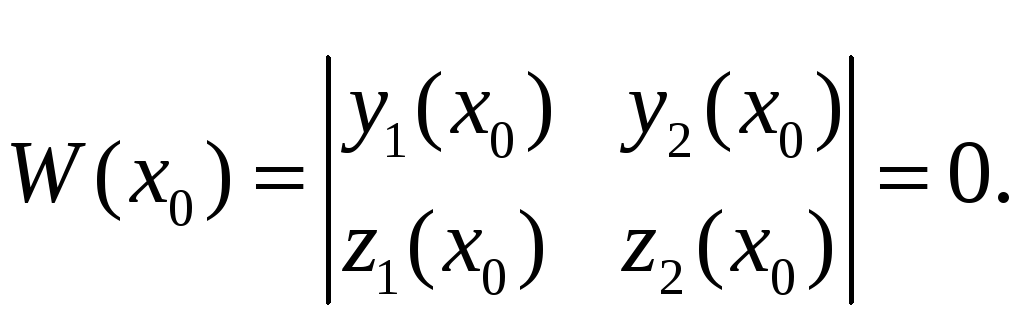
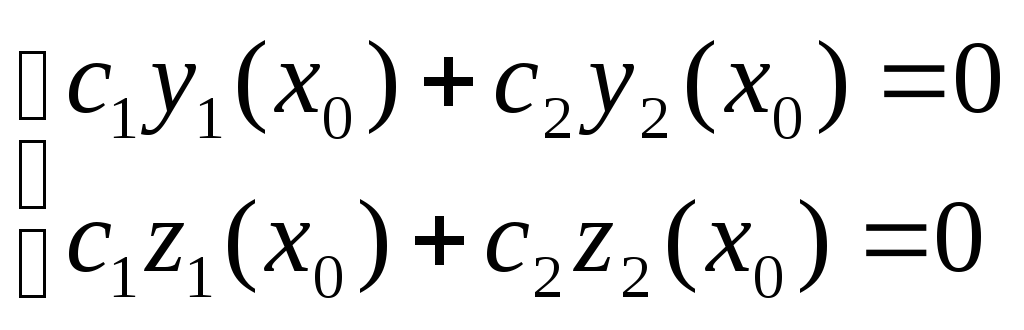Составим линейную однородную систему уравнений с неизвестными  и : (3.3)

Так как определитель системы (3.3) равен нулю, то система имеет бесконечное множество ненулевых решений. Пусть - одно из них. С помощью этих констант и двух линейно независимых на (a,b) решений системы (3.1) и составим две функции

(3.4)

Согласно следствию из свойств решений ЛОС ДУ функции (3.4) являются решениями системы (3.1), которые в силу (3.3) в точке обращаются в нуль. Следовательно, y(x), z(x) – решение следующей задачи Коши:

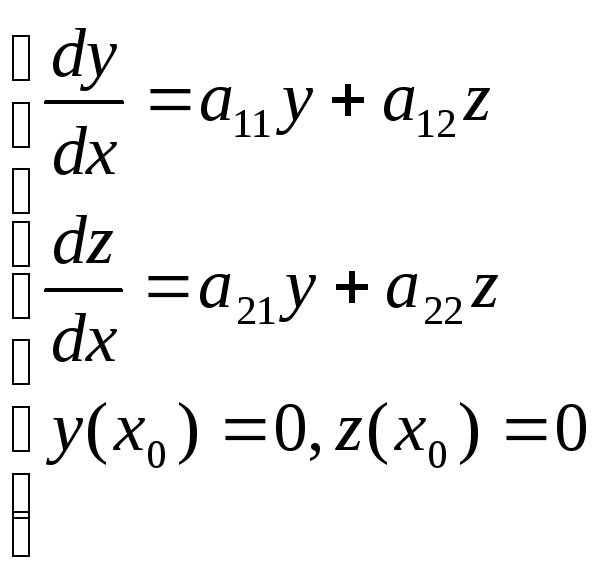
Но таким решением может быть только нулевое решение: y(x)=0, z(x)=0 при , т.е.

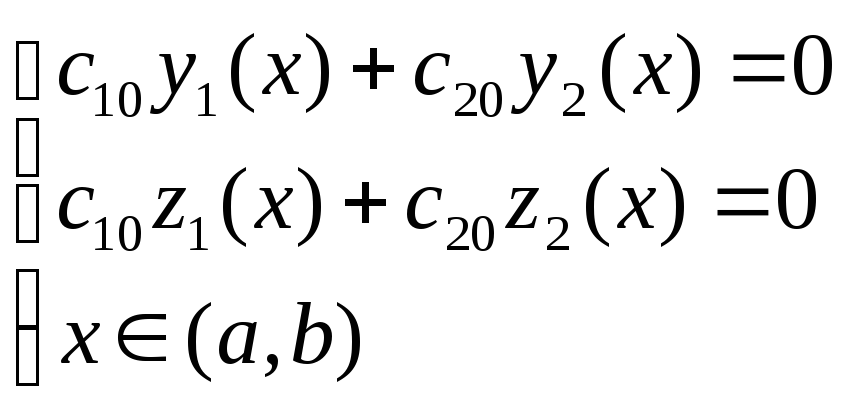
Причем . Это означает, что система функций и линейно зависима на (a,b), что противоречит условию теоремы. Значит наше предположение о существовании на (a,b) точки , в которой , неверно, что и доказывает теорему.

Определение 2. Линейно независимые на (a,b) решения ЛОС ДУ и называются фундаментальной системой решений системы (3.1).

Теорема 2. Если семейство функций и образует фундаментальную систему решений ЛОС ДУ (3.1), то их линейная комбинация

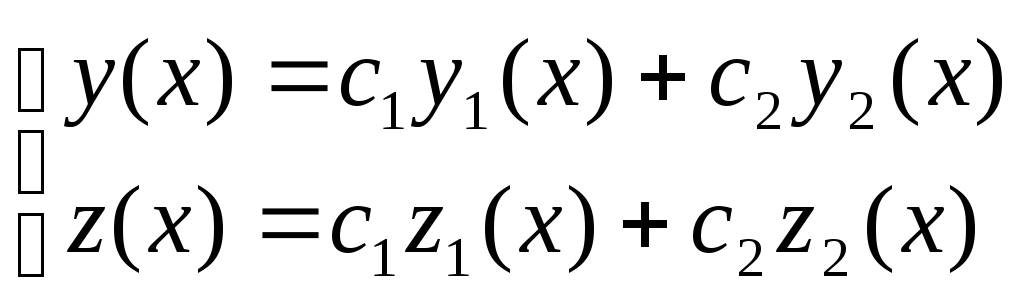, (3.5)

где - произвольные постоянные, дает общее решение системы (3.1)

Доказательство.

1. Выражение (3.5), согласно следствию из свойств решений ЛОС ДУ, является решением системы уравнений (3.1).

2. Докажем, что (3.5) – общее решение (3.1), т.е. докажем, что каковы бы ни были начальные условия задачи Коши 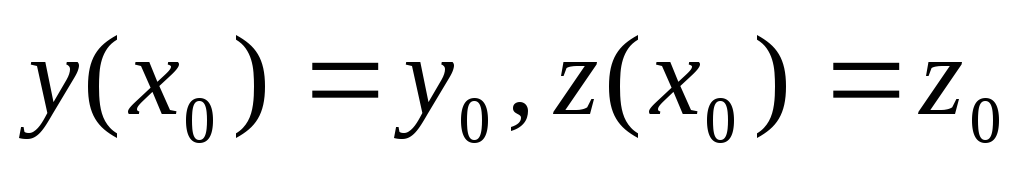, всегда найдутся значения постоянных 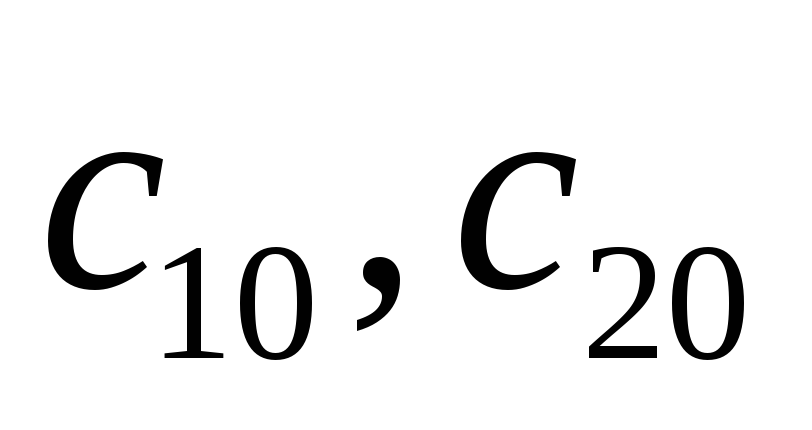такие, что выделенное из общего частное решение ЛОС ДУ:

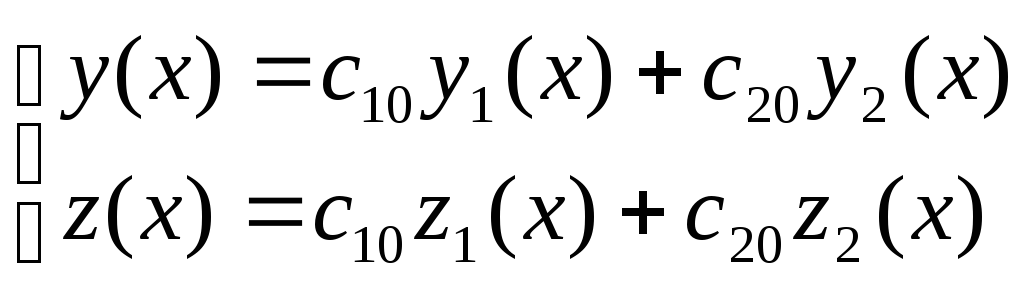
будет удовлетворять этим условиям. Для этого подставим в (3.5) начальные условия:

(3.6)

Определителем этой алгебраической системы линейных уравнений является определитель Вронского :

,

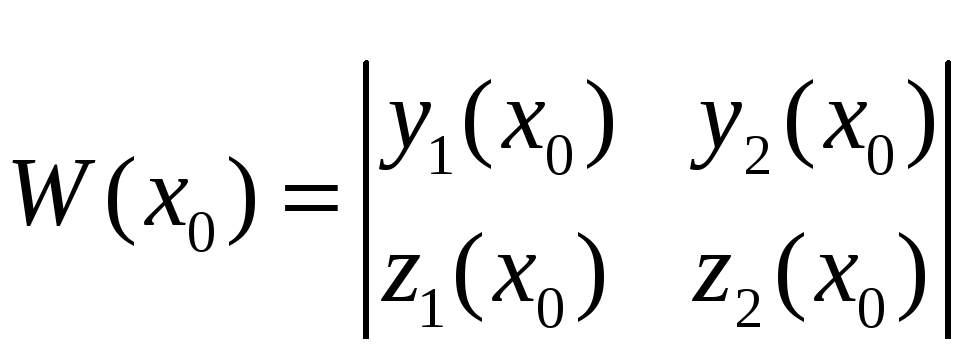который, согласно теореме 1, не равен нулю. Следовательно, система уравнений (3.6) имеет решение и притом единственное.