3.4.2. Метод Гиллеспи

Простым и удобным методом предсказания геометрии молекул является модель отталкивания локализованных электронных пар или метод Гиллеспи, имеющий в своей основе метод ВС. Исходными данными для указанного метода являются число связанных с центральным атомом других атомов, валентные возможности всех связанных атомов, количество электронов на внешнем слое центрального атома. Основные положения метода Гиллеспи сводятся к следующему.

1. Каждая электронная пара, как образующая связь, так и неподеленная, занимает определённое место в пространстве (локализованная электронная пара). Облако двойной и тройной связи рассматривается как единое. Разумеется, электронные пары (электронные облака) отталкиваются.

2. В зависимости от числа локализованных электронных пар (электронных облаков) они располагаются в пространстве следующим образом:

2 – линейная конфигурация,

3 – правильный треугольник,

4 – тетраэдр,

5 – правильная тригональная бипирамида,

6 – октаэдр,

7 – октаэдр с искажением или правильная пентагональная пирамида.

Процедура работы по методу Гиллеспи примерно следующая. Обозначим центральный атом буквой А, любой связанный с ним другой атом – буквой В, неподелённую электронную пару – буквой Е. Пусть общее число партнёров центрального атома по химической связи – n, а число неподелённых электронных пар у него –m. Тогда рассматриваемая молекула в своеобразном свёрнутом виде относительно центрального атома запишетсяAB_nE_m. Разумеется, в качестве центрального атома выбирается самый многовалентный атом. Сложные, громоздкие молекулы в рамках метода Гиллеспи рассматриваются по частям. В результате суммированияnиmпо предложенному выше методу определяется исходная модель геометрии молекулы или иона, а затем после своеобразного отбрасывания неподелённых электронных пар – собственно геометрия частицы.

Возможные дополнения к методу Гиллеспи:

а) облако двойной связи занимает в пространстве бóльшее место, чем облако однократной связи;

б) облако тройной связи занимает в пространстве бóльшее место, чем облако двойной связи и тем более, чем облако однократной связи;

в) в случае полярной ковалентной связи электронное облако сконцентрировано в большей степени возле более электроотрицательного атома;

г) облако неподелённой электронной пары занимает в пространстве бóльшее место, чем облако однократной связи.

Эти дополнения позволяют производить уточнения к геометрии молекул, отклонения от валентных углов, предсказываемых основной процедурой.

Продемонстрируем возможности метода Гиллеспи на примере нескольких молекул. Начнём с разобранных выше молекул воды и аммиака.

Н₂О; АВ₂Е₂;; исходная модель – тетраэдр; молекула – уголковая, угол Н–О–Н 109^о28'.

NH₃; АВ₃Е₁;; исходная модель – тетраэдр; молекула – тригональная пирамида, угол Н–N–Н 109^о28'. Обратим внимание, что тетраэдр, являющийся правильной тригональной пирамидой, более старшая фигура (центральный атом и четыре партнёра по химической связи), чем собственно тригональная пирамида (центральный атом и три партнёра по химической связи).

Еще несколько примеров.

SnCl₂; АВ₂Е₁;; исходная модель – правильный треугольник; молекула – уголковая, уголCl–Sn–Clравен 120^оили меньше в силу того, что свободная электронная пара занимает бóльшее место в пространстве, чем связывающая пара.

СО₂; АВ₂Е₀;; линейная молекула.

Анионы кислот проще всего рассматривать также, как и молекулы самих кислот: H₂SO₄иSO₄^2–AB₄E₀;H₃PO₄иPO₄^3–AB₄E₀;H₂СO₃и СO₃^2–AB₃E₀и т.д.

В ряде случаев возможны несколько моделей строения частиц в рамках метода Гиллеспи, выбирается энергетически более выгодная. Например, XeF₂;AB₂E₃; исходная модель – тригональная пирамида, возможны варианты:

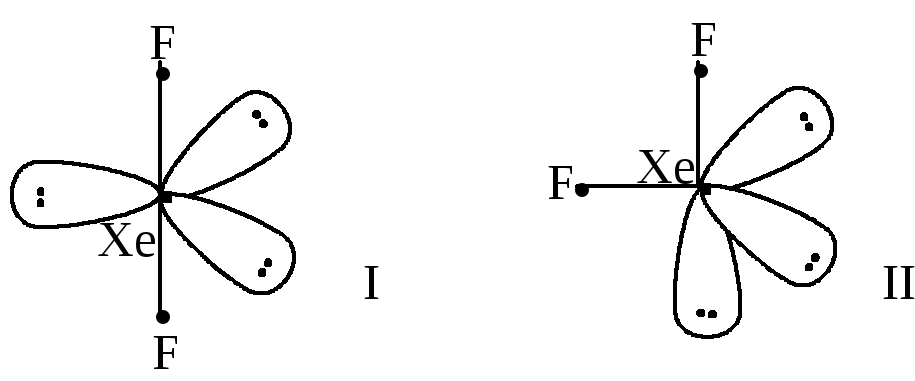
Первый вариант энергетически более выгоден: электронные пары максимально разведены, максимально удалены и атомы фтора, имеющие одинаковые эффективные заряды. Вывод: молекула XeF₂– прямолинейна.