4. Непрерывность и точки разрыва функции

 

 Функция у = f (х) называется непрерывной в точке х₀, если в этой точке бесконечно малому приращению аргумента х-х₀= х соответствует бесконечно малое приращение функции

 у—у₀ = у, т. е. если

lim y = lim [ f (х₀ + х) – f (х₀)] = 0.

Этому определению равносильно следующее:

Функция f (х) называется непрерывной в точке х₀, если при х—> х₀ предел функции существует и равен ее частному значе­нию в этой точке, т. е. если lim f(х) = f (x₀).

 x->х₀

 

Для непрерывности функции f(х) в точке х₀ необходимо и достаточно выполнение следующих условий:

1)функция должна быть определена в некотором интервале, содержащем точку х_0.(т. е. в самой точке х₀ и вблизи этой точки);

2) функция должна иметь одинаковые односторонние пределы

 lim f (х) = lim f (x);

 x->х₀ -0  x->х₀ +0   

3) эти односторонние пределы должны быть равны f (x₀).

Функция f (x) называется разрывной в точке х₀, если она опре­делена в сколь угодно близких точках, но в самой точке х₀ не удовлетворяет хотя бы одному из условий непрерывности.

Разрыв функции f(х) в точке х₀ называется конечным, или 1-го рода, если существуют конечные односторонние пределы

 lim f(x) и lim f(х).

 x-> х₀ -0 x-> х₀ +0

 Все другие случаи разрыва функции называются разрывами- 2-го-рода; в частности, если хотя бы один из указанных односторонних пределов окажется бесконечным, то и разрыв функции называется бесконечным.

Скачком функции f(х) в точке разрыва х₀ называется раз­ность ее односторонних пределов lim f(x) и lim f(х) если они различны.

 x-> х₀ -0  x-> х₀ +0 

Если точка х₀ является левой или правой границей области определения функции f(х), то следует рассматривать значения функции соответственно только справа или только слева от этой точки и в самой точке. При этом:

1) если граничная точка х₀ входит в область определения функции, то она будет точкой непрерывности или точкой раз­рыва функции, смотря по тому, будет ли предел функции при х —>х₀ изнутри ее области определения равен или не равен f(х₀);

2) если граничная точка х₀ не входит в область определения функции, то она является точкой разрыва функции.

Функция называется непрерывной в некотором интервале, если она непрерывна во всех точках этого интервала.

Все элементарные функции непрерывны в тех интервалах, в которых они определены.

5.---

 6. ---

7. Некоторые теоремы о непрерывных функциях.

Теорема 1.

 Если функция y = f(x) представляется в виде суммы постоянного числа b и бесконечно малой :

 y = b+, (1)

то

 (при ).

 Обратно, если , то можно написать , где — бесконечно малая.

 Доказательство. Из равенст­ва (1) следует . Но при произвольном  все значения , начиная с некоторого, удовлетворяют соотношению , следовательно, для всех значений у, начиная с не­которого, будет выполняться неравен­ство . А это и значит, что .

 Обратно: если , то при произвольном  для всех значений у, начиная с некоторого, будет . Но если обозначим , то, следовательно, для всех зна­чений , начиная с некоторого, будет , а это значит, что — бесконечно малая.

 Теорема 2.

 Если стремится к нулю при  (или при ) и не обращается в нуль, тo стремится к бесконечности. 

 Доказательство. 

 При любом, как угодно большом  будет выполняться неравенство , если только бyдет выпол­няться неравенство . Последнее неравенство будет выпол­няться для всех значений , начиная с некоторого, так как . 

 Теорема 3. 

 Алгебраическая сумма двух, трех и вообще определенного числа бесконечно малых есть функция бесконечно малая.

 Доказательство. 

 Проведем  доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится аналогично.

 Пусть , где . Докажем, что при произвольном как угодно малом  найдется  такое, что при удовлетворении неравенства  будет выполняться неравенство . Так как   есть бесконечно малая, то найдется такое  что в окрестности с центром в точке a  в радиусом   будет

 .

Так как есть бесконечно малая, то найдется такое , что в окрестности с центром в точке а и радиусом   будет

 .

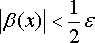 Возьмем  равным меньшему из величин  и , тогда в окрестности точки а с радиусом   будут выполняться неравенства ; . Следовательно, в этой окрестности будет

 .

 т. е. , ч. т. д.

 Аналогично приводится доказательство и для случая, когда

 ,  .

 Теорема  4.

 Произведение функции бесконечно малой  на функцию ограниченную z = z(х)  при  (или ) есть величина (функция) бесконечно малая.

 Доказательство.

 Проведем доказательство для случая . Для некоторого  найдется такая окрестность точки х = а, в которой будет удовлетворяться неравенство . Для всякого  найдется окрестность, в которой будет выполняться неравен­ство . В наименьшей из этих двух окрестностей будет выполняться неравенство

 . 

А это и значит, что —бесконечно малая. Для случая   доказательство проводится аналогично.

 Из данной теоремы вытекают:

 Следствие  1. Если , lim=0, тo  lim=0, так как   есть величина ограниченная. Это справедливо для любого конечного числа множителей. 

 Следствие  2. Если  и c = const, то lim ca = 0.

 

Теорема  5.

 Частное  от деления величины бесконечно малой(х) на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

 Доказательство.

 Пусть На основании теоремы, что 1/ есть величина ограни­ченная. Поэтому дробь  есть произведение величины бесконечно малой на величину ограниченную, т. е. величина беско­нечно малая.

 Бесконечно малые функции  и  называются эквивалентными, если . Эквивалентность обозначается символом “~”, т.е. пишут ~ .