Вопросы по Высшей математике.

1.Предел Числовой последовательности.

2. Свойства пределов числовой последовательности (с доказательством).

3.Предел функции.

4.Непрерывность функции. Точки разрыва.

5.Точки разрыва, пределы слева и справа.

6. Теорема о единственности предела(с доказательством).

7. Некоторые теоремы о непрерывных функциях.

8.Бесконечно малые и бесконечно большие величины.

9. Связь между пределом функции и бесконечно малой величиной.

10. Свойства пределов функции (с доказательством).

11. 1-ый замечательный предел (с доказательством).

12. 2-ой замечательный предел( с доказательством того, что 2<lim).

13. 2-ой замечательный предел( с доказательством того, что lim<3).

14. Определение производной, физический и геометрический смысл.

15. Связь между непрерывностью и дифференцированностью(с доказательством ).

16.Дифференциал от функции, производные высших порядков, таблица производных.

Ответы

1.Предел Числовой последовательности.

Функция f(x) называется функцией целочисленного аргумента, если множество значений x, для которых она определена, является множеством всех натуральных чисел1, 2, 3,… Примером функции целочисленного аргумента может служить сумма n первых чисел натурального ряда. В данном случае

Числовой последовательностью называется бесконечное множество чисел

  (1)

следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого  задается как функция целочисленного аргумента,  т.е.  .

Число А называется пределом последовательности (1), если для любого   существует число  , такое, что при  выполняется неравенство  . Если число А есть предел последовательности (1), то пишут

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.

Для сходящихся последовательностей имеют место теоремы:

 если  .

2. Свойства пределов числовой последовательности

Арифметические свойства

А)

 Б)

В)

Г)

Свойства сохранения порядка

Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа.

Если некоторое число не превышает все элементы сходящейся последовательности, начиная с некоторого номера, то оно также не превышает и предела этой последовательности.

Если некоторое число строго превышает все элементы сходящейся последовательности, начиная с некоторого номера, то предел этой последовательности не превышает этого числа.

Если все элементы сходящейся последовательности, начиная с некоторого номера, строго превышают некоторое число, то это число не превышает предела этой последовательности.

Если, начиная с некоторого номера, все элементы одной сходящейся последовательности не превышают соответствующих элементов другой сходящейся последовательности, то и предел первой последовательности не превышает предела второй.

Для числовых последовательностей справедлива теорема о двух милиционерах (принцип двустороннего ограничения).

3. Предел функции

 Рассмотрим  некоторые случаи изменения функции при стремлении аргумента х к некоторому пределу а или к бесконечности.

 Определение 1. Пусть функция  определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция  стремится к пределу  при х, стремящемся к , если для каждого положительного числа , как бы мало оно ни было, можно указать такое положительное число , что для всех х, отличных от   и удовлетворяющих неравенству , имеет место неравенство

 .

Если  есть предел функции f(x) при , то пишут:илиf (x) при .

 Если  при , то на графике функции , т.к. из неравенства  следует неравенство , то это значит, что для всех точек х, отстоящих от точки  не далее чем на , точки М  графика функции  лежат внутри полосы шириной , ограниченной прямыми   и (рис. 2).

 

  Рассмотрим переменную величину у = f (х). При этом считать, как и всюду в дальнейшем, что из двух значений  функции последующим является то значение, которое соответствует последующему значению аргумента. Если определенная так переменная величина у при  стремится к некоторому пределу , то будем писать

 

и говорить, что функция у = f (х) стремится к пределу b при .

 Легко доказать, что оба определения предела функции эквива­лентны. Замечание.

 Если f (x) стремится к пределу b₁ при х, стре­мящемся к некоторому числу  так, что x принимает только значения, меньшие , то пишут  и называют b₁ пределом функ­ции f(x) в точке  слева. Если х при­нимает только значения большие, чем , то пишут  и называют b₂, пределом функции в точке   справа.

 Можно доказать, что если, предел справа и предел слева существуют и равны, т. е. , то b и будет пределом в смысле данного выше оп­ределения предела в точке . И об­ратно, если предел функции b в точке , то существуют пределы функции в точке   справа и слева и они равны.

 Замечание.

 Для существования предела функции при  не требуется, чтобы функция была определена в точке . При нахождении предела рассматриваются значения функции в окрестности точки , отличные от ; это положение наглядно иллю­стрируется следующим примером.

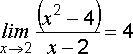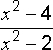 Пример.  Докажем, что . Здесь функция  не определена при х = 2.

 Нужно  доказать, что при произвольном  найдется такое , что будет выполняться неравенство 

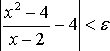 , (1)

если | х — 2 | < . Но при х2 неравенство (1) эквивалентно неравенству

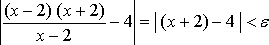 (2)

или .

Таким  образом, при произвольном  неравенство (1) будет выполняться, если будет выполняться неравенство (2) (здесь  ). А это и значит, что данная функция при  имеет пределом число 4.

Рассмотрим  некоторые случаи изменения функции при . Определение 2. Функция f(x) стремится к пределу , если для каждого произвольно малого положительного числа  можно указать такое положитель­ное число N, что для всех значении х, удовлетворяющих неравенст­ву , будет выполняться неравенство .

  Зная смысл символов:  очевидным является и смысл выражений:

 стремится к b при  и

 стремится к b при ,

 которые символически записываются так:

 ,