3. Метод Симпсона

Метод базируется на замене подынтегральной функции квадратичной параболой, которая строится уже не по двум (как прямая в методе трапеций), а по трем точкам на каждом участке. По этим трем точкам (крайние точки участка и средняя точка) строится интерполяционная функция – полином второго порядка, который аналитически интегрируется. Получается следующая расчетная формула:

1.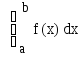

I = ≈ h/3(f(x₀) + 4f(x₁ ) +f(x₂ ))

w₀ = w₂ = h/3 w₁ = 4h/3

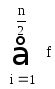
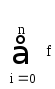x₀ = a x₁ = (b-a)/2 x₂ = b h=(b-a)/2

2.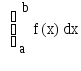

I = ≈ ((h(f(x₀))/3) + (4h/3 (x_2i-1) + 2h/3 (x_2i ) + (h*f(x_n )/3) = w_i f(x_i )

w₀ = w_n = h/3 w₂ = w₄ = … = w_n-2 =2h/3

w₁ = w₃ = … =w_n-1 = 4h/3

В этой формуле все ординаты с нечетными номерами имеют коэффициент 4h/3, а с четными – 2h/3 (кроме нулевого и последнего). При работе с этим методом обязательно разбивают весь интервал на четное число участков.

По сравнению с методами прямоугольников и трапеций он более точный (подынтегральная функция почти совпадает с параболой).

Метод Симпсона обеспечивает вычисление интеграла точно, без погрешности при полиноме третьего порядка. Следовательно, этот метод предпочтительнее предыдущих.

Оценить по грешность при использовании двойного просчета можно по соотношению

R≤ (|I_n–I_n/2|)/15

т.е. при увеличении числа разбиений в два раза погрешность падает в 15 раз.

Теоретические формулы оценки погрешности содержат производную четвертого порядка от подынтегральной функции, поэтому не имеют практического значения.

Пример 5.3. Рассмотрим вычисление интеграла из предыдущего раздела.

1) x₀ = 0x₁ = 0,5x₂ = 1h= 0,5

I= (0,5/3)((1/(1+0)) + ((4*1)/(1+0.5²)) + (1/1+1²) = 0,7833333

2) x₀ = 0x₁ = 0.25x₂ =0.5 x₃ = 0.75 x₄ = 1 h = 0.25

I = (0.25/3)*(1/(1+0)) + ((4*0.25)/3)*(1/(1+0.25² )) + ((2*0.25)/3)*(1/(1.05²)) + +((4*0.25)/3)*(1/(1+0.75²)) + ((0.25/3)*(1/(1+1)) = 0.78539216

Пример. 5.4. Вычислить интеграл: .

1. Вычислим I₁₆и I₈по формулам Симпсона.

Формулы для вычислений:

n=16:

n=8:

Вычисления выполним в табличном процессоре Excel.

2. I=(I₁₆+I₈)/20,404 13

3. Оценим точность вычислений по правилу удвоения:

Формула для оценки точности:

т.о. требуемая точность достигнута.

ОТВЕТ:

4. Метод Ньютона-Koтeca

Данный метод является обобщением предыдущих, построен на аналогичных принципах и предполагает замену подынтегральной функции параболой k-го порядка (а не второго, как в методе Симпсона). Расчетная формула для одного (!) участка выглядит следующим образом:

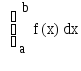
I = = (b-a)* (x_i)* H_i

w_i = (b-a)* H_i

где x₀=a,x_k=b,x₁=a+i*(b-a)/k,H_i– коэффициенты Ньютона–Котеса, аk– число использующихся ординат на участке (начиная с 0), которые применяются для аппроксимации подынтегральной функции. Естественно, что для заменыf(x) параболой третьей степени потребуется уже четыре точки, а четвертой – пять точек. КоэффициентыH_i, не зависят от функцииf(x) и определены заранее. Некоторые из них приведены ниже.

k=1;H₀=H₁=1/2;

k=2;H₀=H₂=1/6;H₁=2/3;

k=3;H₀=H₃=1/8;H₁=H₂=3/8;

k=4;H₀=H₄=7/90;H₁=H₃=16/45;H₂=2/15;

k=5;H₀=H₅=19/288;H₁=H₄=25/96;H₂=H₃=25/144.

…

Все предыдущие формулы являются частным случаем формулы Ньютона–Котеса. В частности, при k= 1 получаем метод трапеций (для одного участка), приk=2 - формулу Симпсона. Не следует братьk>10, так как при больших значенияхkалгоритм оказывается неустойчивым.

При разбиении всего интервала [а, b] наnучастков формулу нужно применять для каждого участка, а результаты сложить.

Пример 5.5.

Рассмотрим вычисление интеграла из предыдущего раздела. Выберем k= 4.

1) k=4 1 отрезок

I= 7/90*f(0) + 16/45*f(0.25) + 2/15*f(0.5) + 16/45*f(0.75) + 7/90*f(1) = 0.875294

2) в этом случае разобьем интервал на четыре участка (n= 4) сh=0,25, применим для каждого интервала формулу сk= 4, сложим результаты и получимI= 0,78539817.