
- •Исследование теплоотдачи цилиндра
- •Содержание
- •Введение
- •Задачи и цель работы
- •3. Описание экспериментальной установки и методики измерений
- •4. Порядок проведения опытов
- •5. Обработка опытных данных по конвективному теплообмену
- •6. Расчет статистических показателей
- •7. Приложения Определение расхода воздуха через установку
- •Расчет погрешностей измерений
- •Специальность_______________________Курс, группа___________________
- •В о п р о с ы для самоконтроля по курсовой работе "Исследование теплоотдачи цилиндра в закрученном потоке"
- •1. Теоретические основы обоснования метода исследования:
- •2. Экспериментальный стенд по исследованию теплоотдачи цилиндра в закрученном потоке:
- •3. Обработка результатов исследования:
- •Сергей Васильевич карпов
6. Расчет статистических показателей
После определения
величин n,
A
рассчитывают статистические показатели,
характеризующие разброс экспериментальных
точек относительно линии регрессии, а
также тесноту и достоверностьустановленной
связи между
 и
и .
Общая дисперсия (рассеивание) точек
относительно среднеарифметического
значения
.
Общая дисперсия (рассеивание) точек
относительно среднеарифметического
значения
 для опытов определяется по уравнению
для опытов определяется по уравнению
 .
(14)
.
(14)
Дисперсия точек относительно линии регрессии:
 (15)
(15)
где
 - дисперсия относительно среднего
значения lgNu
- дисперсия относительно среднего
значения lgNu
 .
.
Извлекая
квадратный корень из дисперии
 получают величину
среднеквадратичного отклонения
экспериментальных точек от прямой линии
регрессии, называемую иначе стандартом
отклонения. Для определения погрешностей
опытов и расчётов по уравнению подобия
(границ доверительной вероятности)
задаются коэффициентом надёжности
(доверительной вероятности) P.
В практике научно-технических расчетов
рекомендуется принимать P
= 0,95. Границы
доверительного интервала по Nu
оцениваются уравнением
получают величину
среднеквадратичного отклонения
экспериментальных точек от прямой линии
регрессии, называемую иначе стандартом
отклонения. Для определения погрешностей
опытов и расчётов по уравнению подобия
(границ доверительной вероятности)
задаются коэффициентом надёжности
(доверительной вероятности) P.
В практике научно-технических расчетов
рекомендуется принимать P
= 0,95. Границы
доверительного интервала по Nu
оцениваются уравнением
 ,
(16)
,
(16)
где
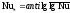 ;tα
- коэффициент Стьюдента, определяемый
по табл. 4 [11] в зависимости от величины
выборки (числа опытов);
;tα
- коэффициент Стьюдента, определяемый
по табл. 4 [11] в зависимости от величины
выборки (числа опытов);
Относительная величина отклонения опытных точек от расчетной зависимости:
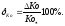 (17)
(17)
Характеристикой
тесноты и достоверности связи между
величинами Nu
и Reвх
является коэффициент корреляции

 . (18)
. (18)
Значения
 могут находиться
в пределах от 0 до ± 1, причём знак
могут находиться
в пределах от 0 до ± 1, причём знак должен соответствовать
знаку углового коэффициента прямой
линии регрессии по уравнению (11). Чем
ближе значение
должен соответствовать
знаку углового коэффициента прямой
линии регрессии по уравнению (11). Чем
ближе значение
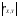 к единице, тем
более тесной является прямолинейная
связь между
к единице, тем
более тесной является прямолинейная
связь между
 и
и в логарифмической
анаморфозе. Заметим, что в предельном
случае при
в логарифмической
анаморфозе. Заметим, что в предельном
случае при
 =
0 такая связь полностью отсутствует.
=
0 такая связь полностью отсутствует.
Оценка достоверности прямолинейной связи производится исходя из необходимости выполнения условия
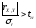 ,
(19)
,
(19)
где
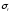 -
среднеквадратичная погрешность
коэффициента корреляции, вычисляемая
по приближенной зависимости
-
среднеквадратичная погрешность
коэффициента корреляции, вычисляемая
по приближенной зависимости
 ,
(20)
,
(20)
tα - коэффициент Стьюдента, принимаемый по данным табл.1.
Таблица 1
Значения коэффициента Стьюдента tα
при доверительной вероятности P = 0,95
|
z-1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
tα |
12,71 |
4,30 |
3,18 |
2,78 |
2,57 |
2,45 |
2,36 |
2,31 |
2,26 |
|
z-1 |
10 |
15 |
29 |
30 |
50 |
100 |
- |
- |
- |
|
tα |
2,23 |
2,13 |
2,09 |
2,04 |
2,01 |
1,98 |
- |
- |
- |
7. Приложения Определение расхода воздуха через установку
Модуль сужающего отверстия
 (21)
(21)
где d – диаметр отверстия нормальной диафрагмы, мм; Dтр – диаметр измерительного трубопровода, мм.
Плотность воздуха перед сужающим устройством
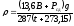 кг/м3,
(22)
кг/м3,
(22)
где В – барометрическое давление, мм.рт.ст; Pс.д, мм.вод.ст; g - ускорение силы тяжести, g = 9,80665 м/с2; t - °C.
Поправочный множитель на расширение измеряемой среды ε для нормальных диафрагм определяется зависимостью [11]
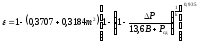 ,
(23)
,
(23)
где P – перепад давления на диафрагме, мм.рт.ст; k - показатель адиабаты измеряемой среды (для воздуха k = 1,4). При измерении P дифференциальными микроманометрами, например типа ММН-240, величину перепада давления определяют по следующей формуле:
 мм вод.ст.,
(24)
мм вод.ст.,
(24)
где ρж - плотность рабочей жидкости микроманометра (спирта) при 20°С, г/см3; 0,8095 - плотность эталонного спирта при 20°С, г/см3; 0,0011 - коэффициент объемного расширения спирта, 1/°С; tж - температура рабочей жидкости, принимаемая равной tос; kизм - множитель, равный синусу угла наклона измерительной трубки микроманометра; Нпок - показание прибора, отсчитываемое по измерительной шкале, мм.
Теоретический расход воздуха через экспериментальную установку
 м3/с,
(25)
м3/с,
(25)
где αи - исходный коэффициент расхода; k2 - поправочный множитель на шероховатость измерительного трубопровода; k3 - поправочный множитель на неостроту входной кромки диафрагмы; d – в мм.
Значение αи зависит от типа сужающего устройства и модуля m:
при
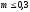
 ;
(26)
;
(26)
при
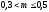
 (27)
(27)
при

 (28)
(28)
Произведение поправочных множителей k2,3 = k2k3 находят из таблицы 2 [11] по значениям m, Dтр.
Таблица 2
Произведение поправочных множителей k2,3
|
Dтр, мм |
Значение коэффициента k2,3 при m | ||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 | |
|
50 100 150 200 250 |
1,023 1,017 1,012 1,008 1,005 |
1,022 1,014 1,010 1,005 1,003 |
1,023 1,013 1,008 1,004 1,002 |
1,024 1,014 1,008 1,004 1,002 |
1,025 1,015 1,008 1,005 1,002 |
1,028 1,017 1,010 1,005 1,003 |
1,031 1,019 1,011 1,007 1,004 |
Коэффициент кинематической вязкости воздуха рассчитывают, используя известную формулу Милликена
 м2/с.
(29)
м2/с.
(29)
Число Рейнольдса, отнесенное к диаметру измерительного трубопровода
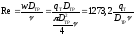 .
(30)
.
(30)
Действительный расход воздуха
 м3/с,
(31)
м3/с,
(31)
где k1 - поправочный множитель на число Рейнольдса, определяемый по номограмме, представленной на рис.4 [11].
Рис.4. Поправочный множитель к коэффициенту расхода при Re < Reпред
Предельное число Рейнольдса Reпред, начиная с которого коэффициент расхода α = αиk1k2k3 не зависит от него (k1 = 1), находят в зависимости от m и типа сужающего устройства по табл. 3.
Для основной диафрагмы, используемой на стенде (m= 0,259), k1 можно рассчитать также по приближенному аппроксимационному уравнению
 .
(32)
.
(32)
Плотность воздуха во входных каналах циклонной камеры
 кг/м3.
(33)
кг/м3.
(33)
Среднерасходная скорость воздуха в шлицах
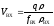 м/с.
(34)
м/с.
(34)
Коэффициент кинематической вязкости воздуха при входных условиях
 м2/c.
(35)
м2/c.
(35)
Входное число Рейнольдса вычисляется по формуле
 .
(36)
.
(36)
