5. Обработка опытных данных по конвективному теплообмену

Суммарный тепловой поток от калориметра к охлаждающему воздуху определяется по количеству конденсата², собранному за время опыта с рабочего участка:

Вт, (2)

где G_К – масса конденсата, кг;

τ – время опыта, с;

r_n – удельная теплота парообразования, Дж/кг.

Значение r_n можно определить по таблицам насыщения воды и водяного пара [12], зная температуру насыщения t_н. Последняя, в свою очередь, определяется величиной абсолютного давления пара в калориметре. В рабочем диапазоне P_абс = 735…875 мм рт.ст. (98…116,7 кПа) табличная зависимость температуры насыщения от давления может быть аппроксимирована уравнением

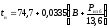⁰С, (3)

где Р_изб – избыточное давление в калориметре, создаваемое столбом конденсата в гидрозатворе, Р_изб =Н_гидр, мм вод.ст.

В диапазоне t_н = 102…104 ⁰С табличные данные [12] по r_п обобщаются зависимостью

Дж/кг. (4)

Лучистый тепловой поток между калориметром и боковой поверхностью циклонной камеры рассчитывается по уравнению Стефана-Больцмана

, (Вт) (5)

где - приведенная степень черноты системы; ε_ц, ε_ст - соответственно степени черноты калориметра и поверхности циклонной камеры(,); C₀=5,77 - постоянная Стефана-Больцмана, ;Т_ц - абсолютная температура внешней поверхности калориметра , К; T_ст - абсолютная температура внутренней поверхности камеры ();F_ц - площадь поверхности теплообмена калориметра, F_ц=πd_цl_ц, м²; F_ст - площадь боковой поверхности циклонной камеры, , м².

Температуру поверхности теплообмена калориметра t_ц можно принять равной t_н, так как уровень теплоотдачи при конденсации пара внутри калориметра на его внутренней поверхности во много десятков раз превышает уровень теплоотдачи от его внешней поверхности к закрученному потоку воздуха. Следовательно, термическим сопротивлением теплоотдачи при конденсации пара можно пренебречь. Термическим сопротивлением теплопроводности стенки калориметра, учитывая её малую толщину и высокий коэффициент теплопроводности материала, также можно пренебречь. Погрешность, вызванная подобными допущениями, как показывают расчеты, для большинства случаев не превышает 0,5…1 %.

Зная величину Q_л, можно определить конвективный тепловой поток

Вт. (6)

Коэффициент теплоотдачи конвекцией от калориметра к закрученному воздуху определяется по уравнению Ньютона-Рихмана

Вт/(м^{2 0}С). (7)

Число Нуссельта

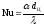, (8)

где 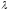- коэффициент теплопроводности воздуха при входной температуре потока определяют по справочным таблицам либо рассчитывают по аппроксимационной зависимости, справедливой в диапазоне температурt_вх = 10…40 ⁰С

Вт/(м^°С). (9)

Результаты расчетов записываются в табл. 3 Приложения.

После обработки опытных данных по теплоотдаче для всех исследованных в работе режимов по числу Рейнольдса (не менее 4…6) в пределах каждой серии опытов (характеризуемой определенным сочетанием геометрических характеристик циклонной камеры) устанавливается функциональная связь между числами Nu и Re_вх в виде зависимости

, (10)

где A, n – постоянные. Для нахождения коэффициентов A, n в уравнении подобия (10) результаты опытов представляют графически в координатах lg Nu- lg Re_вх (рис.3).

Рис.3. К обработке опытных данных по теплоотдаче цилиндра в закрученном циклонном потоке, определение показателя степени при Re_вх: □ – опытные точки; линия – расчетная зависимость

Тангенс угла наклона прямой относительно оси Re_вх определяет показатель степени n у числа Re_вх. Действительно, прологарифмировав уравнение (10), получим

. (11)

Последнее выражение является уравнением прямой.

Значение n определяют графически, проведя линию через опытные точки таким образом, чтобы обеспечить наилучшее соответствие экспериментальным данным. Этот простейший метод обработки называют методом «натянутой нити».

Наиболее обоснованным и широко распространенным в практике научных исследований видом аппроксимации опытных данных является метод "наименьших квадратов", связанный со статистическим законом распределения случайных ошибок эксперимента.

Сущность метода заключается в том, что он обеспечивает минимальное значение суммы квадратов отклонений опытных точек по вертикали от расчетной зависимости, описывающей экспериментальные данные. Изложение теории метода наименьших квадратов можно найти в специальной литературе, например в работе [13].

Применим данный метод для окончательной обработки результатов экспериментов. Исходя из среднеарифметических значений ³ирасчётные соотношения для коэффициентовn, A имеют вид

(12)

, (13)

где ;, гдеz – число опытов.

Для удобства вычислений результаты промежуточных расчётов заносят в табл.4 Приложения.

По полученным значениям n, A строят линию регрессии, соответствующую уравнению (11), как показано на рис.3.