Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северный (Арктический) федеральный университет им. М. В. Ломоносова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Хорошие лекции

.pdf

Скачиваний:

Добавлен:

13.02.2015

Размер:

695.43 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 33

Будем постепенно увеличивать число каналов (телефонных номеров) n = 2, 3, 4,... и

определим для получаемой n -канальной СМО характеристики обслуживания. Значения характеристик СМО сведем в таблицу.

Показатели эффективности	Обозначение	Число каналов (телефонных номеров)

		1	2	3	4	5	6


Относительная пропускная	Q	0,25	0,47	0,65	0,79	0,90	0,95
способность


Абсолютная пропускная	A	22,5	42,3	58,8	71,5	80,1	85,3
способность


По условию оптимальности Q ≥ 0,9 , следовательно, в фирме необходимо установить
5 телефонных номеров (в этом случае Q = 0,90 ). При этом в час будут обслуживаться в

среднем 80 заявок ( A =80,1), а среднее число занятых телефонных номеров (каналов) k =

A μ =80,1 30 ≈ 2,67 .

Тут уже проглядывает некоторый намек на оптимизацию. В самом деле, содержание каждого канала в единицу времени обходится в какую-то сумму. Вместе с тем, каждая обслуженная заявка приносит какой-то доход (если речь идет о СМО, для которых этот доход можно оценить). Умножая этот доход на среднее число заявок A , обслуживаемых в единицу времени, мы получим средний доход от СМО в единицу времени. Естественно, при увеличении числа каналов этот доход растет, но растут и расходы, связанные с содержанием каналов. Что перевесит – увеличение доходов или расходов? Это зависит от условий операции, т.е. от «платы за обслуживание заявки» и от стоимости содержания канала. Зная эти величины, можно найти оптимальное число каналов, наиболее экономически эффективное.

СМО с ожиданием (с очередью)

1. Одноканальная СМО с ожиданием и ограничением на длину очереди. На прак-

тике довольно часто встречаются одноканальные СМО с очередью (врач, обслуживающий пациентов; кассир, выдающий зарплату; телефон-автомат на улице и т.д.). В теории массового обслуживания одноканальные СМО с очередью также занимают особое место: именно к таким СМО относится большинство полученных до сих пор аналитических формул для немарковских систем.

Рассмотрим одноканальную СМО, на вход которой поступает простейший поток заявок с интенсивностью λ. Предположим, что поток обслуживаний также простейший с интенсивностью μ . Это означает, что непрерывно занятый канал обслуживает в среднем μ

заявок в единицу времени. Заявка, поступившая в СМО в момент, когда канал занят, в отличие от СМО с отказами, не покидает систему, а становится в очередь и ожидает обслуживания.

Далее предполагаем, что в данной системе имеется ограничение на длину очереди, под которой понимается максимальное число мест в очереди, а именно, предполагаем, что в очереди могут находиться максимум m ≥1 заявок. Поэтому заявка, пришедшая на вход СМО, в момент, когда в очереди уже стоят m заявок, получает отказ и покидает систему необслуженной.

Таким образом, рассматриваемая СМО относится к системам смешанного типа с ог-

раничением на длину очереди.

Пронумеруем состояния СМО по числу заявок, находящихся в системе, т.е. под обслуживанием и в очереди:

S0 – канал свободен (следовательно, очереди нет);

S1 – канал занят и очереди нет, т.е. в СМО находится (под обслуживанием) одна заявка; S2 – канал занят и в очереди стоит одна заявка;

……………………………………………………..

Sm+1 – канал занят и в очереди m заявок.

Граф состояний данной СМО представлен на рис. 10 и совпадает с графом , описывающим процесс гибели и размножения, с тем отличием, что при наличии только одного канала обслуживания все интенсивности потоков обслуживаний равны μ .

...

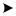λμSm+1

Рисунок 10.

Для описания предельного режима работы СМО можно воспользоваться изложенными ранее правилами и формулами. Запишем сразу выражения, определяющие предельные вероятности состояний:

p	k	=	ρk p	0	, k		=1,2,..., m +1,

						2	m +1 −1
		=	(1+ ρ + ρ				+... + ρ	) ,
p0
где ρ =λ μ – интенсивность нагрузки канала.
Если λ = μ, то получаем p0			= p1 =... = pm +1 =1 (m + 2) .
Пусть теперь λ ≠ μ ( ρ ≠1). Выражение для p0								можно в данном случае записать

проще, пользуясь тем, что в знаменателе стоит сумма m + 2 членов геометрической прогрессии со знаменателем ρ :

p		=		1	− ρ	.
	0		1 −		ρ m +2

Заметим, что при m = 0 мы переходим к уже рассмотренной одноканальной СМО с отказами. В этом случае p0 =(1 − ρ)(1 − ρ2 ) = μ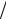(λ + μ) (как и было получено ранее).

Определим основные характеристики одноканальной СМО с ожиданием: относительную и абсолютную пропускную способность, вероятность отказа, а также среднюю длину очереди и среднее время ожидания заявки в очереди.

Поступившая на вход СМО заявка получает отказ тогда и только тогда, когда канал

занят и в очереди ожидают m заявок,			т.е. когда система находится в состоянии S m +1 . По-
этому вероятность отказа определяется вероятностью появления состояния S m +1 :
		ρ m +1 (1 − ρ)				,	если	ρ ≠1;

			1 − ρ		m +2
Pотк	= pm +1		1 − ρ
Pотк	= pm +1	=	1
			1	,			если	ρ =1.
				,			если	ρ =1.
		m + 2

Относительная пропускная способность, или доля обслуживаемых заявок, поступающих в единицу времени, определяется выражением:

	1− ρ m +1
					,
		− ρ	m +2
Q =1− Pотк	1
	=
	m +1			,

	m +2

если	ρ ≠1;
если	ρ =1.

Заметим, что относительная пропускная способность Q совпадает со средней долей приня-

тых (т.е. не получивших отказ) в систему заявок среди всех поступивших, поскольку заявка попавшая в очередь непременно будет обслужена.

Абсолютная пропускная способность системы

A = λQ .

Среднее число заявок Lоч , стоящих в очереди на обслуживание определяется как ма-

тематическое ожидание дискретной случайной величины k – числа заявок, стоящих в очереди:

Lоч = M (k) .

Случайная величина k принимает значения 0, 1, 2, … , m, вероятности которых определяются вероятностями состояний системы pk . Таким образом, закон распределения дискретной случайной величины k имеет следующий вид:

k			0	1		2		…	m
p	p	0	+ p	p	2	p	3	…	p m +1
		0	1		2		3

Поэтому по определению математического ожидания дискретной случайной величины (с учетом формул для вероятностей состояний) получаем:

M (k) = 0 ( p0

+ p1 ) +1 p2

+2 p3 +... +m p m +1

= ∑ jp j +1

= ∑ jρ j+1 p0 = ρ2 p0 ∑ jρ j−1 .

(19)

j=1

Предположим, что ρ ≠1. Очевидно имеем:

∑ jρ j−1 =

∑ d

ρ j

= d ∑ρ j .

j=1

dρ

j=1

Но сумма ∑ρ j

представляет собой сумму первых m членов геометрической прогрессии

j=1

ρ(1− ρ

)

ρ − ρ

m+1

ρ, ρ2 , ρ3 ,..., ρm :

∑ρ j

, ρ ≠1. Тогда

1− ρ

j=1

1− ρ

ρ − ρ

m+1

1 − ρ

(m +1−mρ)

∑

jρ j−1 =

∑

ρ j

(ρ ≠1) .

(20)

dρ

− ρ

(1− ρ)

j=1

Подставив выражение (20) в (19), найдем:

M (k) = ρ

2 p0 1− ρm (m +1−mρ) ,

(1− ρ)2

или, используя равенство

1 − ρ

(полученное при ρ ≠1), имеем

− ρ m +2

M (k) = ρ2 (1− ρm (m +1 −mρ)).

(1− ρ)(1− ρm+2 )

Если же ρ =1, то из равенства (19)

M (k) = p0 ∑ j ,

j=1

								23
а учитывая, что в этом случае p0 =	m						(сумма m членов арифме-
а учитывая, что в этом случае p0 =	1 (m +2) и ∑ j = m(m +1)						(сумма m членов арифме-
	j=1				2
тической прогрессии), окончательно получаем
M (k) = m(m +1)			(ρ =1) .
	2(m +2)
Итак, среднее число заявок в очереди
ρ2 (1− ρm (m +1−mρ))						, если		ρ ≠1;

	(1− ρ)(1− ρ		m+2	)
	(1− ρ)(1− ρ			)
Lоч =								(21)
m(m +1) ,		если			ρ =1.
	2(m +2)
	2(m +2)

Важной характеристикой СМО с ожиданием является среднее время ожидания заявки в очереди Tоч . Пусть Tоч – непрерывная случайная величина, представляющая собой время

ожидания заявки в очереди. Среднее время ожидания заявки в очереди вычислим как математическое ожидание этой случайной величины:

Tоч = M (Tоч ) .

Для вычисления математического ожидания воспользуемся формулой полного математического ожидания: если об условиях опыта можно сделать n (попарно) несовместных

гипотез H1 , H2 ,..., Hn , то полное математическое ожидание случайной величины X может быть вычислено по формуле

M ( X ) = ∑n P(Hk )M ( X | Hk ) ,

k =1

где M ( X | Hk ) – условное математическое ожидание величины X при гипотезе Hk

[Вентцель, Овчаров «Прикладные задачи теории вероятностей». – М.: Радио и связь, 1983,

с.77].

Рассмотрим m +2 несовместных гипотез Hk , k = 0,1,..., m +1, состоящих в том, что СМО находится соответственно в состояниях Sk , k = 0,1,..., m +1. Вероятности этих гипо-

тез p(Hk ) = pk , k = 0,1,..., m +1.

Если заявка поступает в СМО при гипотезе H0 , т.е. когда СМО находится в состоянии S0 , в котором канал свободен, то заявке не придется стоять в очереди и, следовательно, условное математическое ожидание M (Tоч | H0 ) случайной величины Tоч при гипотезе H0 , совпадающее со средним временем ожидания заявки в очереди при гипотезе H0 , равно нулю.

Для заявки, поступившей в СМО при гипотезе H1 , т.е. когда СМО находится в состоянии S1 , в котором канал занят, но очереди нет, условное математическое ожидание M (Tоч | H1 ) случайной величины Tоч при гипотезе H1 , совпадающее со средним временем ожидания заявки в очереди при гипотезе H1 , будет равно среднему времени обслуживания

одной заявки Tоб =1 μ .

Условное математическое ожидание M (Tоч | H2 ) случайной величины Tоч при гипотезе H2 , т.е. при условии, что заявка поступила в СМО, находящуюся в состоянии S2 , в котором канал занят и в очереди уже ждет одна заявка, равно 2μ (удвоенному среднему вре-

мени обслуживания, поскольку нужно обслужить две заявки: ту, которая находится в канале обслуживания, и ту, которая ждет в очереди). И так далее.

Если заявка поступит в систему при гипотезе Hm , т.е. когда канал занят и в очереди

ждут m −1 заявок, то M (Tоч | Hm ) = mμ .

Наконец, заявка, пришедшая в СМО при гипотезе Hm+1 , т.е. когда канал занят, m заявок стоят в очереди, и свободных мест в очереди больше нет, получает отказ и покидает систему. Поэтому в этом случае M (Tоч | H m+1 ) = 0.

Следовательно, по формуле полного математического ожидания, среднее время ожи-

дания заявки в очереди

Hk )

= ∑ pk k = 1 ∑kpk .

Tоч = M (Tоч ) = ∑ p(Hk ) M (Tоч |

m+1

k =0

k =1

μ μ k =1

Подставляя сюда выражения для вероятностей pk

( k =1,2,..., m ), получаем:

(22)

Tоч =

1 ∑kρk

= ρp0 ∑kρk −1 .

μ k =1

k =1

Если интенсивность нагрузки канала ρ ≠1,

то из равенства (22) с учетом формул

(20), (21), а также выражения для p0

находим:

1− ρ

1− ρm (m +1−mρ) =

− ρm+2

оч

(1− ρ)2

ρ2 (1− ρm (m +1−mρ)

оч

μρ(1− ρm+2 )(1− ρ)

Если же ρ =1, то, подставляя в равенство (22) выражение p0 =1 (m +2) , значение

суммы ∑k = m(m +1) 2 ,

используя формулу (21)

при

ρ =1 и учитывая,

что в данном

k =1

случае μ = λ , будем иметь

m(m +1)

Lоч

оч

2λ(m +2)

Итак, для любого ρ получаем формулу для среднего времени пребывания заявки в очереди,

которая называется формулой Литтла:

Tоч = Lλоч ,

т.е. среднее время ожидания заявки в очереди Tоч равно среднему числу заявок в очереди Lоч ,

деленному на интенсивность λ входящего потока заявок.

Пример. На автозаправочной станции (АЗС) имеется одна колонка. Площадка при станции, на которой машины ожидают заправку, может вместить не более трех машин одновременно, и если она занята, то очередная машина, прибывшая к станции, в очередь не становится, а проезжает на соседнюю АЗС. В среднем машины прибывают на станцию каждые 2 мин. Процесс заправки одной машины продолжается в среднем 2,5 мин. Определить основные характеристики системы.

Решение. Математической моделью данной АЗС является одноканальная СМО с ожиданием и ограничением на длину очереди ( m =3 ). Предполагается, что поток машин, подъезжающих к АЗС для заправки, и поток обслуживаний – простейшие.

Поскольку машины прибывают в среднем через каждые 2 мин, то интенсивность входящего потока равна λ =12 = 0,5 (машин в минуту). Среднее время обслуживания одной

							25

машины Tоб = 2,5 мин,		следовательно,		интенсивность потока			обслуживаний
μ =1 2,5 = 0,4 (машины в минуту).
Определяем интенсивность нагрузки канала: ρ = λ μ = 0,5 0,4 =1,25 .
Вычисляем вероятность		отказа P =		ρ4 (1 − ρ)		≈ 0,297 , откуда	относительная
Вычисляем вероятность		отказа P =				≈ 0,297 , откуда	относительная
			отк	1 − ρ5
			отк
пропускная способность Q =1− Pотк ≈1−0,297 = 0,703 и абсолютная пропускная способ-
ность A = λQ ≈ 0,5 0,703 ≈ 0,352 .
Среднее число машин, ожидающих в очереди на заправку
	L	=	ρ2 (1− ρ3 (4 −3ρ))		≈1,559 .
	L	=			≈1,559 .
	оч		(1− ρ)(1− ρ5 )
			(1− ρ)(1− ρ5 )

Среднее время ожидания машины в очереди находим по формуле Литтла

Tоч = Lоч λ ≈1,559 0,5 = 3,118 .

Таким образом, из анализа работы СМО следует, что из каждых 100 подъезжающих машин 30 получают отказ ( Pотк ≈ 29,7% ), т.е. обслуживаются 2/3 заявок. Поэтому необхо-

димо либо сократить время обслуживания одной машины (увеличить интенсивность потока обслуживаний), либо увеличить число колонок, либо увеличить площадку для ожидания. Оптимальное решение принимается с учетом затрат, связанных соответственно с увеличением штата обслуживающего персонала (увеличение производительности канала), с расширением площадки для ожидания или приобретением дополнительной колонки, и потерь, связанных с потерей заявок на обслуживание.

2. Одноканальная СМО с (неограниченным) ожиданием. Проанализируем работу одноканальной СМО с ожиданием без ограничений на длину очереди и на время ожидания в очереди. По-прежнему будем предполагать, что входящий поток и поток обслуживаний являются простейшими и имеют интенсивности λ и μ соответственно.

Такая система представляет собой предельный случай системы, рассмотренной в предыдущем пункте, при m →∞. Таким образом, длина очереди станет бесконечной и в соот-

ветствии с этим бесконечным станет число состояний СМО. Размеченный граф состояний представлен на рис. 11.

	λ		λ		λ
S0		S1		S2


	μ		μ			μ

...

λλ

μ μ

...

Рисунок 11.

Если отказаться от ограничения на длину очереди, то случаи ρ <1 и ρ ≥1 начинают

существенно различаться.

Если λ > μ ( ρ >1), т.е. среднее число заявок, поступивших в систему за единицу

времени, больше среднего числа обслуживаемых заявок за то же время при непрерывно работающем канале, то очевидно, что очередь неограниченно растет. В этом случае предельный режим не устанавливается и предельных вероятностей состояний не существует (точнее, они равны нулю).

В случае λ = μ ( ρ =1) только при условии, что входящий поток заявок и поток об-

служиваний регулярные (т.е. заявки поступают в СМО через равные интервалы времени, и время обслуживания одной заявки является постоянным, равным интервалу времени между поступлениями заявок), очереди вообще не будет и канал будет обслуживать заявки непрерывно. Но как только входящий поток или поток обслуживаний перестает быть регулярным и приобретает элементы случайности, очередь начинает расти до бесконечности.

Поэтому далее при рассмотрении указанных систем будем предполагать, что λ < μ, т.е. ρ <1. При этом условии с течением времени устанавливается предельный режим, и пре-

дельные вероятности состояний существуют.

Устремляя m к бесконечности в формулах для вероятностей состояний (полученных для СМО с ограниченной длиной очереди при ρ <1), находим выражения для предельных вероятностей состояний рассматриваемой СМО:

pk = lim ρk p0		= ρk lim	1− ρ	= ρk	(1− ρ) ; k = 0,1,2,..					(23)
pk = lim ρk p0		= ρk lim	m+2	= ρk	(1− ρ) ; k = 0,1,2,..					(23)
m →∞		m →∞	1− ρ
Предельные вероятности (23) удовлетворяют нормировочному условию
В самом деле,		p0 + p1 + p2 +... =1.
В самом деле,
	∞	∞			∞
	∑ pk = ∑ρk (1− ρ) = (1−				ρ)∑ρk .
	k =0	k =0			k =0
∞
Но ряд ∑ρk представляет собой сумму бесконечно убывающей геометрической прогрес-
k =0
сии с первым членом b = ρ0 =1 и знаменателем ρ <1. Поэтому
1	1						1
∞				∞
∑ρk =		и, следовательно, ∑ pk			= (1− ρ)				=1.
∑ρk =	1− ρ	и, следовательно, ∑ pk			= (1− ρ)	1	−	ρ	=1.
k =0	1− ρ		k =0			1	−	ρ

При отсутствии ограничений на очередь каждая заявка, поступившая в СМО, рано или поздно будет обслужена. Поэтому вероятность отказа равна нулю: Pотк = 0 .

Следовательно, вероятность того, что поступившая заявка будет принята в систему, так же как и относительная пропускная способность Q , равна единице:

Q =1− Pотк

=1.

Тогда для абсолютной пропускной способности

A (и интенсивности выходящего потока)

будем иметь: A = λQ = λ, т.е. интенсивности входящего и выходящего потоков совпадают.

Среднее число заявок в очереди Lоч

получим из формулы (21) при ρ <1 переходом к

пределу при m →∞:

(1− ρm (m +1−mρ))

ρ2 (1−mρm (1+1 m − ρ))

Lоч = lim

ρ2

= lim

(1− ρ)(1− ρ

m+2

)

1− ρ

m →∞

Известно, что бесконечно малая ρm ( ρ <1, m →∞) является бесконечно малой бо-

лее высокого порядка,

чем бесконечно

малая

m−1

( ρm = o(m−1 ) ), т.е. mρm →0 при

m →∞. Следовательно, L

ρ2

− ρ

оч

Среднее время ожидания заявки в очереди по формуле Литтла равно

ρ2

оч

λ(1

− ρ)

μρ

(1−

ρ)

μ(1−

ρ)

оч

Наконец, среднее время пребывания заявки в СМО T

СМО

складывается из среднего

времени заявки в очереди Tоч

и среднего времени обслуживания заявки Tоб :

TСМО =Tоч +Tоб = μ(1ρ− ρ) + μ1 = μ(11− ρ) = λ(1ρ− ρ) .

Пример. В парикмахерской работает только один мужской мастер. Среднее время стрижки одного клиента составляет 20 мин. Клиенты в среднем приходят каждые 25 мин. Средняя стоимость стрижки составляет 60 руб. Как в первую смену с 9 до 15, так и во вторую – с 15 до 21, работают по одному мастеру. Провести анализ работы системы обслуживания. Определить ежедневный «чистый» доход каждого мастера, если он получает только 30% от выручки (остальное уходит на оплату аренды помещения, налоги, амортизацию оборудования и проч.).

Решение. Интенсивность входящего потока λ = 2,4 клиента/ч, интенсивность потока обслуживаний μ =1 Tоб =1 20 мин = (1/13)ч =3 клиента/ч. Находим:

интенсивность нагрузки (канала) мастера ρ = λμ = 0,8 ;

долю времени (вероятность) простоя мастера p0

=1− ρ =1−0,8 = 0,2 ;

вероятность того, что мастер занят работой pзан

=1− p0

=1−0,2 = 0,8 ;

среднее число клиентов в очереди L

ρ2

0,82

=3,2 клиента;

− ρ

1 −0,2

оч

Lоч

3,2

=1,34 мин;

среднее время ожидания в очереди T

2,4

оч

среднее время пребывания клиентов в парикмахерской

=1,34 + 20 = 21,34 мин.

СМО =Tоч +Tоб

Система работает вполне удовлетворительно. Поскольку ρ <1, то режим работы сис-

темы устойчивый, 20% рабочего времени мастер не занят, а остальные 80% времени занят работой, длина очереди 3,2 клиента небольшая, а среднее время пребывания клиента в парикмахерской всего 21,34 мин.

Каждый мастер занимается обслуживанием клиентов в среднем ежедневно в течение

0,8 (15 −9) = 4,8 ч = 288 мин.

За это время он обслужит 28820 =14,4 клиента, поэтому ежедневная выручка в среднем

составит 14,4 60 =864 руб. Ежедневный «чистый» доход каждого мастера в среднем составляет 864 0,3 = 259,2 руб.

<<< < Предыдущая 1 23 / 33

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.02.2015707.38 Кб61Хмылев Организация работы отдела.pdf
#
22.09.2019184.21 Кб1Хор.Шпора.rtf
#
22.09.2019147.72 Кб1Хор.Шпора2.rtf
#
13.02.20154.23 Mб15хорошев 5 раз.docx
#
13.02.2015385.02 Кб13ХОРОШИЕ - Лекции по философии.doc
#
13.02.2015695.43 Кб11Хорошие лекции.pdf
#
22.08.2019291.33 Кб3христианство и труд.doc
#
15.11.2019122.37 Кб13Христианство.doc
#
15.11.201913.57 Mб8Хроленко-2.doc
#
13.02.2015114.18 Кб4Хроника литературной жизни.doc
#
13.02.20151.23 Mб11Хроники Акаши.rtf