
- •Содержание
- •3 Расчет и конструирование колонны
- •3.1 Определение расчетной длины надкрановой и подкрановой частей колонны в плоскости и из плоскости рамы
- •Подбор сечения стержня колонны и проверка общей и местной устойчивости.
- •Расчет надкрановой части колонны
- •Подкрановая ветвь
- •3.2.2.2 Наружная ветвь
- •3.2.3.1 Подкрановая ветвь.
- •Проверка устойчивости подкрановой части колонны как единого составного стержня в плоскости действия изгибающего момента
Подкрановая ветвь
Принимаем
подкрановую ветвь в виде сварного
двутавра. Предварительно назначаем
коэффициент продольного изгиба
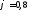 .
.
Требуемая площадь сечения составит:

Компонуем сечение, исходя из требуемой площади. Ширина двутавра должна удовлетворять условию:
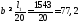 см.
см.
Принимаем
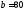 см.
см.
Ширина полок двутавра будет равна:
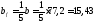 см.
см.
Принимаем
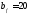 см.
см.
Принимаем:
толщина стенки
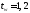 см,
толщина полок
см,
толщина полок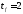 см.
см.
Высота
стенки при этом составит:
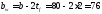 см.
см.
Фактическая площадь сечения при этом составит:
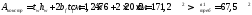 .
.
Вычисляем геометрические характеристики подобранного сечения:
Момент инерции сечения относительно оси X:
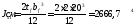 ;
;
Момент инерции сечения относительно оси Y:
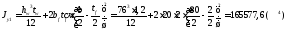
Радиусы инерции по осям XиY:
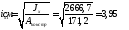 ;
;
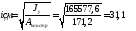 ;
;
3.2.2.2 Наружная ветвь
Предварительно назначаем коэффициент
продольного изгиба
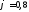 .
.
Требуемая площадь сечения составит:
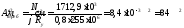
Ширина листа принимается равной:
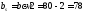 .
.
Толщину листа принимаем равной
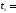 20мм.
20мм.
Площадь, приходящаяся на пластину составит
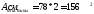
Что значительно больше Атр, поэтому
конструктивно принимаем уголок ∟75×5
по ГОСТ 8509-93 с площадью сечения
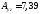 см2.
см2.
С учетом этого площадь сечения составит:
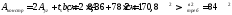 .
.
Определяем координаты центра тяжести наружной ветви относительно наружной грани листа.
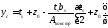 ,
где
,
где
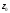 - расстояние от центра тяжести уголка
до его грани. Для уголка ∟75×5 расстояние
- расстояние от центра тяжести уголка
до его грани. Для уголка ∟75×5 расстояние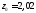 см.
см.
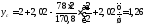 см;
см;
Вычисляем геометрические характеристики подобранного сечения:
Момент инерции сечения относительно оси X:
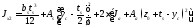
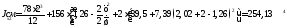 ;
;
Момент инерции сечения относительно оси Y:
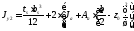 ;
;
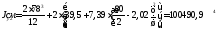 .
.
Радиусы инерции по осям XиY:
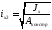
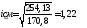
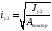

Определяем координаты центра тяжести всего сечения относительно центральной оси:
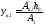 ,
где
,
где
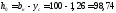 см;
см;
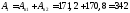 см2;
см2;
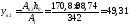 см;
см;
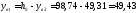 см.
см.
Вычисляем геометрические характеристики всего сечения:
Момент инерции сечения относительно оси X:
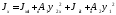
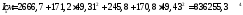
Радиус инерции по оси X:
 .
.
3.2.3 Проверка устойчивости отдельных ветвей колонны
3.2.3.1 Подкрановая ветвь.
Определяем уточненное продольное усилие в подкрановой ветви с учетом координат центра тяжести:
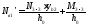
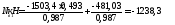
Гибкость в плоскости рамы
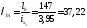
Расстояние между узлами решетки принято из следующего расчета:
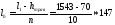 см.
см.
Гибкость из плоскости рамы
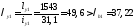 ;
;
Максимальная условная гибкость
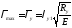 ,
,
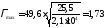
Коэффициент продольного изгиба
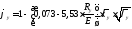 ;
;
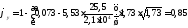 .
.
Напряжение:
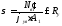 ;
;
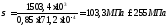 -
условие соблюдается, устойчивость
подкрановой ветви колонны из плоскости
рамы обеспечена.
-
условие соблюдается, устойчивость
подкрановой ветви колонны из плоскости
рамы обеспечена.
3.2.3.2 Наружная ветвь.
Определяем уточненное продольное усилие в наружной ветви с учетом координат центра тяжести:
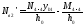
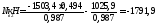
Гибкость в плоскости рамы
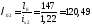
Расстояние между узлами решетки принято из следующего расчета:
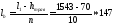 см.
см.
Гибкость из плоскости рамы

Максимальная условная гибкость
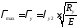 ,
,
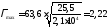
Коэффициент продольного изгиба
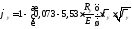 ;
;
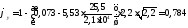
Напряжение:
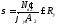 ;
;
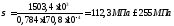 -
условие соблюдается, устойчивость
подкрановой ветви колонны из плоскости
рамы обеспечена.
-
условие соблюдается, устойчивость
подкрановой ветви колонны из плоскости
рамы обеспечена.
Расчет элементов соединительной решетки подкрановой части колонны.
Соединительную
решетку выполняем из уголков. Расчет
решетки производим на поперечную силу
в сечении 4-4 колонны:
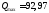 кН.
кН.
Угол между осями ветвей и раскосов:
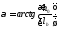
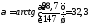 º
º
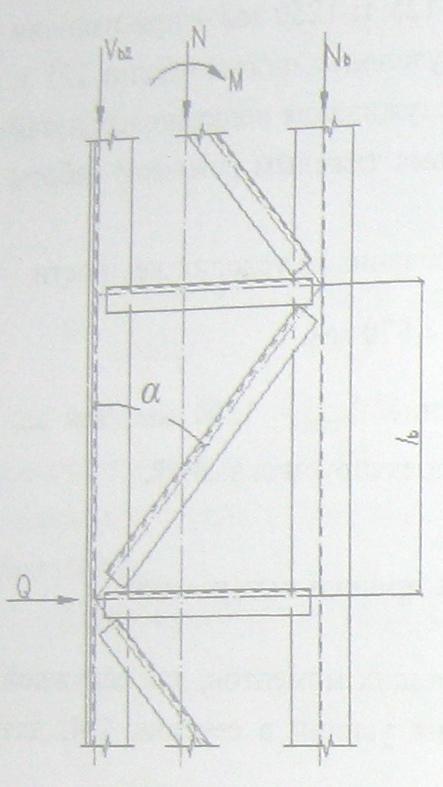
Рисунок 14 - Схема соединительной решетки
Отсюда
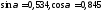 .
.
Усилие в раскосе при наличии решетки в двух плоскостях:
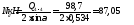 ;
;
Геометрическая длина раскоса при центрировании на ось ветви:
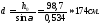
Задаваясь
коэффициентом продольного изгиба
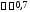 ,
находим требуемую площадь сечения
сжатого раскоса:
,
находим требуемую площадь сечения
сжатого раскоса:
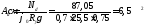 ,
,
Принимаем
раскосы из уголков: ∟125 9
9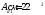 с радиусом инерции 2,48 см.
с радиусом инерции 2,48 см.
Гибкость раскоса при шарнирном закреплении в узлах
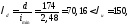
Условная гибкость
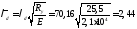 .
.
Следовательно, коэффициент продольного изгиба вычисляем по формуле
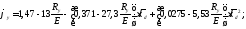
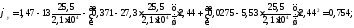
Отсюда напряжение
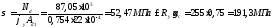 ,
,
Усилие в распорках незначительно, поэтому распорки выполняем из тех же уголков, что и раскосы.
