
1.3 Задача № 14
Рассчитать открытую зубчатую цилиндрическую прямозубую передачу: определить модуль; основные размеры цилиндрических прямозубых колёс; силы, действующие на валы; проверить рассчитанную передачу на прочность по напряжениям изгиба (рисунок 5).
Мощность
на ведущем валу
 ,
угловая скорость ведомого вала
,
угловая скорость ведомого вала
 ,
передаточное число u
(передача нереверсивная, нагрузка
постоянная). Исходные данные приведены
в таблице 3.
,
передаточное число u
(передача нереверсивная, нагрузка
постоянная). Исходные данные приведены
в таблице 3.
Рисунок 5 – Схема открытой цилиндрической прямозубой передачи
Таблица 3 - Исходные данные
|
Показатель |
|
|
u |
Материал шестерни |
Материал колеса |
Термообработка |
|
Значение |
8 |
3,6 |
3,15 |
Сталь 35 ХM |
Сталь 40Х |
Улучшение |
Решение:
1)
Определяю угловую скорость шестерни
 ,
если передаточное число u
равно:
,
если передаточное число u
равно:
u
=
 =
=
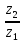 =
=
 ;
(23)
;
(23)
 =
u
∙
=
u
∙
 = 3,15 ∙3,6 = 11,3 рад/с.
= 3,15 ∙3,6 = 11,3 рад/с.
2) Задаю число зубьев шестерни (из рекомендованного количества
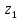 =
17…24):
=
17…24):
 =
20
=
20
и
определяю число зубьев колеса
 из выражения (23):
из выражения (23):
 =
u
∙
=
u
∙
 = 3,15 ∙ 20 = 63.
= 3,15 ∙ 20 = 63.
3)
Определяю вращающий момент
 на
валу шестерни, Н ∙ м:
на
валу шестерни, Н ∙ м:
 =
=
 ;
(24)
;
(24)
 =
=
 = 707 Н ∙ м.
= 707 Н ∙ м.
4)
Принимаю твёрдость (HB)
материалов зубчатых колёс согласно
заданной марке стали,
 :
:
для
шестерни
 =
255 и для колеса
=
255 и для колеса
 = 235.
= 235.
5) Рассчитываю допускаемые напряжения изгиба зубьев
шестерни и колеса, МПа:
 =
=
 ∙
∙
 ,
,
 =
=
 ∙
∙
 ,
(25)
,
(25)
где
 ,
,
 – пределы выносливости зубьев при
изгибном нагружении для шестерни и
колеса соответственно, МПа; при
термообработке нормализация
– пределы выносливости зубьев при
изгибном нагружении для шестерни и
колеса соответственно, МПа; при
термообработке нормализация
 =
1,75
=
1,75
 ,
,
 = 1,75
= 1,75
 ;
;
 =
(1,4…1,7) – коэффициент безопасности;
=
(1,4…1,7) – коэффициент безопасности; – коэффициент долговечности; для
длительно работающих передач
– коэффициент долговечности; для
длительно работающих передач
 =
=
 = 1;
= 1;
 =
=
 ∙ 1 = 297,5 МПа;
∙ 1 = 297,5 МПа;
 =
=

 1 = 274,2 МПа.
1 = 274,2 МПа.
6)
Нахожу коэффициенты формы зубьев
 и
и
 в зависимости от числа зубьев
в зависимости от числа зубьев
 и
и
 по таблице 15:
по таблице 15:
 =
4,07;
=
4,07;
 =
3,62.
=
3,62.
7) Провожу сравнительную оценку прочности зубьев шестерни и колеса на изгиб по отношениям:
 и
и
 ;
(26)
;
(26)
менее прочным является то зубчатое колесо пары, у которого это отношение больше.
 =
0,013681
=
0,013681

 = 0,013202,
= 0,013202,
следовательно, менее прочным является зубчатое колесо шестерни; все дальнейшие расчёты ведутся по менее прочному зубчатому колесу.
8)
Определяю модуль зацепления
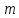 по напряжениям изгиба, мм:
по напряжениям изгиба, мм:
 =
1,4 ∙
=
1,4 ∙
 ,
(27)
,
(27)
 =
1 − коэффициент, учитывающий неравномерность
распределения нагрузки по длине зуба;
=
1 − коэффициент, учитывающий неравномерность
распределения нагрузки по длине зуба; – коэффициент зубчатого венца колёс;
– коэффициент зубчатого венца колёс;
 = 0,8 (симметричное расположение колёс
относительно опор вала);
= 0,8 (симметричное расположение колёс
относительно опор вала);
 =
1,4 ∙
=
1,4 ∙
 =4,4 мм.
=4,4 мм.
По ГОСТ 9563−60 принимаю стандартное значение m = 4,0 мм.
9) Определяю основные геометрические размеры передачи, мм:
- диаметры делительные
 =
=
 ;
;
 = m
∙
= m
∙
 ;
(28)
;
(28)
 =
4 ∙ 20 = 80 мм;
=
4 ∙ 20 = 80 мм;
 =
4 ∙ 63 = 252 мм;
=
4 ∙ 63 = 252 мм;
- диаметры вершин зубьев:
 =
=
 + 2m;
+ 2m;
 =
=
 + 2m;
(29)
+ 2m;
(29)
 =80
+ 2 ∙ 4 = 88 мм;
=80
+ 2 ∙ 4 = 88 мм;
 =
252 + 2 ∙ 4 = 260 мм;
=
252 + 2 ∙ 4 = 260 мм;
- диаметры впадин зубьев
 =
=
 − 2,5m;
− 2,5m;
 =
=
 - 2,5m;
(30)
- 2,5m;
(30)
 =
80– 2,5 ∙ 4 = 70 мм;
=
80– 2,5 ∙ 4 = 70 мм;
 =
252 – 2,5 ∙ 4 = 242 мм;
=
252 – 2,5 ∙ 4 = 242 мм;
- ширина венцов
 =
=
 ∙
∙
 ;
;
 =
=
 + (2…5);
(31)
+ (2…5);
(31)
 =
0,8 ∙ 80 = 64 мм;
=
0,8 ∙ 80 = 64 мм;
 =
64 + 3 = 67 мм;
=
64 + 3 = 67 мм;
- межосевое расстояние:
 =
=
 ;
(32)
;
(32)
 =
=
 = 166 мм.
= 166 мм.
10) Определяю силы в зацеплении, Н (рисунок 6):
- окружные:
 =
=
 =
=
 ;
(33)
;
(33)
 =
=
 = 17675 Н;
= 17675 Н;
- радиальные:
 =
=
 =
=
 ∙
∙
 ,
(34)
,
(34)
где
 = 20
= 20
 =
17675 ∙ tg
20
=
17675 ∙ tg
20 =
6433 Н.
=
6433 Н.
Рисунок 6 – Схема сил в зацеплении передачи
11) Проверяю рассчитанную передачу по направлениям изгиба, МПа:
 =
=


 ,
(35)
,
(35)
где
 − коэффициент, учитывающий неравномерность
распределения нагрузки между зубьями;
для прямозубых колёс
− коэффициент, учитывающий неравномерность
распределения нагрузки между зубьями;
для прямозубых колёс
 = 1;
= 1;
 – коэффициент динамической нагрузки,
зависящий от степени точности и окружной
скорости.
– коэффициент динамической нагрузки,
зависящий от степени точности и окружной
скорости.
Степень
точности назначается в зависимости от
окружной скорости
 :
:
 =
=

 , м/с,
(36)
, м/с,
(36)
где
 −
угловая скорость, рад/с;
−
угловая скорость, рад/с;
 – диаметр делительный, м;
– диаметр делительный, м;
 11,3
11,3
 = 0,5 м/с,
= 0,5 м/с,
тогда
 = 1,06 при степени точности, равной 6
(таблица 16).
= 1,06 при степени точности, равной 6
(таблица 16).
Следовательно,
 =
=
 =
297,9 МПа;
=
297,9 МПа;
12)
 Расчётное
напряжение изгиба
Расчётное
напряжение изгиба меньше допускаемого
меньше допускаемого
 на 29,0 МПа, следовательно, перегрузка
передачи на %, что недопустимо.
на 29,0 МПа, следовательно, перегрузка
передачи на %, что недопустимо.
Уменьшаю
ширину венца колеса
 до 41 мм, тогда
до 41 мм, тогда
 =
=
 = 298,5 МПа.
= 298,5 МПа.
Расчётное напряжение изгиба больше допускаемого на 1,0 МПа, что составляет % перегрузки передачи.

 ,
кВт
,
кВт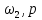 ад/с
ад/с