5.2. Варианты задач и примеры их решения Задача д-4. Теорема о движении центра масс

а) Исходные данные.Расчетная схема (общая для всех вариантов задач) приведена на рис.4.1, исходные данные – в табл.4.1.

Таблица 4.1.

Рис.4.1. Примечание. Функцию выбирают по последней цифре шифра, угол- по предпоследней	Цифра шифра	Функция , м	Угол , град
	0		30
	1		45
	2		60
	3	­	75
	4		60
	5		75
	6		45
	7		30
	8		45
	9		150

б) Условие задачи

Дано:материальная система, состоящая из двух тел. Тело 1 представляет собой плиту, расположенную вертикально и перемещающуюся в двух направляющих со скоростьюм/с в плоскости чертежа, Масса плитыкг.

Тело 2 представляет собой материальную точку Dмассойкг. Она перемещается по желобуAB. Закон ее движения имеет вид. Угол наклона желоба к горизонтальной оси. Выражение дляSи значение углаприведены в табл.4.1.

В начальный момент времени .

Составить уравнения движения центра масс (точки С) материальной системы и определить значения ,иNв момент временис.

в) Указания по решению задач

1. Для решения задачи Д-4 надо применить дифференциальные уравнения движения центра масс. Так как и, то получим

; (а)

. (б)

2. Из уравнения (а) найдем закон движения центра масс.

Последовательно интегрируя, получим

; (в)

, (г)

где и- постоянные интегрирования, которые находим из начальных условий:;.

Из уравнений (б) найдем нормальную реакцию N.

3. Координаты центра масс материальной системы находят по формулам.

; (д)

. (е)

Здесь обозначены:

,M– массы тел 1 и 2 по отдельности и масса всей материальной системы:;

- координаты центров масс тел 1 и 2. Их находим по следующим формулам:

Таким образом, имеем

;

.

Взяв производные, получим выражение для скорости центра масс в проекции xиy:

;

.

Следовательно

то есть

4. Из уравнения (в) следует, что скорость движения центра масс вдоль оси xявляется постоянной (третье следствие к теореме: если, тоявляется постоянной).

При с имеем

.

5. Значение Nнаходим из уравнения (б)

,

Так как

,

то

,

следовательно

.

Задача решена полностью.

г) Пример решения задачи.

Расчетная схема приведена на рис.4.2.

Дано:кг,кг,м/с,,.

Определить: для момента времени с значения:,,.

Решение:а) рассмотрим движение материальной системы вдоль оси.

Н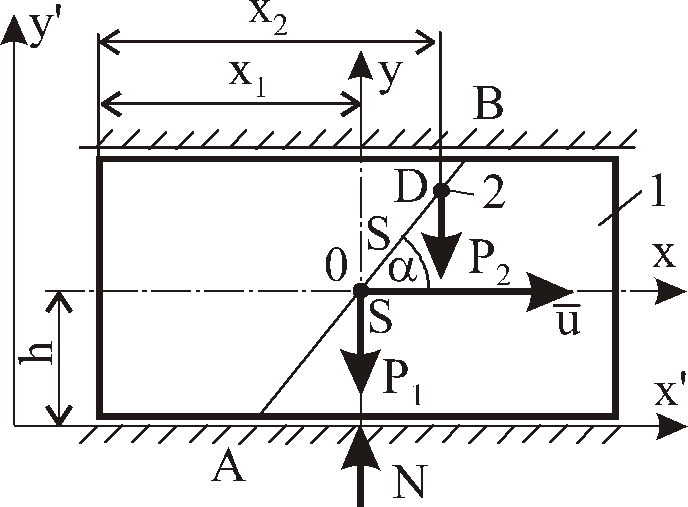аходим для момента временизначенияи:

Т

Рис.4.2.

ак каки, то,.

Следовательно

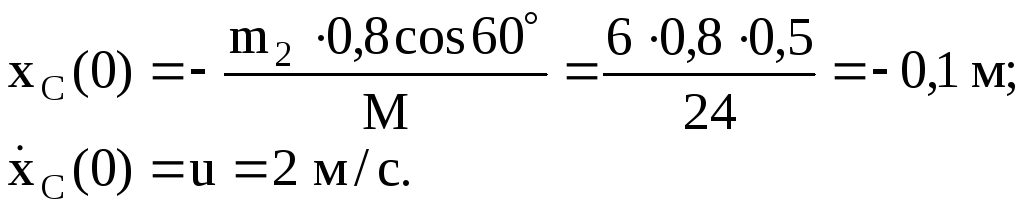
Таким образом м/с,м/с и уравнение движения центра масс имеет вид

,

отсюда

м/с.

При с имеем:м;м/с.

б) найдем значения по формуле

.

Здесь

и

.

Находим вторую производную от S:

и ее значение при с

м/с.

Значит

Н.

Таким образом, задача решена.

Задача д-5. Теорема об изменении кинетического момента материальной системы (теорема моментов)

а) Исходные данные.Расчетная схема (общая для всех вариантов задач) приведена на рис.5.1, исходные данные – в табл.5.1.

Таблица 5.1.

Рис.5.1. Примечание. Функцию выбирают по последней цифре шифра, момент М - по предпоследней	Цифра шифра	Функция , м	Положение точки А	Направле­ние отсчета S	М, Нм
	0		1	По ходу вращения	0
	1		2	-"-	12
	2		3	-"-	-5
	3		4	Против хода	0
	4		1	-"-	8
	5		2	-"-	-10
	6		3	-"-	0
	7		4	-"-	20
	8		1	По ходу вращения	-15
	9		2	-"-	0

б) Условие задачи

Дано:материальная система, состоящая из двух тел. Тело 1 представляет собой диск радиусомм и массойкг. Он вращается вокруг неподвижной вертикальной осиzс начальной угловой скоростью. Тело 2 представляет собой материальную точкуDмассойкг, которая движется по круглому желобу (пунктир по поверхности диска) радиусомм. Закон движения точки. Начало отсчета величиныSпоказано для отдельных вариантов задач цифрами 1, 2, 3, 4 на диске. Направление отсчета – по ходу и против хода часовой стрелки, как показано в табл.5.1 с помощью знака момента.

После начала вращения диска на него действует пара сил с моментом М, лежащим в плоскости диска. Если , то ее момент направлен по направлению вращения диска, если- в обратную сторону.

Определить: угловую скорость вращения диска в конце движения дляс.

в) Указания к решению

1. Задачу Д-5 решают с помощью теоремы моментов. Расчетное уравнение имеет вид

.

2. Величина - кинетический момент материальной системы.вданной задаче он равен сумме кинетических моментов двух тел

.

Кинетический момент диска вычисляют по формуле

,

где - момент инерции диска относительно оси вращенияz. Для сплошного круглого диска.

Точка Dсовершает сложное движение: переносное вместе с диском и относительное – по диску, значит

,

где (- момент количества движения точки относительно оси вращения);

(- количество движения точки в относительном движение по диску).

Таким образом,

.

При вращении тела и движении точки в одну сторону записывают знак "+", в разные – знак "-".

3. Величина - сумма моментов внешних сил относительно осиz. Так силы тяжести ипараллельны осиZ, то их моменты равны нулю. Значит

.

4. Таким образом, расчетное уравнение принимает вид

.

Отсюда () имеем

или

.

5. Постоянную интегрирования находим из нулевых начальных условиях: при,,.

Следовательно

.

Значит

.

Отсюда выражаем прис.

г) Пример решения задачи.

Расчетная схема приведена на рис.5.2.

Дано: м,м,;кг;кг;,движение точки D направлено против часовой стрелки, вращение по часовой стрелке, то естьНм.

О

Рис.5.2.

пределить:прис.

Решение:

1. Запишем расчетное уравнение в общем виде

.

Отсюда имеем (при )

. (1)

2. Запишем выражение для

.

Здесь .

Значит

.

Тогда

. (2)

3. Вычислим значение . При, значит

,

где .

Подставим теперь выражения (2) и в уравнение (1)

. (3)

Выражаем теперь значение прис:

.

Отсюда имеем

.

Таким образом, задача решена.