Ответ: |
|
|
|
Xa 1.732 |
Ya 5 |
ma 9.464 |
|
Знаки в ответах свидетельствуют о том, что реакция X A |
на |
||
схеме, рис. 14, показана противоположно действительному |
|||
направлению, направления YA и mA показаны верно. |
|
||
Для проверки результатов решения составили уравнение: |
|
||
|
n |
r |
|
mC Fk 0.
k 1
ma Q BE m Ya AB Xa BC 0 
Уравнение тождественно удовлетворится. Следовательно, в решении нет ошибок.
54
В результате решения уравнений получили:
ХА= – 1,73 кН; YА = 5,00 кН; mА = 9,46 кНм.
55
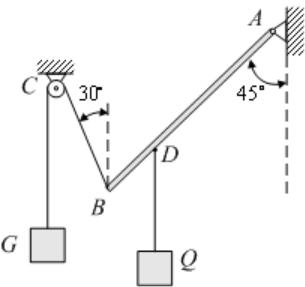
4.Задачи для самостоятельного решения
1.Однородная балка АВ весом Р = 100 Н прикреплена к стене шарниром А и удерживается под углом 45o к вертикали при помощи троса, перекинутого через блок С и несущего груз G. Ветвь ВС троса образует с вертикалью угол 30o. В точке D к балке подвешен груз Q весом 200 Н, рис. 15. Определить вес груза G и реакцию шарнира А, пренебрегая трением на блоке, если ВD =BA/4.
Ответ: G = 146,38 H; XA = 73,19 H;
YA = 173,24 H.
Рис. 15 |
56 |
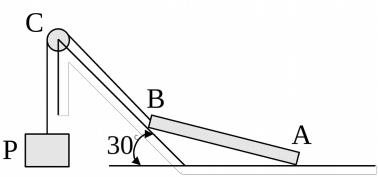
2. Однородный стержень АВ весом 100 Н опирается одним концом на гладкий горизонтальный пол, другим – на гладкую плоскость, наклонённую под углом 30 к горизонту. У конца В стержень поддерживается верёвкой, перекинутой через блок С и несущей груз Р, часть верёвки ВС параллельна наклонной плос- кости, рис. 16.
Пренебрегая трением на блоке, определить величину груза Р и силы давления NА и NВ на пол и на наклонную плоскость.
Ответ: P = 25 H;
NA = 50 H;
NB = 43,3 H.
Рис. 16
57
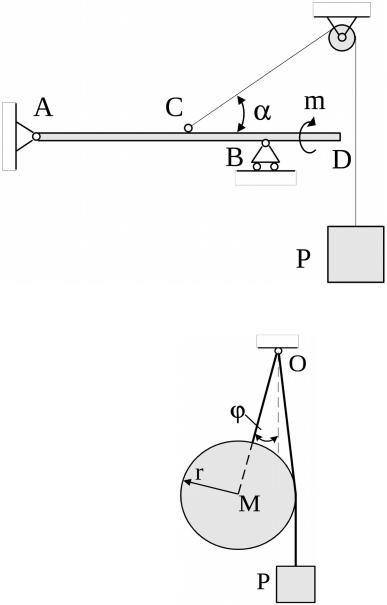
3. Определить реакции опор А и В невесомой балки, изобра- жённой на рис. 17, приняв при расчёте АС = CD = 1 м; СВ = ВD; Р
= 2 кН; m = 3 кНм; = 30 . |
|
Ответ: |
|
XA = -1,73 кH; YA = -2,33 кH. RB = 1,33 кH. |
Рис. 17 |
4. Однородный шар весом Q и радиусом r и |
|
гиря весом Р подвешены на верёвках в точке |
|
О, как показано на рис. 18. Расстояние ОМ = |
|
b. |
|
Определить, какой угол образует прямая |
|
ОМ с вертикалью при равновесии. |
|
Ответ: sin = aP/b(P+Q) |
Рис. 18 58 |
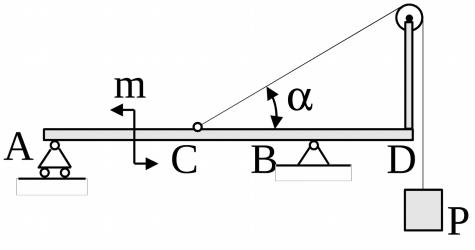
5. Определить реакции опор А и В невесомой балки, изображённой на рис. 19, приняв при расчёте АС = CD = 1 м; СВ = BD; Р = 2 кН; m = 3 кНм; = 30 . Размерами блока пренебречь.
Рис. 19
Ответ: XB =0; YB = 0,67 кH. RA = 1,33 кH.
59
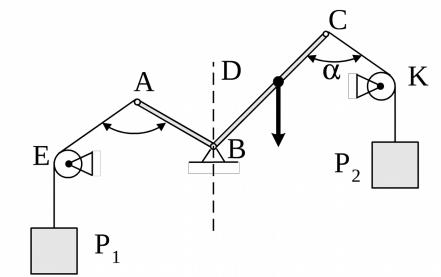
6. Ломаный рычаг АВС, имеющий неподвижную ось В, весом P = 80 Н; плечо АВ = 0,4 м, плечо ВС = 1 м, центр тяжести рычага находится на расстоянии 0,212 м от вертикаль- ной прямой ВD. В точках А и С привязаны верёвки, перекинутые через блоки Е и К и натягиваемые гирями весом Р1 = 310 Н и Р2 = 100 Н, рис. 20.
Пренебрегая трением на блоках, определить угол ВСК = в положении равновесия, если угол ВАЕ = 135 .
Ответ: =45o; = 135o. |
Рис. 20 |
|
|
||
1 |
2 |
60 |
|
|
|
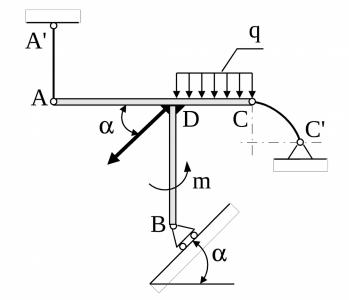
7. Определить реакции опор балки, изображённой на рис. 21, если известны: F = 500 Н, q = 200 Н/м, = 30 ; АА и СС – жёсткие невесомые стержни; АD = BD = CD = 0,5 м; m = 750 Нм.
Рис. 21
Ответ: RA =647,94 H; RB = 369,05 H. RC = 873,34 H.
61
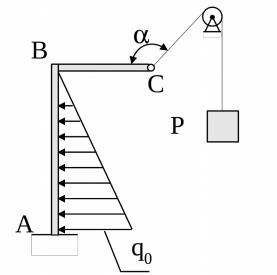
8. Для балки АВС, изображённой на рис. 22, определить реакции жёсткой заделки, если известны: АВ = 4,5 м, ВС = 1,5 м, = 120 ; Р = 25 кН; q0 = 24 кН/м; АВ ВС.
Рис. 22
Ответ: XA = 2,00 кH; YA = -4,33 кH. MA = -2,00 Hм.
62
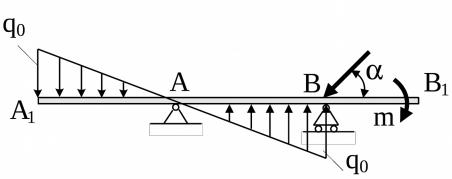
9. Определить реакции опор А и В двухконсольной балки, находящейся под действием сосредоточенной силы Р, пары сил с моментом m и распределённой нагрузки, изменяющейся по закону треугольника, рис. 23. В расчёте принять: Р = 2 кН, m = 3 кНм, q0 = 3 кН/м: А1А = АВ = ВВ1 = 0,6 м; = 60 .
Рис. 23
Ответ: XA = 1,00 кH; YA = 2,60 кH. RB = 4,33 кH.
63