kontra_po_tfkp_za_03-04_gg_s_resheniami / z6_v31

3

Вычисление интеграла по вещественной оси с помощью вычетов

2003/2004 31

6	Пусть - регулярная ветвь многозначной функции в плоскости с разрезом по кривой такая, что . Пусть . Найти и вычислить интеграл .

  Шабунин, Сидоров стр. 81 – 119 (пример 9 стр. 110-111, пример 12 стр. 103-115), Половинкин_н стр. 108 – 115 (пример 4 стр. 114 – 115)

 Прежде всего следует проверить, что в заданной области действительно существуют регулярные ветви функции ¹. Эта функция допускает выделение регулярных ветвей в области G=C\, что легко проверяется².

 Выберем теперь регулярную ветвь корня, которая удовлетворяет условию :

= = = 1 = , т.е. .

- (1)

регулярная ветвь, соответствующая вышеприведенному условию .

 Для вычисления вычета функции f(z)в точке ( - УОТ³) разложим эту функцию в ряд Лорана в кольце . Для этого воспользуемся разложением f(z) в точке вещественной оси: = = = = = = .

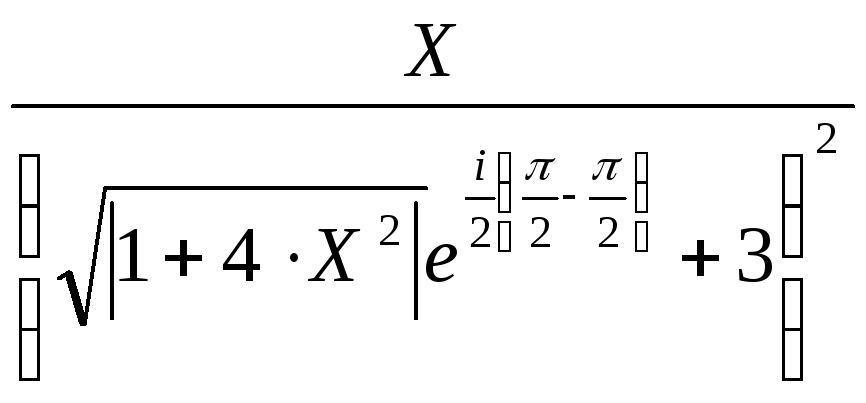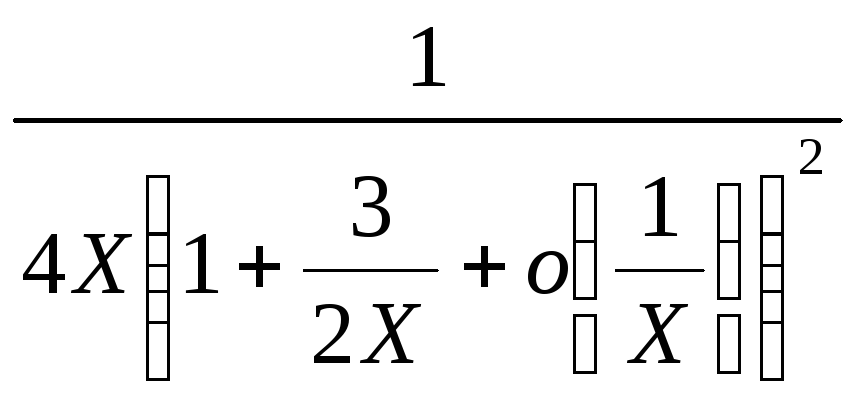По теореме единственности⁴ имеем: . Откуда получаем, что коэффициент при равен , следовательно ⁵.

 Находим особые точки .

Особыми точками являются: ,

особые точки числителя: ,

нули знаменателя: ,

      :

 , = = 3 – не подходит,

 , = = =

особые точки знаменателя: .

Вне контура находятся: - УОТ,

- П² (полюс 2-го порядка)⁶:

  =  ,

=  = = = =

= = = 0,

= = = =

 Интеграл 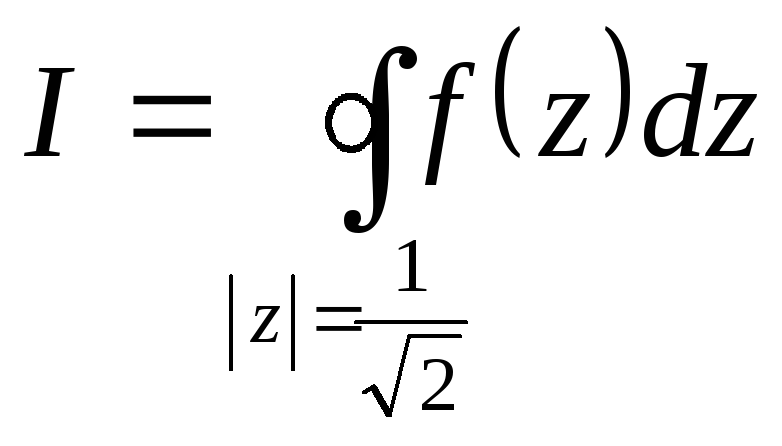, можно вычислить по формуле ⁷.

 Точка - П² (полюс 2-го порядка), поэтому вычет⁸ в этой точке равен . 

Кроме того, ⁹, где - коэффициент разложения функции в ряд Лорана с центром в конечной точке при .

Рассмотрим точку . = = = = = = = = = = = = = =

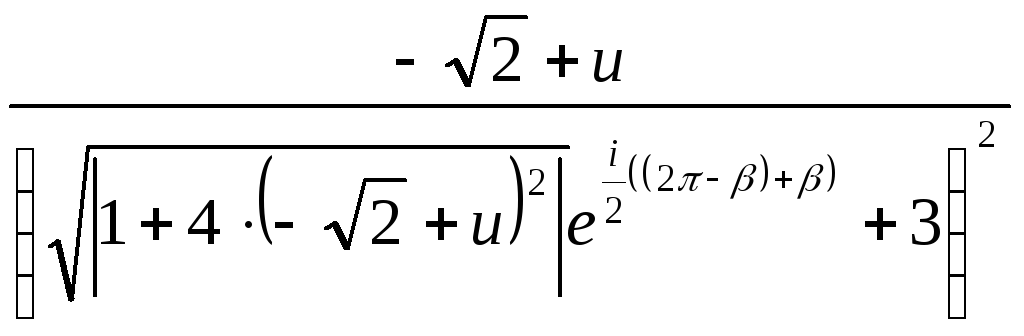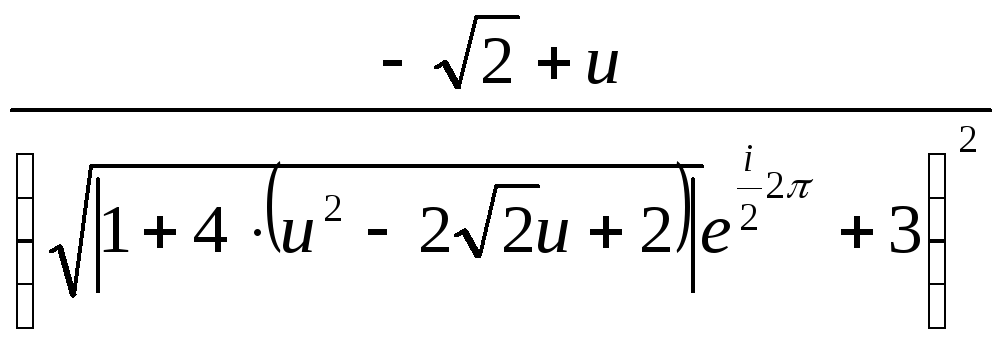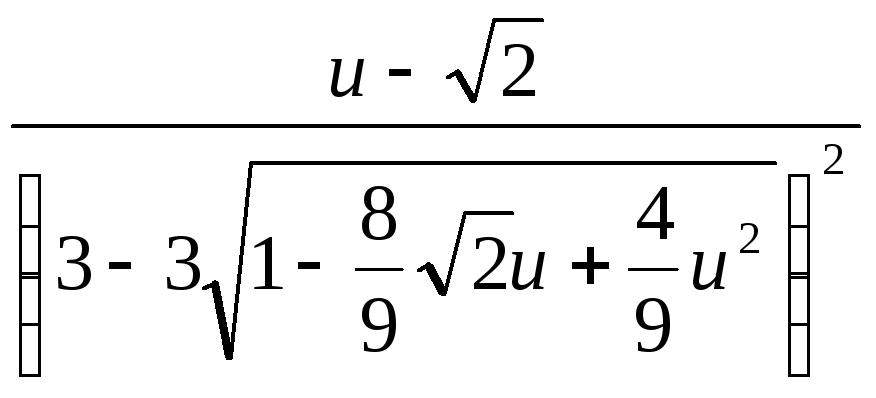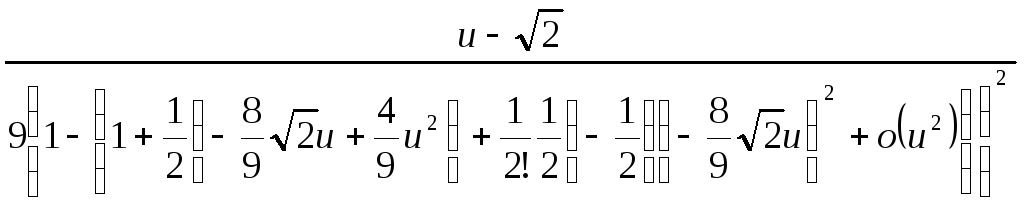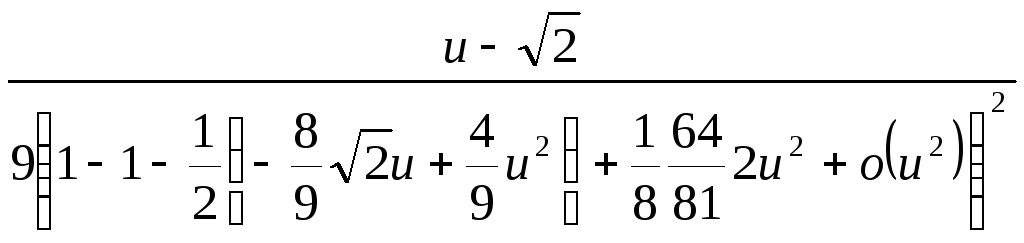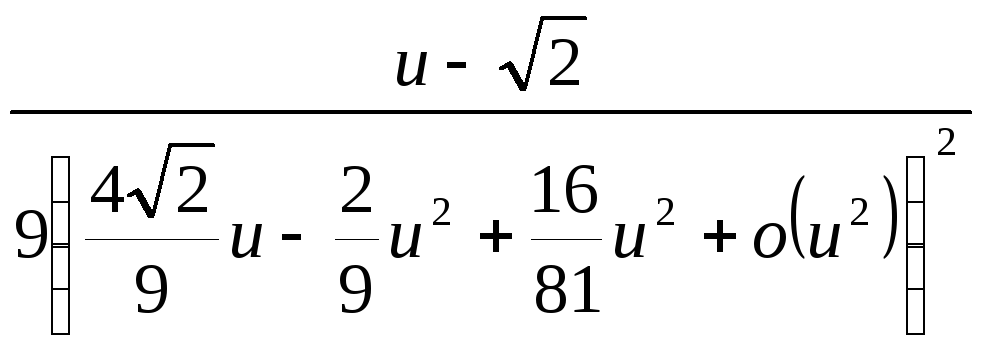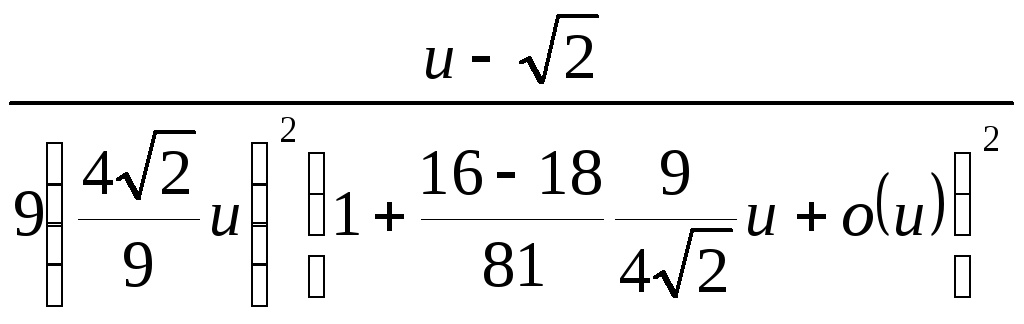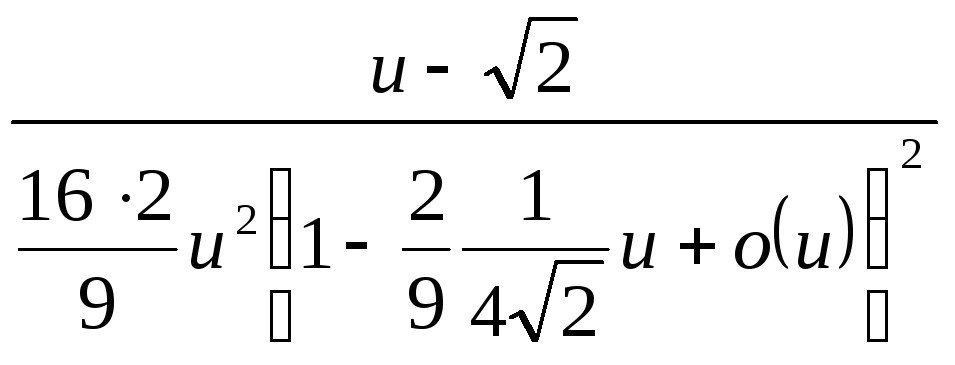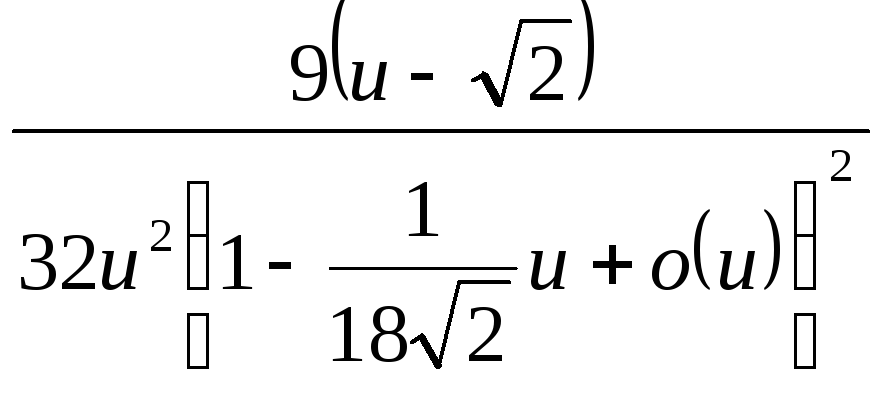По теореме единственности имеем: =. Откуда получаем, что коэффициент при равен , следовательно .

 Окончательно =

1 = = = =

2 Теорема 2(§16П) Пусть функция f в области G регулярна, прчем , . Чтобы в области G существовали ветви регулярной функции , необходимо и достаточно, чтобы для любого замкнутого кусочно-гладкого контура нашлось целое число такое, что .

3 Определение. Изолированная особая точка функции называется устранимой особой точкой, если существует конечный предел .

4 Теорема (единственности). Пусть функция регулярна в области . Пусть существует последовательность различных точек , сходящаяся к некоторой точке и такая, что . Тогда на области G.

5 , где - коэффициент разложения функции в ряд Лорана с центром в бесконечности.

6 Определение. Изолированная особая точка функции называется полюсом, если существует предел .

7 Теорема (Коши о вычетах). Пусть дана область с кусочно-гладкой положительно ориентированной границей . Пусть функция определена и регулярна на всюду, за исключением конечного числа изолированных особых точек (при этом имеется в виду, что, если , то ) и пусть к тому же функция непрерывно продолжима на границу области . Тогда справедлива формула .

8 Определение. Пусть изолированная особая точка функции , . Пусть - положительно ориентированная окружность, причем . Тогда вычетом функции в точке называется число .

9 , где - коэффициент разложения функции в ряд Лорана с центром в конечной точке при .
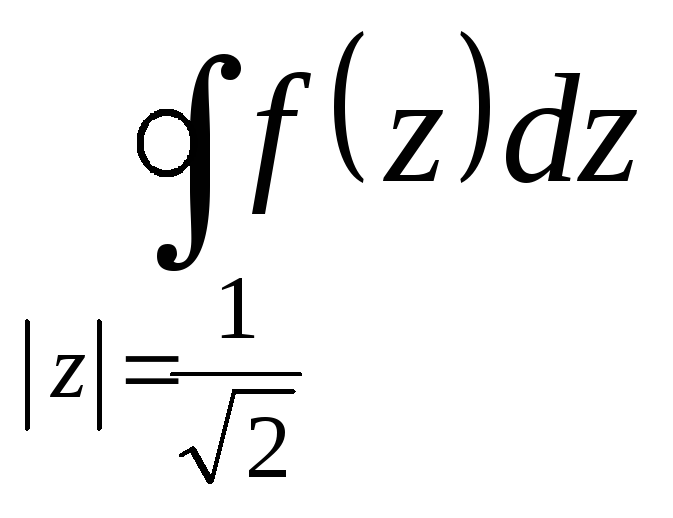