
kontra_po_tfkp_za_03-04_gg_s_resheniami / z4_v34
.doc
2003/2004 34
|
4 |
Применяя
теорию вычетов вычислить интеграл
|
Шабунин, Сидоров стр. 140 – 145 (примеры 6 стр. 144), Половинкин стр. 103 – 108 (пример 3 стр. 107 – 108)
Замечая, что
![]() =
=
![]() =
=
![]() ,
,
для решения задачи
достаточно вычислить несобственный
интеграл
![]()
и воспользоваться формулой
![]() =
=
![]() =
=
![]() .
(1)
.
(1)
Для того чтобы
применить теорему Коши1
о вычетах2,
вводим функцию комплексной переменной
![]()
и строим контур,
состоящий из отрезка вещественной оси
![]() и полуокружности
и полуокружности
![]() ,
выбрав
,
выбрав
![]() так, чтобы все особые точки
так, чтобы все особые точки
![]()
![]() функции
функции
![]() ,
лежащие в верхней полуплоскости,
оказались внутри контура. Тогда по
теореме Коши о вычетах
,
лежащие в верхней полуплоскости,
оказались внутри контура. Тогда по
теореме Коши о вычетах
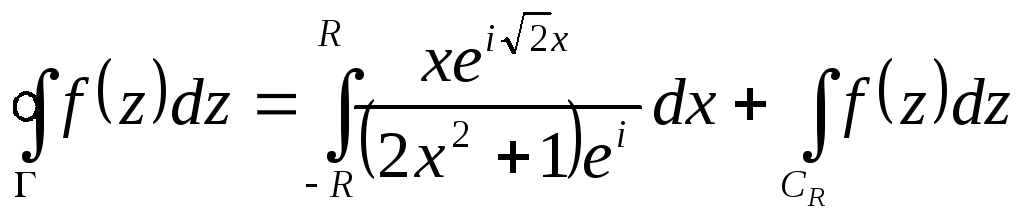 =
=
![]() .
(2)
.
(2)
Переходим к
пределу при
![]() .
Так как в нашем случае
.
Так как в нашем случае
![]() есть
правильная рациональная дробь и
есть
правильная рациональная дробь и
![]() ,
то условия леммы Жордана3
выполнены и, следовательно,
,
то условия леммы Жордана3
выполнены и, следовательно,
![]() .
.
Поскольку правая
часть в (2) не зависит от
![]() ,
имеем
,
имеем
![]() =
=
![]() ,
(3)
,
(3)
где
![]() - особые точки функции
- особые точки функции
![]() ,
лежащие в верхней полуплоскости.
,
лежащие в верхней полуплоскости.
Находим особые
точки функции
![]() =
=
 как нули (1-го порядка) ее знаменателя:
как нули (1-го порядка) ее знаменателя:
![]() и
и
![]() .
Таким образом, точки
.
Таким образом, точки
![]() и
и
![]() - полюса4
1-го порядка (ПП – простые полюса).
- полюса4
1-го порядка (ПП – простые полюса).
Вычисляем вычет
в простом полюсе
![]() по формуле
по формуле
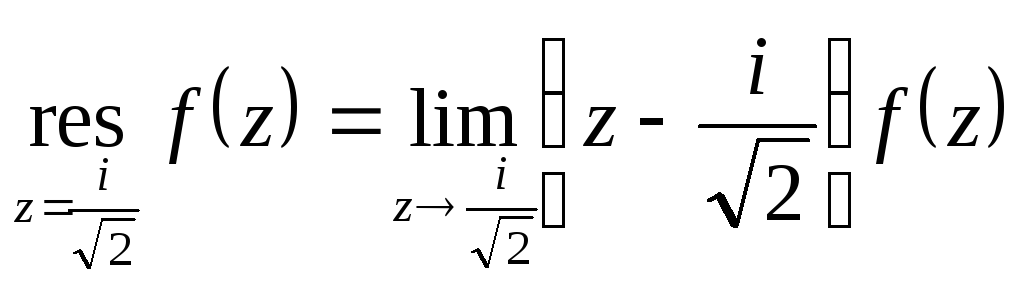 .
Получаем
.
Получаем
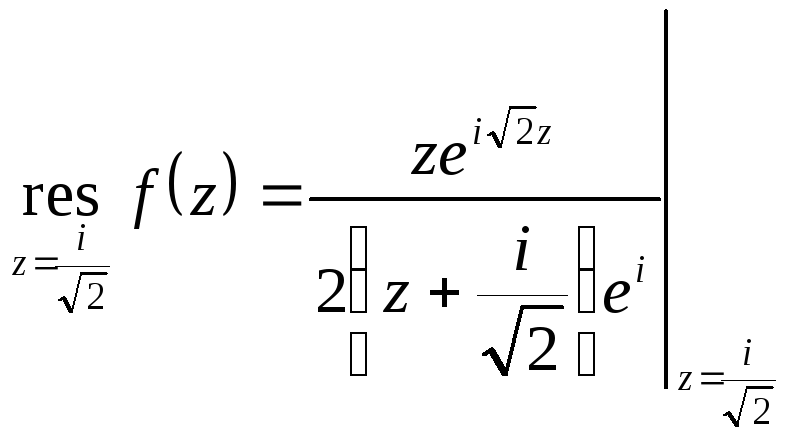 =
=
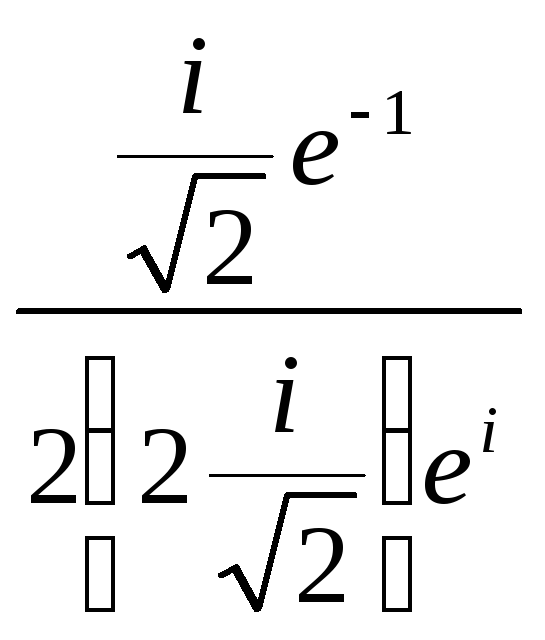 =
=
![]()
Вычисляем несобственный интеграл по формуле (3):
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() .
.
Используя формулу (1), находим искомый интеграл:
![]() =
=
![]() =
=![]() =
=
![]() =
=
![]() =
=
![]()
Ответ:
![]() =
=
![]()
1
Теорема (Коши о вычетах). Пусть дана
область
![]() с кусочно-гладкой положительно
ориентированной границей
с кусочно-гладкой положительно
ориентированной границей
![]() .
Пусть функция
.
Пусть функция
![]() определена и регулярна на
определена и регулярна на
![]() всюду, за исключением конечного числа
изолированных особых точек
всюду, за исключением конечного числа
изолированных особых точек
![]() (при этом имеется в виду, что, если
(при этом имеется в виду, что, если
![]() ,
то
,
то
![]() )
и пусть к тому же функция
)
и пусть к тому же функция
![]() непрерывно продолжима на границу
области
непрерывно продолжима на границу
области
![]() .
Тогда справедлива формула
.
Тогда справедлива формула
![]() .
.
2
Определение. Пусть изолированная
особая точка
![]() функции
функции
![]() ,
,
![]() .
Пусть
.
Пусть
![]() - положительно ориентированная
окружность, причем
- положительно ориентированная
окружность, причем
![]() .
Тогда вычетом функции
.
Тогда вычетом функции
![]() в точке
в точке
![]() называется число
называется число
![]() .
.
3
Лемма (Жордан). Пусть
![]() - непрерывная функция на замкнутом
множестве
- непрерывная функция на замкнутом
множестве
![]() .
Пусть число
.
Пусть число
![]() и
и
![]() ,
,
![]() - семейство полуокружностей в верхней
полуплоскости. Обозначим
- семейство полуокружностей в верхней
полуплоскости. Обозначим
![]() при
при
![]() .
Если
.
Если
![]() ,то
,то
![]() .
.
4
Определение. Изолированная особая
точка
![]() функции
функции
![]() называется
полюсом, если существует предел
называется
полюсом, если существует предел
![]() .
.
