14) Понятие комплексного числа в матричной форме, его вещественная и мнимая часть.

Комплексные числа можно также определить как семейство вещественных матриц вида

с обычным матричным сложением и умножением. Действительной единице будет соответствовать

мнимой единице —

15) Понятие комплексного числа в тригонометрической форме, его вещественная и мнимая часть.

Если вещественную x и мнимую y части комплексного числа выразить через модуль и аргумент(,), то всякое комплексное число, кроме нуля, можно записать в тригонометрической форме

16) Модуль и аргумент комплексного числа.

Модулем комплексного числа z ϵ C называется неотрицательное действительное число

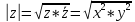равное арифметическому квадратному корню из неотрицательного действительного числа .

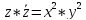Очевидно, модуль комплексного числа z равен длине r вектора z.

Аргументом ненулевого комплексного числа z ϵ C называется (любой) угол от положительного направления действительной оси до вектора z. Множество всех таких углов обозначается Arg z.

Главным значением аргумента комплексного числа z ϵ C называется то из значений аргумента, которое принадлежит промежутку (-π;π]. Главное значение аргумента обозначается arg z.

(Аргумент числа 0 не определяется.)

17) Геометрическое представление комплексных чисел.

Двумерный вектор z = (x; y) = x + y*i изображается как радиус-вектор с началом в начале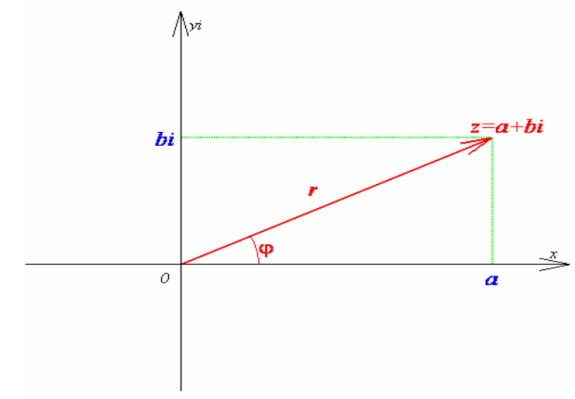

координат

Это и есть "геометрическое представление" комплексного числа.

Две координатные оси плоскости C получают специальные названия: ось, на которой располагаются все действительные числа [векторы x = (x,0)], называется действительной осью, а ось, на которой располагаются чисто мнимые числа [векторы y*i = (0,y )],— мнимой осью.

18) Умножение, сложение, деление комплексных чисел в тригонометрической форме.

Произведение

Частное

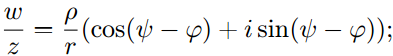
Сложение

19) Умножение, сложение, деление комплексных чисел в алгебраической форме.

Сложение

Вычитание

Умножение

Деление

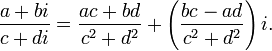
20) Умножение, сложение, деление комплексных чисел в показательной форме комплексного числа.

21) Сопряженное комплексное число.

Два комплексных числа a + b·i и a - b·i называются сопряженными. Сопряженные комплексные числа в сумме дают действительное число 2a.

22) Возведение комплексного числа в степень.

23) Корень степени n из комплексного числа.

В случае же, если z ∈ C – комплексное число, то для любого натурального числа n выражение всегда имеетсмысли обозначает все множествокорнейn-й степени из комплексного числа z.

Обозначение: , где– все nкорнейn-й степени из комплексного числа z, так что по определению.

В частности, при n=2 существуют ровно два корня из комплексного числа z и легко видеть, что, если –квадратныйкорень из комплексного числа z, то, т.е. оба корняиявляются противоположнымикомплекснымичислами, поэтому вместозаписиприменяютзапись.

24) Группа корней степени n из единицы. Сумма всех корней из единицы степени n.

Применяя предложение 32.3 к комплексному числу w = 1, мы сразу получаем, что существует ровно n различных решений уравнения z_n= 1 (n значений корня n-й степени из 1):Все z_k располагаются на единичной окружности, в вершинах правильного n-угольника.

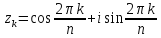k = 0,..,n-1

Главным значением корня n-й степени из 1 является z0= 1

25) Многочлен над полем. Степень, коэффициенты многочлена. Равные многочлены. Сумма, произведение многочленов.

Многочленом (или полиномом) степени n над полем P; от переменной x; называется выражение вида f(x) = f₀ + f₁x + f₂x²+ …+ f_nxⁿ

Два многочлена f (x) и g(x) (над одним и тем же полем P и от одной и той же переменной x) называются равными (это обозначается f (x) = g(x) или короче f = g), если

1) их степени одинаковы;

2) все соответствующие коэффициенты равны

26) Деление с остатком. Остаток, неполное частное, их степени.

Пусть P — поле. f (x), g (x) — два многочлена с коэффициентами из P [f (x) 6 = 0], тогда существуют (однозначно определенные) многочлены q(x), h(x) из P [x], такие, что g(x) = f (x)q(x) + h(x).

27) Наибольший общий делитель.

Пусть K — целостное кольцо; a ,b ∈ K.

Пусть элемент d является общим делителем элементов a и b, таким, что для него существует линейное представление (с коэффициентами из K) через данные элементы a и b:

d = au + bv; u, v ∈ K

Тогда d ∈ НОД(a,b):

28) Значения многочлена и корни. Теорема Безу.

Корнем многочлена f (x) ∈ P [x] называется корень соответствующей полиномиальной функции

f : P -> P; т. е. такой элемент c ∈ P, что значение f(c) = 0:

1. Остаток от деления многочлена

f (x) положительной степени n над полем P на многочлен первой степени (двучлен) x - c, где c ∈ P , равен значению f (c) многочлена f (x) в точке c.

2. Элемент c является корнем многочлена f (x) тогда и только тогда, когда двучлен x - c делит данный многочлен: x - c | f (x)

29) Разложимые и неприводимые многочлены над полем.

Всякий многочлен (36.18) положительной степени n над алгебраически замкнутым полем P имеет n корней (с учетом их кратностей) и разлагается в произведение n линейных сомножителей:

, где c1, c2, .. , c_s — все его (попарно различные) корни;

m₁, m₂, .. , m_s— кратности этих корней; m₁+ m₂ + .. + m_s = n.

30) Основная теорема алгебры.

Всякий многочлен положительной степени (n > 0) с комплексными коэффициентами (a_k ∈ C; k = 0,…, n; a₀≠0 имеет хотя бы один комплексный корень,

т. е. всегда найдется такое число z₀ ∈ C, что f(z₀) = 0)

31) Схема Горнера.

Так называемая схема Горнера является алгоритмом, в значительной степени упрощающим вычисление значений многочлена. Этот алгоритм основан на первом утверждении теоремы Безу [f(x)=(x-c)q(x)+f(c), согласно которой f (c) есть остаток от деления многочлена f (x) на двучлен x-c].

32) Определение простого и кратного корня.

Если у многочлена есть 2 одинаковых корня, то можно сказать, что это корень кратности 2. Если 3 одинаковых корня, то корень кратности 3 и т.д. Кратность корня не может превышать степень многочлена. Корни кратности 1 называются простыми или однократными корнями.

33) Утверждение о комплексном корне многочлена с вещественными коэффициентами.

34) Алгоритм отыскания всех рациональных корней многочлена с целыми коэффициентами.

Задача отыскания рациональных корней для многочлена (42.6), с целыми коэффициентами и ненулевым свободным членом, сводится к задаче перебора всех дробей c=s/t, таких, что s∈S и t∈T где введены обозначения:

S — множество всех делителей свободного члена an

T — множество всех положительных делителей старшего коэффициента a0

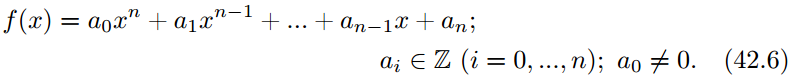35) Элементарные симметрические многочлены.

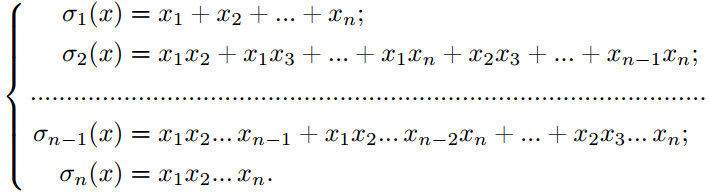
Многочлен является суммой всех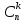возможных произведений по k (из общего числа n) переменных. Симметричность и однородность этих многочленов очевидны, как и то, что в формулах (49.4) они представлены в лексикографическом порядке.

36) Формулы Виета.

Формулы Виета позволяют однозначно (с точностью до пропорциональности) восстановить многочлен по его корням (в случае, когда их количество равно степени многочлена). Нормализованный многочлен восстанавливается однозначно: a₀ = 1; a_k= (-1)^kσ_k (k = 1,.., n)

37) Многочлены от n переменных. Лексикографическое упорядочение.

38) Теорема о симметрических многочленах.

39) Интерполяционный многочлен (в форме Лагранжа, метод Ньютона).

40) Производные многочленов.

41) Кратные корни и производные многочленов.

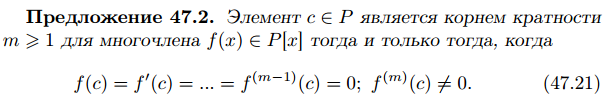
42) Система Штурма.

Ряд Штурма (система Штурма) для вещественного многочлена — последовательность многочленов, позволяющая эффективно определять количество корней многочлена на промежутке и приближённо вычислять их с помощью теоремы Штурма.

43) Теорема Штурма.

Пусть — ненулевой многочлен с вещественными коэффициентами,— некоторый ряд Штурма для него, [a, b] — промежуток вещественной прямой, причём. Тогда числоразличных корней многочлена на промежуткеравно, где— значение ряда Штурма в точке.

Ряд Штурма существует для любого ненулевого вещественного многочлена. Пусть многочлен , отличающийся от константы, не имеет кратных корней. Тогда ряд Штурма для него можно построить, например, следующим образом:

• ;

• ;

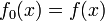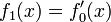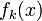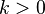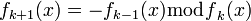• Если () имеет корни, то, где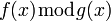— остаток от деления многочлена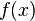на многочлен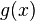вкольце многочленов 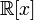, иначе.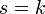

Для произвольного многочлена, отличающегося от константы, можно положить

,

и далее следовать приведенному выше способу. Здесь —наибольший общий делитель многочленов и. Если многочленесть ненулевая константа, то его ряд Штурма состоит из единственного многочлена.