
- •1) Определение определителя. Док-во
- •6) Вычисление обратной матрицы с помощью присоединенной.
- •7) Правило Крамера.
- •8) Определитель произведения матриц.
- •9) Связь обратимости и неособости.
- •10) Минор порядка k, Количество миноров порядка k. Минорный ранг матрицы. Ранговый минор.
- •11) Вторая теорема о ранге матрицы.
- •12) Метод окаймляющих миноров для вычисления ранга матрицы.
- •13) Понятие комплексного числа в алгебраической форме, его вещественная и мнимая часть.
- •14) Понятие комплексного числа в матричной форме, его вещественная и мнимая часть.
- •15) Понятие комплексного числа в тригонометрической форме, его вещественная и мнимая часть.
- •16) Модуль и аргумент комплексного числа.
- •17) Геометрическое представление комплексных чисел.
- •24) Группа корней степени n из единицы. Сумма всех корней из единицы степени n.
- •44) Задача отделения корней многочлена.
- •45) Примитивные многочлены.
- •47) Признак Эйзенштейна.
8) Определитель произведения матриц.
Определитель произведения матриц равен произведению определителей матриц-сомножителей: det(A*B)=det(A)*det(B).
9) Связь обратимости и неособости.
Пусть матрица A обратима, т.е. существует такая матрица B, что A*B=B*A=E. Применяя свойство определителя произведений матриц, получим: det(A)*det(B)=1.
Из этого следует, что det(A) не равен нулю то есть матрица A является неособой.
Обратно, пусть A-неособа. Рассмотрим присоединенную матрицу A˅ и поделим ее на скаляр det(A) не равный нулю, т.е. образуем матрицу:
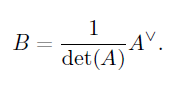
После некоторых операций получим:
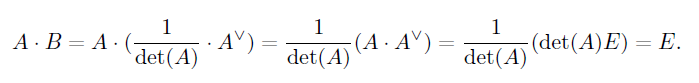
Совершенно аналогично получается B*A=E. Значит, матрица A обратима.
10) Минор порядка k, Количество миноров порядка k. Минорный ранг матрицы. Ранговый минор.
1) Пусть A-прямоугольная матрица размера m x n, k-натуральное число не превышающее min(m,n).
Рассмотрим какие-либо k строк матрицы A с номерами i1<i2<...<ik и какие либо k столбов с номерами j1<j2<...<jk, а также (k x k)-матрицу, получаемую на пересечении указанных строк и столбцов. Определитель этой матрицы называется минором порядка k для матрицы A и обозначается:
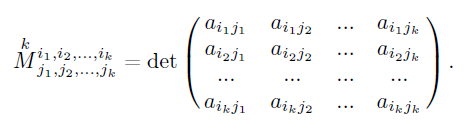
2) Для подсчета количества миноров порядка k воспользуемся комбинаторной формулой для числа сочетаний (из n элементов по k)
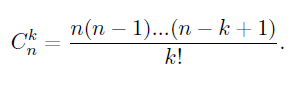 (количество
упорядоченных по возр. наборов из k
столбцов)
(количество
упорядоченных по возр. наборов из k
столбцов)
Аналогично
количество упорядоченных по возр.
наборов из номеров строк равно
![]()
При
образовании минора k-го
порядка любой из подсчитанных выше
наборов строк может сочетаться с любым
из наборов столбцов. Поэтому общее
количество миноров порядка k
будет равно произведению
![]() .
.
3) Минорным рангом матрица A называется наивысший порядок миноров этой матрицы, отличных от нуля. (Если таковых вообще нет, то минорный ранг считается равным нулю). Обозн. rankмин(A)
4) Если rankмин(A)=r, то всякий ненулевой минор порядка r называется ранговым минором для матрицы A. (где r - неотрицательное целое число)
11) Вторая теорема о ранге матрицы.
Все четыре ранга (ступенчатый, столбцовый, строчный и минорный) совпадают.
12) Метод окаймляющих миноров для вычисления ранга матрицы.
Описание работы алгоритма:
1. Если A = O, то rank(A) = 0, рангового минора не существует.
2.
Если A≠O, то выбираем какой-либо минор
первого порядка
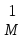 (т. е. элемент матрицы A), отличный от
нуля.
(т. е. элемент матрицы A), отличный от
нуля.
3.
Перебираем миноры второго порядка,
окаймляющие выбранный минор первого
порядка, до тех пор пока не переберем
все (и они все окажутся нулевыми) или
пока не обнаружим ненулевой минор
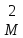 . В первом случае rank(A) = 1 и в качестве
рангового можно предъявить выбранный
на предыдущем шаге ненулевой минор
. В первом случае rank(A) = 1 и в качестве
рангового можно предъявить выбранный
на предыдущем шаге ненулевой минор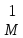 .
Во втором случае перебираем миноры
третьего порядка, окаймляющие выбранный
на предыдущем шаге ненулевой минор
.
Во втором случае перебираем миноры
третьего порядка, окаймляющие выбранный
на предыдущем шаге ненулевой минор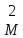 ; и т. д.
; и т. д.
4.
Остановка происходит, либо когда
найденный на шаге с номером r ненулевой
минор
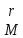 не имеет окаймляющих [ это бывает, если
r = min(m, n) ], либо когда все миноры
не имеет окаймляющих [ это бывает, если
r = min(m, n) ], либо когда все миноры ,
окаймляющие минор
,
окаймляющие минор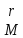 равны нулю. В обоих случаях выводим
равны нулю. В обоих случаях выводим
Ответ:
rank(A) = r.
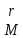 — ранговый минор.
— ранговый минор.
13) Понятие комплексного числа в алгебраической форме, его вещественная и мнимая часть.
Комплексным числом называется выражение вида z = x+y*i, где x и y - действительные числа, а
i - мнимая единица.
