Линейное программирование111.rtf (2)

Вариант 289

a=1 b=4 c=2 d=1

ЗАДАНИЕ №1

1. Решить задачу оптимизации. Найти оптимальное решение.

2. Провести анализ чувствительности решения к значениям ограничений ресурсов.

3. Провести параметрический анализ небазисного ресурса.

4. Определить базис по продуктам в момент входа небазисных ресурсов в базис.

Станки №	Затраты времени на одно изделие				Месячный фонд машинного времени
	1	2	3	4
1	2	6	6	7	5000
2	17	17	12	16	16000
3	15	13	17	13	42000
Прибыль на одно изделие	15	16	17	17

Решение:

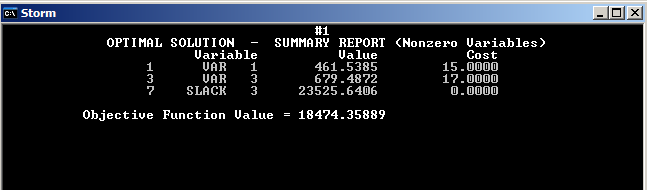
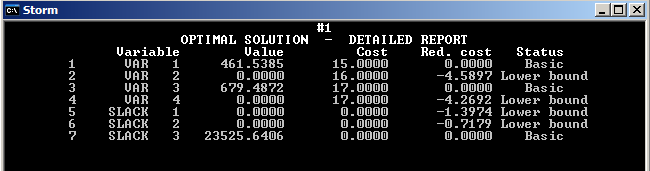
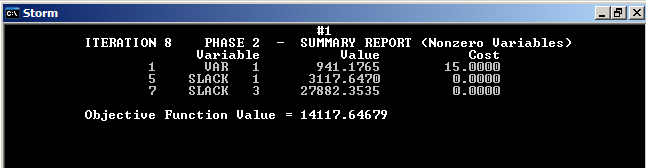
Оптимальное решение: производим 2 изделия, первое - в количестве 461 стоимостью 15, второе – в количестве 679 стоимостью 17.

Целевая функция 18474,64

Базисный ресурс 3.

Анализ чувствительности:

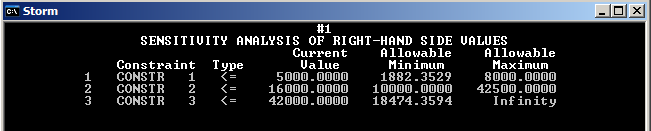
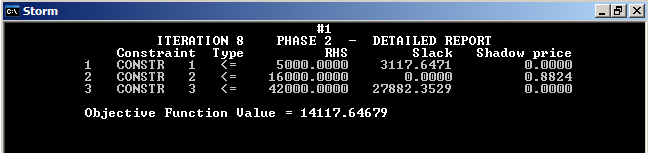
Первый ресурс не будут входить в базис, когда его количество больше 1882 и меньше 8000.

Второй ресурс не будет входить в базис, когда его количество больше 10000 и меньше 42500.

Третий ресурс будет входить в базис, когда его количество больше 18474.

Параметрический анализ небазисного ресурса: первого.

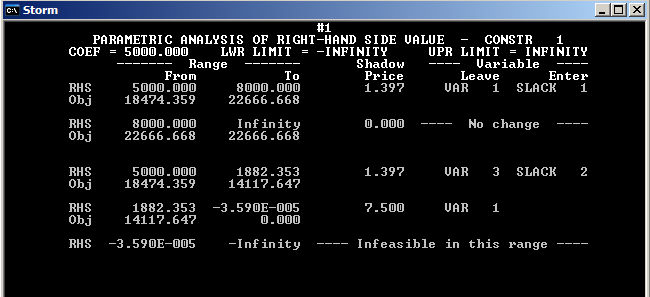
Когда количество первого ресурса будет больше 0, но меньше 8000 – при изменении ресурса на 1, цена будет меняться на 1,40.

Параметрический анализ небазисного ресурса: второго.

Когда количество второго ресурса будет больше 0, но меньше 42500 – при изменении ресурса на 1, цена будет меняться на 0,72.

Базис по продуктам в момент входа небазисных ресурсов в базис:

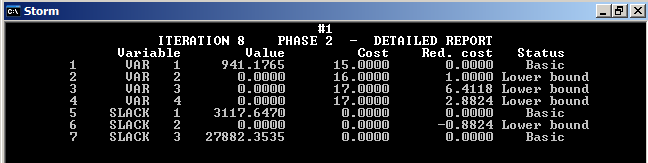
Если в базис включим значение первого ресурса, то целевая функция будет иметь значение 14117,65.

Будем производить только одно изделие в количестве 941 стоимостью 15.

Базисными ресурсами будут ресурс 1 и ресурс 3.

Если мы увеличим ресурс 2 на единицу, то целевая функция изменится на 0,88.

ЗАДАНИЕ №2.

1. Найти оптимальную расстановку рабочих по операциям на участке, их выработка по операциям (до 150 варианта, время выполнения к_m-й операции – после 150 варианта) указана в таблице

№ операции	Рабочие
	1	2	3	4	5	6
1	12	16	16	17	13	14
2	17	12	17	28	52	56
3	14	17	52	13	13	15
4	16	17	2	14	24	14
5	15	52	24	15	26	13
6	14	48	26	16	28	16

Решение:

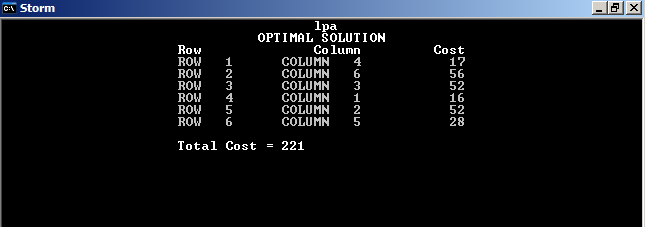
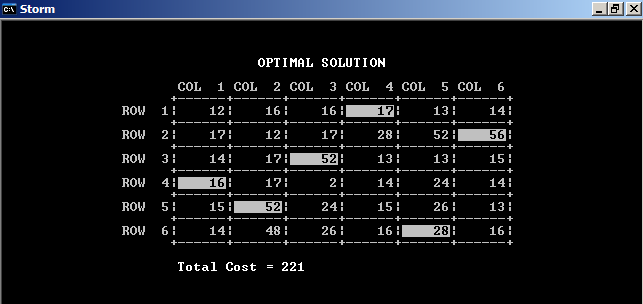
Оптимальная расстановка:

1 рабочий – 4 операция;

2 рабочий – 5 операция;

3 рабочий – 3 операция;

4 рабочий – 1 операция;

5 рабочий – 6 операция;

6 рабочий – 2 операция.

Выработка по операциям составляет – 221.

ЗАДАНИЕ №3.

1. Решить транспортную задачу. Найти оптимальное решение. В таблице приведены стоимости перевозки единицы груза.

2. Определить величину неудовлетворенного спроса.

3. Определить величину нераспределенного товара на складах.

4. Определить дополнительный вариант распределения поставок.

Отправители	получатели						Предложение
	1	2	3	4	5	6
1	12	17	16	14	13	17	20
2	17	17	12	12	12	24	14
3	14	2	17	14	52	13	19
4	12	21	52	15	24	15	16
5	1З	14	56	17	4	24	20
6	1	24	28	16	12	2	21
Спрос	19	16	20	20	14	21

Решение:

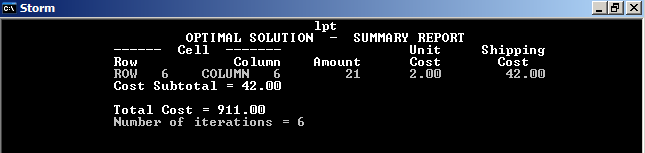
Оптимальное решение:

1 поставщик везет 3 покупателю 6 ед. стоимостью 16 сумма 96

4 покупателю 14 ед. стоимостью 14 сумма 196

Итого 292

2 поставщик везет 3 покупателю 14 ед. стоимостью 12 сумма 168

Итого 168

3 поставщик везет 2 покупателю 16 ед. стоимостью 2 сумма 32

4 покупателю 3 ед. стоимостью 14 сумма 42

Итого 74

4 поставщик везет 1 покупателю 13 ед. стоимостью 12 сумма 156

4 покупателю 3 ед. стоимостью 15 сумма 45

Итого 201

5 поставщик везет 1 покупателю 6 ед. стоимостью 13 сумма 78

5 покупателю 14 ед. стоимостью 4 сумма 56

Итого 134

6 поставщик везет 6 покупателю 21 ед. стоимостью 2 сумма 42

Итого 42

Общая сумма расходов по поставке составляет 911

Спрос удовлетворен. Товар на складах распределен полностью.

Дополнительного варианта распределения поставок не требуется.

ЗАДАНИЕ №4.

1. Рассчитать сетевой график работ. Диапазон колебаний при вероятностном времени – три единицы.

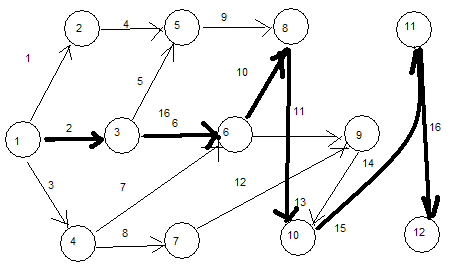
2. Нарисовать схему сетевого графика.

3. Указать критический путь.

4. Определить время выполнения всего комплекса работ при точном и вероятностном времени.

№ работ	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Длительность работы	2	4	1	2	2	6	3	12	8	7	6	6	7	4	4	5
Начальное событие	1	1	1	2	3	3	4	4	5	6	6	7	8	9	10	11
Конечное событие	2	3	4	5	5	6	6	7	8	8	9	9	10	10	11	12

Решение:

Комплекс работ при точном времени.

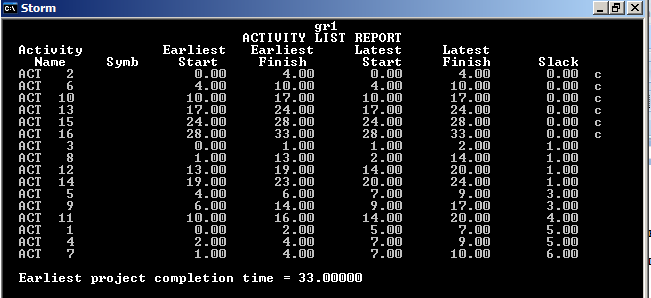
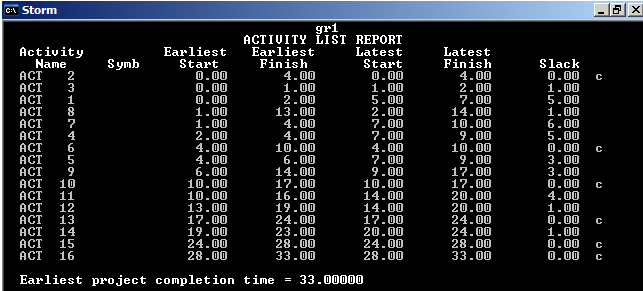
Критический путь 2,6,10,13,15,16.

Время выполнения работы 33.

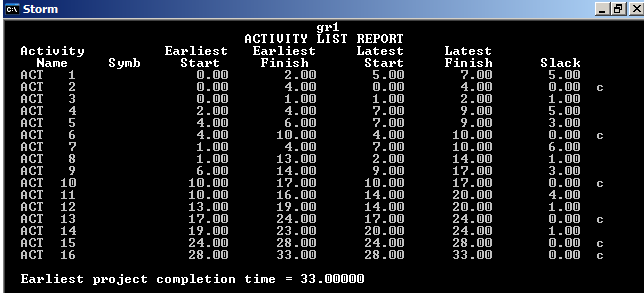
Комплекс работ при вероятностном времени.

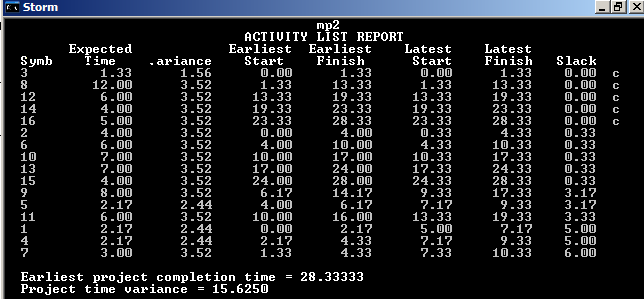
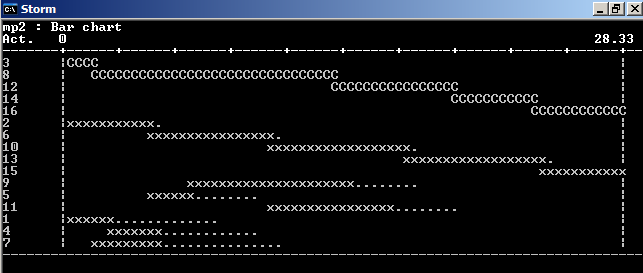
Критический путь 3,8,12,14,16

Время выполнения работы 28,33.

ЗАДАНИЕ №5.

1. Построить модель линейной регрессии

2. Рассчитать коэффициенты корреляции. Провести корреляционный анализ.

№предприятия	1	2	3	4	5
Качество продукции	92	98	101	185	212
Качество рабочей силы	91	106	101	189	211
Качество оборудования	258	414	288	444	580

6	7	8	9	10	11	12
262	356	150	167	207	190	252
262	352	146	167	203	190	249
760	910	410	456	483	436	910

Решение:

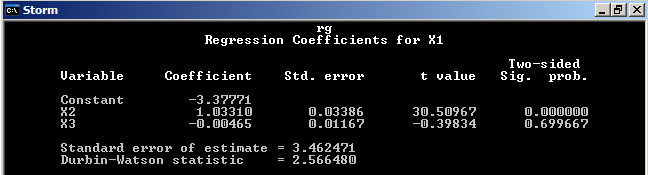
Линейная регрессия имеет модель

Х1= а*х2+b*x3+c

X1=-3.37771 + 1.03310 x2 – 0.00465 x3

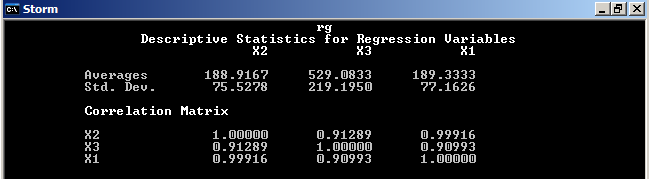
В корреляционной матрице коэффициенты зависимости

Х1 от Х2 0.99916; Х1 от Х3 0.90993.