
дом работа 2 интегралы
.pdf
ȼɚɪɢɚɧɬ ʋ1
1. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɚɹ ɢɡ ɭɤɚɡɚɧɧɵɯ ɮɭɧɤɰɢɣ ɹɜɥɹɟɬɫɹ ɩɟɪɜɨɨɛɪɚɡɧɨɣ ɞɥɹ ɮɭɧɤɰɢɢ f (x) = x2 sin(x) ɧɚ ɩɪɨɦɟɠɭɬɤɟ f f :
a)x2 cos (x) 2 cos (x) 2 x sin(x)
b)x3 cos (x)
3
c) ex cos (x) x3
3
2. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɨɣ ɢɡ ɢɧɬɟɝɪɚɥɨɜ "ɧɟ ɛɟɪɟɬɫɹ":
´ |
x |
|
´ |
|
2 |
|
|
´ |
|
´ |
|
|
µ |
|
µ |
|
x |
|
|
µ |
1 x dx d) |
µ |
|
||
a) µ |
|
dx |
b) |
µ |
e |
|
dx |
c) |
µ |
µ |
y dx |
|
x |
|
|||||||||||
µ |
3 |
|
|
¶ |
|
|
|
|
¶ |
|
¶ |
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
3. Ɉɩɪɟɞɟɥɢɬɟ, ɧɟ ɜɵɱɢɫɥɹɹ, ɤɚɤɨɣ ɢɡ ɞɜɭɯ ɢɧɬɟɝɪɚɥɨɜ ɛɨɥɶɲɟ: |
|
|
||||||||||
´1 |
|
|
|
|
´1 |
|
|
|
|
|
|
|
a) µ |
|
x dx |
|
b) |
µ x2 dx |
|
|
|
|
|
||
¶0 |
|
|
|
|
¶0 |
|
|
|
|
|
|
|
´1
4. ɇɚ ɤɚɤɨɦ ɪɢɫɭɧɤɟ ɢɡɨɛɪɚɠɟɧɚ ɮɢɝɭɪɚ, ɩɥɨɳɚɞɶ ɤɨɬɨɪɨɣ ɱɢɫɥɟɧɧɨ ɪɚɜɧɚ µ (1 x) dx ?
¶0
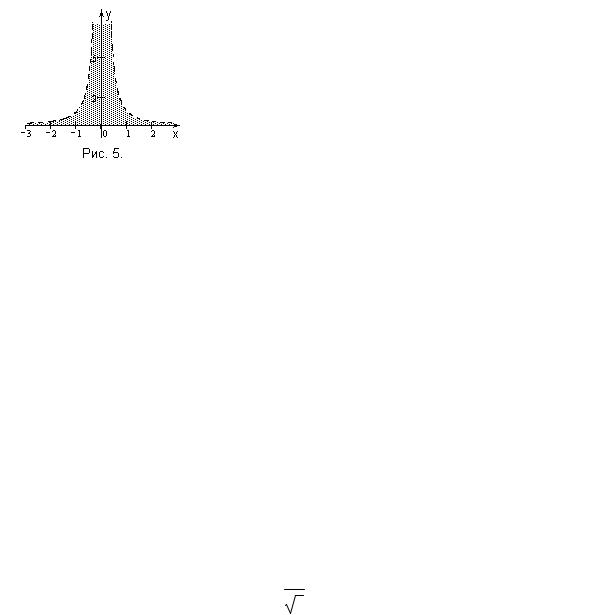
5. Ʉɚɤɢɟ ɢɡ ɢɧɬɟɝɪɚɥɨɜ ɹɜɥɹɸɬɫɹ ɧɟɫɨɛɫɬɜɟɧɧɵɦɢ?
|
´ |
x ex dx |
´f |
1 |
|
´2 |
´1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||
a) |
µ |
b) µ |
dx |
c) µ x ln(x) dx |
d) µ |
|
|
|
|
|
dx |
|||
|
|
|
|
|||||||||||
µ |
|
|
|
|
|
|
||||||||
|
|
µ |
|
4 |
|
¶0 |
µ |
|
|
x |
||||
|
¶ |
|
¶1 |
x |
|
|
|
¶ 1 |
|
|
|
|
|
|
6. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ f (x) = x2 |
1 |
3x . |
||||
|
|||||||
|
|
|
|
|
|
x |
|
7. |
ɉɨɞɫɱɢɬɚɣɬɟ ɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ f (x) = |
2x |
ɧɚ ɩɪɨɦɟɠɭɬɤɟ [-1, 2]. |
||||
|
|||||||
|
|
|
|
x2 1 |
|||
|
´f |
1 |
|
|
|
|
|
8. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ µ |
|
dx . |
||||
|
|||||||
|
µ |
x |
|||||
|
¶ |
e |
|||||
|
0 |
|
|
|
|
|
|
|
´1 |
1 |
|
|
|
|
|
9. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ µ |
|
dx . |
||||
|
µ |
3 x |
|||||
¶ 1
10. ȼɵɱɢɫɥɢɬɟ ɩɥɨɳɚɞɶ ɮɢɝɭɪɵ, ɨɝɪɚɧɢɱɟɧɧɨɣ ɥɢɧɢɹɦɢ:
y = x2
y = 2 x2
ȼɚɪɢɚɧɬ ʋ 2
1. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɚɹ ɢɡ ɭɤɚɡɚɧɧɵɯ ɮɭɧɤɰɢɣ ɹɜɥɹɟɬɫɹ ɩɟɪɜɨɨɛɪɚɡɧɨɣ ɞɥɹ ɮɭɧɤɰɢɢ f (x) = x2 ex ɧɚ ɩɪɨɦɟɠɭɬɤɟ f f :
a)2x ex
b)x3 ex
3
c)x2 ex 2 x ex 2 ex
2. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɨɣ ɢɡ ɢɧɬɟɝɪɚɥɨɜ "ɧɟ ɛɟɪɟɬɫɹ":
|
´ |
|
x |
|
|
´ |
1 x |
2 |
|
|
´ |
|
´ |
|
|
|
a) |
µ |
|
dx |
b) |
µ |
|
dx |
c) |
µ |
1 x dx d) |
µ |
y x |
2 |
dx |
||
µ |
3 |
|
µ |
e |
|
µ |
µ |
|
||||||||
|
¶ |
|
|
|
|
¶ |
|
|
|
|
¶ |
|
¶ |
|
|
|
3. Ɉɩɪɟɞɟɥɢɬɟ, ɧɟ ɜɵɱɢɫɥɹɹ, ɤɚɤɨɣ ɢɡ ɞɜɭɯ ɢɧɬɟɝɪɚɥɨɜ ɛɨɥɶɲɟ: |
|
|
|
|
||||||||||||
|
´1 |
|
|
|
|
´1 |
|
|
|
|
|
|
|
|
|
|
a) |
µ x dx |
b) |
µ x3 dx |
|
|
|
|
|
|
|
|
|||||
|
¶0 |
|
|
|
|
¶0 |
|
|
|
|
|
|
|
|
|
|
´1
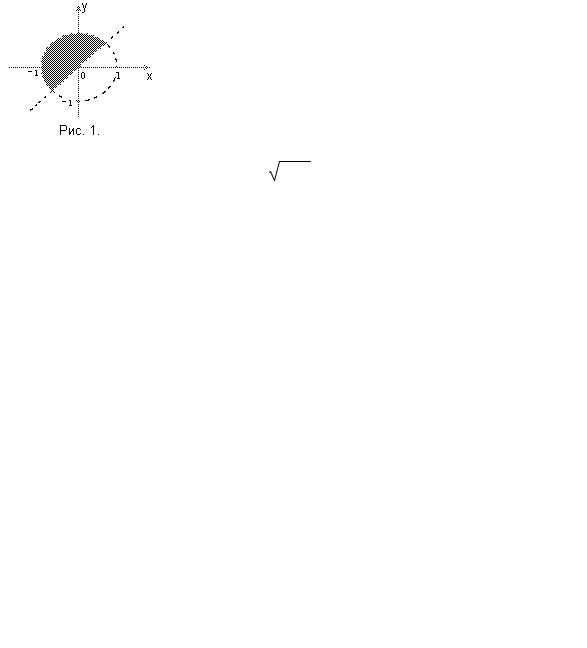
4. ɇɚ ɤɚɤɨɦ ɪɢɫɭɧɤɟ ɢɡɨɛɪɚɠɟɧɚ ɮɢɝɭɪɚ, ɩɥɨɳɚɞɶ ɤɨɬɨɪɨɣ ɱɢɫɥɟɧɧɨ ɪɚɜɧɚ 4 µ (1 x) dx ?
¶0

5. |
Ʉɚɤɢɟ ɢɡ ɢɧɬɟɝɪɚɥɨɜ ɹɜɥɹɸɬɫɹ ɧɟɫɨɛɫɬɜɟɧɧɵɦɢ? |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
´ |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
µ |
x2 |
´ |
|
1 |
|
´ |
|
|
x ln |
|
dx d) |
´ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
a) |
µ |
|
dx |
b) µ |
|
|
dx c) |
µ |
|
|
x |
µ |
|
x |
dx |
||||||||
|
|
|
|
||||||||||||||||||||
|
µ |
sin(x) |
µ |
|
ex |
¶ 2 |
|
|
|
|
|
|
¶ 1 |
|
|
||||||||
|
¶ |
|
|
¶ f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
|
|
|
f (x) = x3 |
2 |
ex . |
|||||||||||||||||
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
||
7. |
ɉɨɞɫɱɢɬɚɣɬɟ ɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ f (x) = |
x2 |
ɧɚ ɩɪɨɦɟɠɭɬɤɟ [0, 2]. |
||||||||||||||||||||
|
|
||||||||||||||||||||||
x3 1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
´f |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
8. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ µ |
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
µ |
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
¶1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
´3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
9. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ |
µ |
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
µ |
|
5 x |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
¶ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
10. ȼɵɱɢɫɥɢɬɟ ɩɥɨɳɚɞɶ ɮɢɝɭɪɵ, ɨɝɪɚɧɢɱɟɧɧɨɣ ɥɢɧɢɹɦɢ:
y = 4 x2
y = x2 2x
ȼɚɪɢɚɧɬ ʋ 3
1. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɚɹ ɢɡ ɭɤɚɡɚɧɧɵɯ ɮɭɧɤɰɢɣ ɹɜɥɹɟɬɫɹ ɩɟɪɜɨɨɛɪɚɡɧɨɣ ɞɥɹ ɮɭɧɤɰɢɢ
f (x) = x2 ln(x) |
ɧɚ ɩɪɨɦɟɠɭɬɤɟ 1 f : |
||||||||
a) |
2x |
1 |
|
|
|
|
|||
x |
|
|
|
||||||
|
|
|
|
|
|
|
|
||
b) |
1 |
x3 ln(x) |
1 |
x3 |
|||||
|
|
||||||||
|
3 |
|
|
|
|
9 |
|
||
c) |
|
x3 |
ex |
|
|
|
|||
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|||
2. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɨɣ ɢɡ ɢɧɬɟɝɪɚɥɨɜ "ɧɟ ɛɟɪɟɬɫɹ":
´ |
x |
|
|
´ |
|
3 y |
2 |
|
´ |
|
´ |
x |
|
|
|
|
µ |
|
|
µ |
|
|
|
µ |
1 x dx d) |
µ |
x |
2 |
|
||||
a) µ |
|
|
dx |
b) |
µ |
e |
|
dy |
c) |
µ |
µ |
e |
|
dx |
||
3 |
y |
|
|
|||||||||||||
µ |
|
|
|
¶ |
|
|
|
|
¶ |
|
¶ |
|
|
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Ɉɩɪɟɞɟɥɢɬɟ, ɧɟ ɜɵɱɢɫɥɹɹ, ɤɚɤɨɣ ɢɡ ɞɜɭɯ ɢɧɬɟɝɪɚɥɨɜ ɛɨɥɶɲɟ: |
|
|
|
|
|
|||||||||||
´2 |
|
|
|
|
´2 |
|
|
|
|
|
|
|
|
|
|
|
a) µ x dx |
b) |
µ x3 dx |
|
|
|
|
|
|
|
|
||||||
¶1 |
|
|
|
|
¶1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
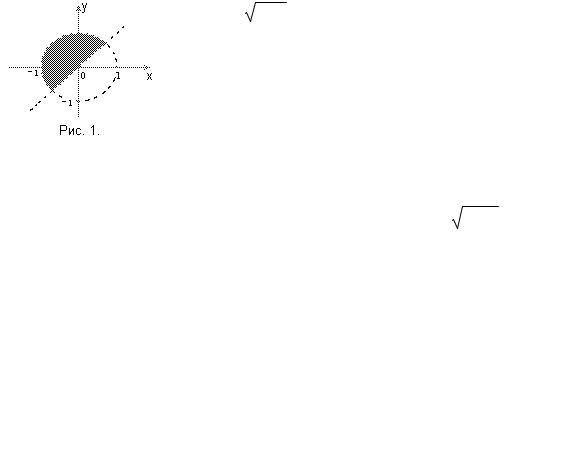
´1 |
4. ɇɚ ɤɚɤɨɦ ɪɢɫɭɧɤɟ ɢɡɨɛɪɚɠɟɧɚ ɮɢɝɭɪɚ, ɩɥɨɳɚɞɶ ɤɨɬɨɪɨɣ ɱɢɫɥɟɧɧɨ ɪɚɜɧɚ |
|
8 µ 1 y2 dy ? |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶0 |

5. |
Ʉɚɤɢɟ ɢɡ ɢɧɬɟɝɪɚɥɨɜ ɹɜɥɹɸɬɫɹ ɧɟɫɨɛɫɬɜɟɧɧɵɦɢ? |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
´ |
|
|
|
|
2 |
|
|
|
|
|
|
|
´1 |
1 |
|
|
|
|
|
|
x |
2 |
|
´ |
|
´ |
2 |
|
|
|
|
µ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
µ |
|
|
|
|
|
|
|
2 dx |
|
|
|
|
|
|
|
||||
a) |
µ |
|
|
dx b) |
µ |
|
x 4x dx c) |
µ |
|
|
|
d) µ e x |
dx |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
x |
|
|
µ |
|
7 |
x |
¶ |
|
|
|
|
|
|
||||||
|
µ |
e |
|
|
¶ |
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
f |
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
¶ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
|
|
|
f (x) = 3 x |
|
2 |
x . |
|||||||||||||
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
7. |
ɉɨɞɫɱɢɬɚɣɬɟ ɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ f (x) = (x 1)12 |
ɧɚ ɩɪɨɦɟɠɭɬɤɟ [-1, 0]. |
||||||||||||||||||
|
|
|
|
|
|
|
|
´f |
|
|
5 |
|
|
|
|
|
|
|
|
|
8. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ µ |
|
|
|
|
dx . |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
µ |
|
|
x2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
¶1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
´3 |
|
|
1 |
|
|
|
|
|
|
|
||
9. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ |
µ |
|
|
|
dx . |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
µ |
|
|
3 x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
¶0 |
|
|
|
|
|
|
|
|
|
|
|
|
10. ȼɵɱɢɫɥɢɬɟ ɩɥɨɳɚɞɶ ɮɢɝɭɪɵ, ɨɝɪɚɧɢɱɟɧɧɨɣ ɥɢɧɢɹɦɢ:
y = (x 2)3
y = 4 x 8

ȼɚɪɢɚɧɬ ʋ 4
1. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɚɹ ɢɡ ɭɤɚɡɚɧɧɵɯ ɮɭɧɤɰɢɣ ɹɜɥɹɟɬɫɹ ɩɟɪɜɨɨɛɪɚɡɧɨɣ ɞɥɹ ɮɭɧɤɰɢɢ f (x) = x 1 x2 ɧɚ ɩɪɨɦɟɠɭɬɤɟ f f :
a) |
x2 |
|
1 |
x3 |
|
|
|
|
|
||||
|
2 |
|
|
3 |
|
|
2 x
b)
2 1 x
c)1 1 x2 3
3
2. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɨɣ ɢɡ ɢɧɬɟɝɪɚɥɨɜ "ɧɟ ɛɟɪɟɬɫɹ":
|
´ |
x |
|
|
|
´ |
1 y |
2 |
|
´ |
|
|
´ |
z |
|
|
|
|
|
a) |
µ |
|
|
b) |
µ |
|
c) |
µ |
1 y dx |
d) |
µ |
x |
2 |
|
|
|
|||
µ |
1 x |
2 |
dx |
µ |
e |
dy |
µ |
µ |
e |
|
dx |
|
|
||||||
|
µ |
|
|
|
¶ |
|
|
|
¶ |
|
|
¶ |
|
|
|
|
|
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Ɉɩɪɟɞɟɥɢɬɟ, ɧɟ ɜɵɱɢɫɥɹɹ, ɤɚɤɨɣ ɢɡ ɞɜɭɯ ɢɧɬɟɝɪɚɥɨɜ ɛɨɥɶɲɟ: |
|
|
|
|
|
|
|
|
|||||||||||
|
´2 |
|
|
|
´2 |
x |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
a) |
µ x dx |
|
b) |
µ |
e |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
¶0 |
|
|
|
¶0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
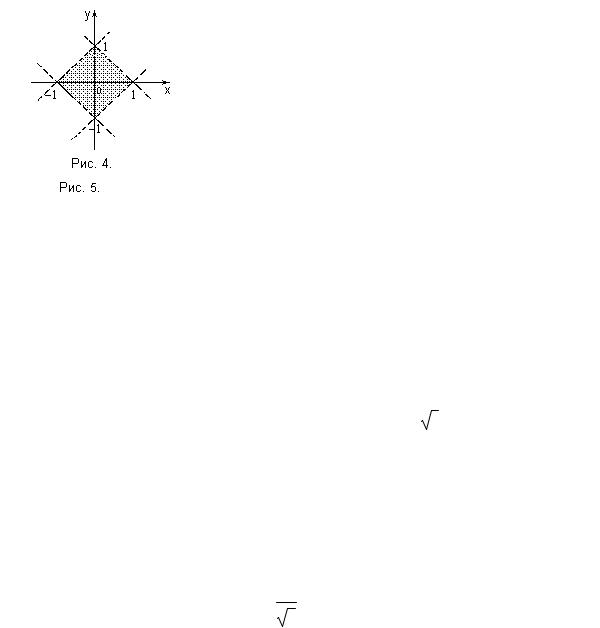
´2 |
1 |
dx ? |
||
4. ɇɚ ɤɚɤɨɦ ɪɢɫɭɧɤɟ ɢɡɨɛɪɚɠɟɧɚ ɮɢɝɭɪɚ, ɩɥɨɳɚɞɶ ɤɨɬɨɪɨɣ ɱɢɫɥɟɧɧɨ ɪɚɜɧɚ |
2 µ |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
3 |
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
5. Ʉɚɤɢɟ ɢɡ ɢɧɬɟɝɪɚɥɨɜ ɹɜɥɹɸɬɫɹ ɧɟɫɨɛɫɬɜɟɧɧɵɦɢ? |
|
||||
|
´ |
x2 dx |
´ 1 |
´x |
´e |
a) |
µ |
b) µ x 2x dx |
c) µ sin(x) dx |
d) µ x3 ln(x) dx |
|
|
µ |
|
¶ f |
¶1 |
¶0 |
|
¶ |
|
|||
6. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ f (x) = |
1 |
2 x 3 . |
||
|
|||||
|
|
|
|
x |
|
7. |
ɉɨɞɫɱɢɬɚɣɬɟ ɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ f (x) = (x 3)11 ɧɚ ɩɪɨɦɟɠɭɬɤɟ [-3, 0]. |
||||
|
´f |
7 |
|
|
|
8. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ µ |
|
dx . |
||
|
|||||
|
µ |
x8 |
|||
|
¶2 |
|
|
|
|
´0 |
1 |
9. ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ µ |
dx . |
µ |
5 x |
¶ 1 |
|
10. ȼɵɱɢɫɥɢɬɟ ɩɥɨɳɚɞɶ ɮɢɝɭɪɵ, ɨɝɪɚɧɢɱɟɧɧɨɣ ɥɢɧɢɹɦɢ:
y = 3 2 x x2
y = 0

ȼɚɪɢɚɧɬ ʋ 5
1. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɚɹ ɢɡ ɭɤɚɡɚɧɧɵɯ ɮɭɧɤɰɢɣ ɹɜɥɹɟɬɫɹ ɩɟɪɜɨɨɛɪɚɡɧɨɣ ɞɥɹ ɮɭɧɤɰɢɢ f (x) = ln(x) ɧɚ ɩɪɨɦɟɠɭɬɤɟ 0 f :
a) 1
x
b)ex
c)x ln(x) x
2. Ɉɩɪɟɞɟɥɢɬɟ, ɤɚɤɨɣ ɢɡ ɢɧɬɟɝɪɚɥɨɜ "ɧɟ ɛɟɪɟɬɫɹ":
|
´ |
|
|
´ |
|
y |
|
´ |
x |
2 |
dx |
|
´ |
x |
|
|
|
|
µ |
|
|
µ |
2 |
|
µ |
|
|
µ |
x |
2 |
|
||||
a) |
µ |
z dx |
b) |
µ |
y |
e dy |
c) |
µ |
1 e |
|
d) |
µ |
e |
|
dx |
||
|
¶ |
|
|
¶ |
|
|
|
¶ |
|
|
|
|
¶ |
|
|
|
|
3. Ɉɩɪɟɞɟɥɢɬɟ, ɧɟ ɜɵɱɢɫɥɹɹ, ɤɚɤɨɣ ɢɡ ɞɜɭɯ ɢɧɬɟɝɪɚɥɨɜ ɛɨɥɶɲɟ: |
|
|
|
|
|
|
|||||||||||
|
´2 |
|
|
|
´2 |
|
|
|
|
|
|
|
|
|
|
|
|
a) |
µ x2 dx |
|
b) |
µ x3 dx |
|
|
|
|
|
|
|
|
|
|
|
||
|
¶1 |
|
|
|
¶1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
´2 |
1 |
|
|
4. ɇɚ ɤɚɤɨɦ ɪɢɫɭɧɤɟ ɢɡɨɛɪɚɠɟɧɚ ɮɢɝɭɪɚ, ɩɥɨɳɚɞɶ ɤɨɬɨɪɨɣ ɱɢɫɥɟɧɧɨ ɪɚɜɧɚ |
1 µ |
|
dx |
? |
|
||||
|
¶ |
x |
|
|
|
0.5 |
|
|
|
5. |
Ʉɚɤɢɟ ɢɡ ɢɧɬɟɝɪɚɥɨɜ ɹɜɥɹɸɬɫɹ ɧɟɫɨɛɫɬɜɟɧɧɵɦɢ? |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
f |
|
|
´1 |
|
|
1 |
|
||
|
´ |
|
|
x |
|
´ |
|
|
|
|
´ |
5 |
|
µ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a) |
µ |
x |
2 |
dx |
|
x 4 |
x |
dx |
c) |
|
2 x |
dx |
d) µ |
e |
x |
dx |
||||||
µ |
|
e |
b) µ |
|
|
µ |
|
|
|
|||||||||||||
|
|
|
|
|
¶0 |
|
|
|
|
¶1 |
|
|
|
¶ |
|
|
|
|
||||
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
6. |
|
|
f (x) = 2 x2 |
1 |
|
3 . |
||||||||||||||||
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
x |
|
7. |
ɉɨɞɫɱɢɬɚɣɬɟ ɨɩɪɟɞɟɥɟɧɧɵɣ ɢɧɬɟɝɪɚɥ ɨɬ ɮɭɧɤɰɢɢ f (x) = ln(x) ɧɚ ɩɪɨɦɟɠɭɬɤɟ [1, e]. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
´f |
1 |
|
|
|
|
|
|
|
|
|
|
8. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ µ |
|
|
dx . |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
µ |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
´2 |
|
|
1 |
|
|
|
|
|
|
|
|
9. |
ɉɨɞɫɱɢɬɚɣɬɟ ɧɟɫɨɛɫɬɜɟɧɧɵɣ ɢɧɬɟɝɪɚɥ |
µ |
|
|
dx . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
µ |
7 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ 2 |
|
|
|
|
|
|
|
|
|
|
|
10. ȼɵɱɢɫɥɢɬɟ ɩɥɨɳɚɞɶ ɮɢɝɭɪɵ, ɨɝɪɚɧɢɱɟɧɧɨɣ ɥɢɧɢɹɦɢ:
y = x2 4 x
y = 4 x
