4. Порядок выполнения работы

Определить коэффициент вязкости глицерина при комнатной температуре, измерив время вытекания объемачерез капилляр вискозиметра.

Получить температурную зависимость , измерив время вытекания объема глицериначерез капилляр вискозиметра при различных температурах в интервале.

Построить зависимость и определить энергию активации перескока, частоту колебаний молекулы глицерина около положения равновесияи частоту скачков.

5. Для получения зачета необходимо:

Уметь отвечать на вопросы типа:

1) Как вязкость жидкости зависит от температуры;

2) В чем отличие механизмов вязкого течения жидкостей и газов.

Лабораторная работа № 5. Изопроцессы в газе. Измерение отношения

1. Цель работы

Познакомиться с методом Клемана-Дезорма определения . На примере этой работы практически познакомиться с некоторыми процессами в газе. Научиться графически изображать процессы в газе с соблюдением масштабов.

2. Вопросы, знание которых обязательно для допуска к выполнению

1) Что называется теплоемкостью системы?

2) Удельная теплоемкость вещества.

3) Изохронная, изобарная молярная теплоемкости газа и их связь.

4) Теоретическое значение для одноатомных и двухатомных газов.

5) Как связаны теплоемкость при постоянном объеме и внутренняя энергия газа?

6) Чему равна теплоемкость газа при постоянной температуре?

7) Изохорический, изотермический, изобарический процессы в газах. Их уравнения.

8) 1 начало термодинамики.

9) Адиабатический процесс в газе. Его уравнение.

10) Как изменяется температура тела при адиабатическом расширении, при адиабатическом сжатии? (уравнение адиабаты, связывающее температуру и объем).

3. Сведения из теории

Теплоемкости различных веществ относятся к числу их важнейших термодинамических характеристик. В физике рассматриваются исходная и изобарнаятеплоемкости. Последняя сравнительно легко измеряется экспериментально, в то время как измеритьсложно. Значительно проще измерить. Измерениепредставляет интерес еще и потому, что само это отношение непосредственно входит во многие уравнения термодинамики.

Впервые величина для газов была измерена французскими физиками Клеманом и Дезормом в 1819г. Настоящая работа повторяет идею их опыта. Измерениепредлагаемым методом основано на том, что величинавходит в уравнение адиабаты идеального газа

(уравнение Пуассона)

чтобы определить , достаточно провести адиабатный процесс в изучаемом газе, измерить параметры двух разных состояний, а затем из уравнения

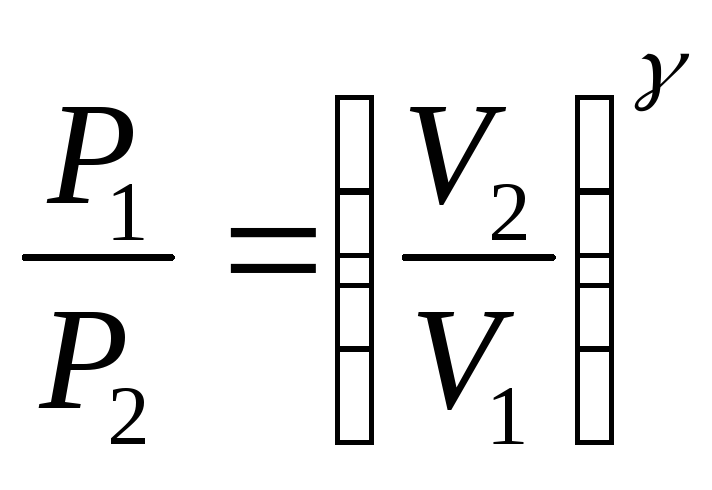Найти величину .

Однако, измерить , объемы занимаемые моле газа в двух различных состояниях практически невозможно.

В методе Клемана-Дезорма эта трудность преодолена путем проведения двух изопроцессов – адиабатного расширения газа и изохорного нагрева.

4. Порядок выполнения работы

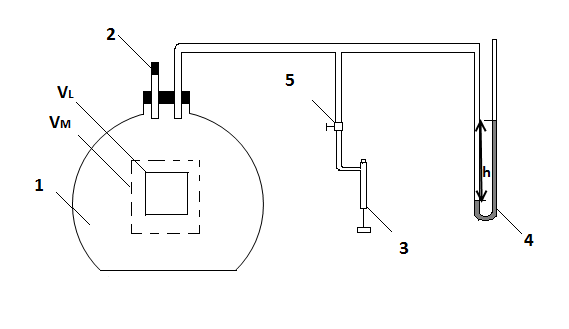
Рис.1

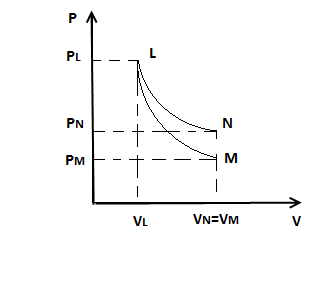
Рис.2

Экспериментальная установка для определения воздуха изображена на рис. 1. она состоит из бутыли большого объема, закрытой пробкойи соединенной с насосоми жидкостным манометром.

С помощью насоса накачать в бутыльпри закрытой пробкенекоторое дополнительное количество газа. Давление газа в бутыли станет больше атмосферного на. При накачивании газа совершается работа против сил давления газа, что приводит к увеличению его внутренней энергии, а следовательно и температуры. Процесс остывания газа до комнатной температуры путем теплообмена через стенки бутыли происходит при постоянном объемеи сопровождается понижением давления. Установившееся в результате релаксации температуры состояниехарактеризуется параметрами:

; ;

Где – объем моля газа, выделенный сплошной рамкой на рис. 1.

Открыть пробку в бутыли. Процесс выравнивания давлений займет 1-2секунды и, следовательно, процесс с достаточной точностью можно считать адиабатным.

После выравнивания давлений быстро закрыть пробку.

Газ в бутыли перейдет в состояние , которое характеризуется параметрами:

; ;

При адиабатном расширении произойдет некоторое охлаждение газа в бутили. После релаксации температуры газа в бутили к комнатной при изохорном процессе становится состояние , характеризующееся параметрамии. Так как в состояниях, можно сказать, что в координатахточки, характеризующие эти состояния, лежат на одной изотерме.

Из уравнения адиабатного процесса следует, что

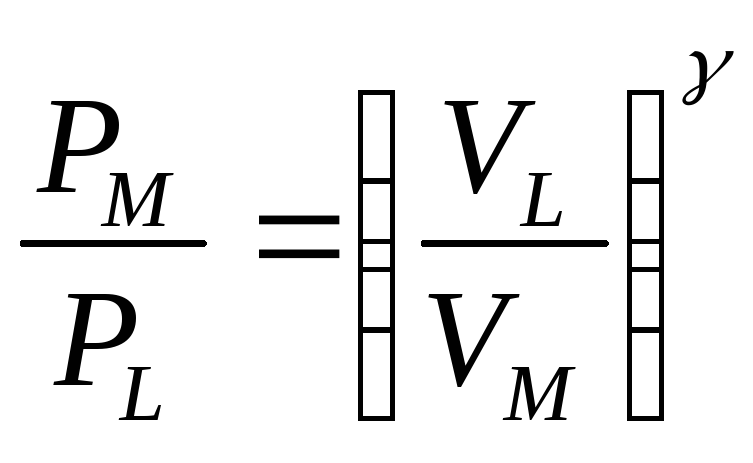
Из условий изотермического процесса находим, что

.

Из условий изохорного процесса следует, что

.

Из этих трех соотношений получаем:

.

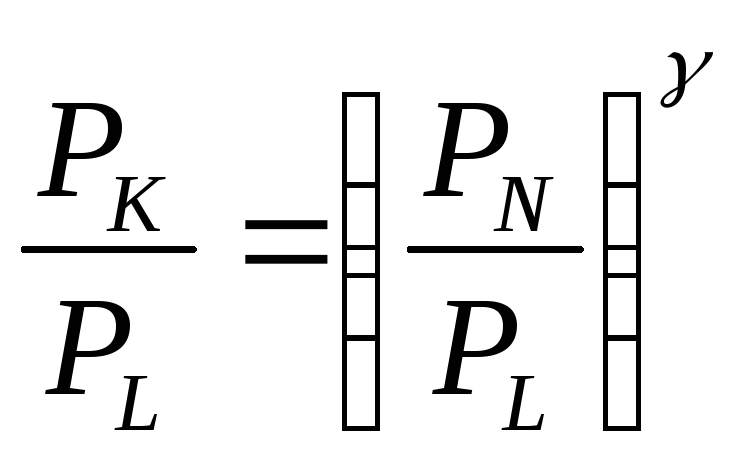Так как ;

вытекает 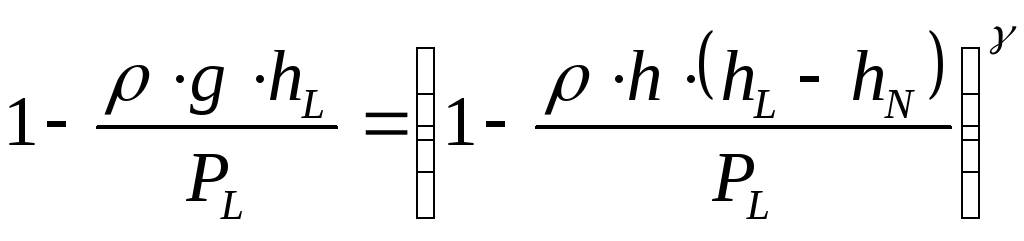откуда

,

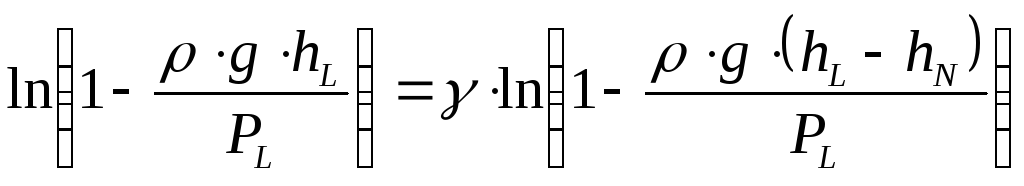Т.к. , то из условия, что приполучим:

или .

Таким образом, чтобы вычислить , необходимо измерить разность высот столбов жидкости в манометре в состоянии.

Из молекулярно-кинетической теории газов известно, что , а, следовательно, где– число степеней свободы молекулы. Зная, можно определить число степеней свободы молекул газа и оценить степень достоверности экспериментальных результатов.