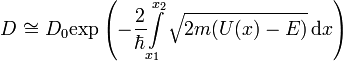[Править] Получение уравнения Шрёдингера предельным переходом[источник не указан 32 дня]

Существует способ ^{[источник не указан 32 дня]}получить уравнение Шрёдингера, используя предельный переход к классической механике.

Рассмотрим оператор

Поскольку интеграл , взятый по всему пространству, есть величина постоянная (для нормированной функции равная 1) то:

(Звездочкой будем обозначать комплексное сопряжение) Подставляя сюда наш оператор (оператор со звездочкой — комплексно сопряженный, с тильдой — транспонированный):

Иначе:

Поскольку это равенство должно выполняться для произвольной функции , то отсюда следует, что тождественно, то есть операторэрмитов. Чтобы выяснить смысл этого оператора, подействуем им на функцию(функция квазиклассической системы,— медленно меняющаяся функция,-действие):

Пренебрегая первым членом в силу его малости получаем:

То есть — собственное значение нашего оператора. Но эта производная есть не что иное, как классическая энергия системы (функция Гамильтона). Поэтому этот оператор называют гамильтонианом или гамильтоновым оператором.

Мы не будем здесь приводить вывод оператора импульса (точнее, оператора величины, сохраняющейся в силу однородности пространства), приведем лишь результат:

Или в компонентах (оси …):

В том, что это есть оператор величины переходящей в классический импульс можно убедиться, тем же методом, что был предложен для гамильтониана. Можно показать, что сохраняющаяся со временем величина, в частности импульс, измерима одновременно с энергией. Поэтому мы предположим, что соотношение между операторами импульса и энергии совпадает с классическим соотношением между соответствующими величинами:

Но:

Таким образом:

Тунне́льный эффект,туннели́рование— преодолениемикрочастицейпотенциального барьерав случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительноквантовойприроды, невозможное и даже полностью противоречащееклассической механике. Аналогом туннельного эффекта вволновой оптикеможет служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрениягеометрической оптики, происходитполное внутреннее отражение. Явление туннелирования лежит в основе многих важных процессов ватомнойимолекулярнойфизике, в физикеатомного ядра,твёрдого телаи т. д.

Отражениеи туннелирование электронного пучка, направленного напотенциальный барьер. Слабое пятно справа от барьера — электроны, прошедшие сквозь барьер. Обратите внимание наинтерференциюмежду падающими и отражающимися волнами.

Содержание  [убрать] 1 Краткое квантовомеханическое описание 2 Упрощённое объяснение 3 Макроскопические проявления туннельного эффекта 4 См. также 5 История и исследователи 6 Примечания 7 Ссылки 8 Литература

[Править] Краткое квантовомеханическое описание

Согласно классической механике, частица может находиться лишь в тех точках пространства, в которых её потенциальная энергия — Upot, меньше полной. Это следует из того обстоятельства, что кинетическая энергия частицыне может (в классич. физике) быть отрицательной, так как в таком случае импульс будетмнимой величиной. То есть, если две области пространства разделены потенциальным барьером, таким, что, просачивание частицы сквозь него в рамках классической теории оказывается невозможным. В квантовой же механике, мнимое значение импульса частицы соответствует экспоненциальной зависимости волновой функции от её координаты. Это показываетуравнение Шрёдингерас постоянным потенциалом:

(упрощенное уравнение Шрёдингера в одномерном случае) где координата;полная энергия,потенциальная энергия,редуцированная постоянная Планка,массачастицы).

Если , то решением этого уравнения является функция:

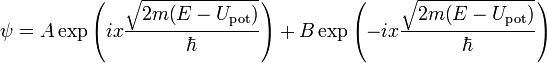
Пусть имеется движущаяся частица, на пути которой встречается потенциальный барьер высотой, а потенциал частицы до и после барьера. Пусть так же начало барьера совпадает с началом координат, а его «ширина» равна.

Для областей (до прохождения),(во время прохождения внутри потенциального барьера) и(после прохождения барьера).получаются соответственно функции:

где ,

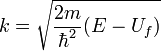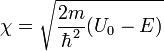
Так как слагаемое характеризует отраженную волну, идущую из бесконечности, которая в данном случае отсутствует, нужно положить. Для характеристики величины туннельного эффекта вводится коэффициент прозрачности барьера, равный модулю отношения плотности потока прошедших частиц к плотности потока упавших:

Для определения потока частиц используется следующая формула:

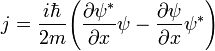
где знак *обозначаеткомплексное сопряжение.

Подставляя в эту формулу волновые функции, указанные выше, получим

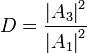
Теперь, воспользовавшись граничными условиями, выразим сначала ичерез(с учетом, что):

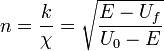
а затем через:

Введем величину

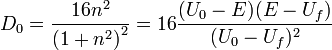
которая будет порядка единицы. Тогда:

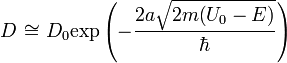
Для потенциального барьера произвольной формы делаем замену

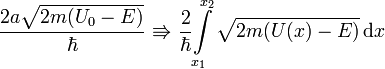
где инаходятся из условия

Тогда для коэффициента прохождения через барьер получаем выражение