Задание 2. Проверка закона Ома для участка цепи.

1. В режиме постоянного тока измерить зависимость напряжения от тока в цепи для каждого из сопротивлений. Для этого переключатель«J–R_n» установить в положения – «1», «2», «3», и регулятором тока задавать различные значения силы тока, протекающего по цепи. Полученные данные записать в таблицу.

2. По результатам измерений построить графики зависимостей . Используя метод наименьших квадратов, рассчитать сопротивлениякак угловые коэффициенты построенных графиков по формуле (П7), где,,.

3. Рассчитать погрешность углового коэффициента по формуле (П8) представить результат измерения в виде, где.

4. Возможен и другой способ определения погрешности поi-му единичному измерению:

,

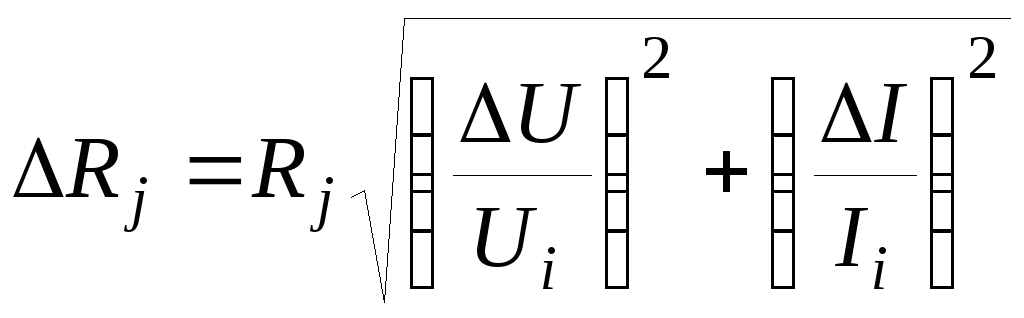где и– абсолютные погрешности измерительных приборов.

Задание 3. Проверка закона Ома для цепи переменного тока с индуктивностью.

1. Переключатель режимов перевести в режим переменного тока. Вращая ручку регулятора тока, снять зависимость напряжения от тока в цепи на каждой из катушек индуктивности . Выбор катушек провести с помощью программного переключателя. Полученные данные записать в таблицу.

2. По результатам измерений построить графики зависимостей . Используя метод наименьших квадратов, рассчитать полные сопротивления катушеккак угловые коэффициенты построенных графиков по формуле (П7), где,,.

3. Рассчитать погрешность углового коэффициента по формуле (П8), представить результат измерения в виде, где.

4. По формуле (3.24) рассчитать полные сопротивления катушек, подставив значения активных сопротивлений R, индуктивностей L и частоты переменного тока . Полученный результат сравнить с экспериментальным.

4. Магнитное поле

Цель работы: знакомство с основными характеристиками магнитного поля, определение напряженности магнитного поля короткого соленоида.

Основные теоретические сведения

Движущиеся заряды создают в пространстве вокруг себя магнитное поле, поэтому в пространстве, окружающем токи и постоянные магниты, существует магнитное поле.

Количественными характеристиками магнитного поля являются магнитная индукция и напряженность магнитного поля.

Элемент проводника с токомсоздает в точке, находящейся на расстоянииот него поле с индукцией, которая определяется законом Био-Савара-Лапласа:

. (4.1)

Рис. 4.1. Взаимная ориентация векторов,и

Направлениеперпендикулярнои, т.е. перпендикулярно плоскости, в которой лежат эти векторы, и определяется правилом правой тройки векторов: с конца результирующего векторавращение от первого векторако второмупроисходит против часовой стрелки.

Магнитное поле можно изобразить при помощи силовых линий – линий, касательные к которым в каждой точке совпадают с направлением вектора индукции магнитного поля. Силовые линии магнитного поля замкнуты.

Для магнитного поля справедлив принцип суперпозиции: магнитное поле, создаваемое несколькими токами, равно векторной сумме магнитных полей, создаваемых каждым током в отдельности.

Mагнитное поле проводника конечной длиныможет быть найдено путем интегрирования:, гдеопределяется законом Био-Савара-Лапласа, интегрирование производится по всей длине проводника.

Кроме вектора магнитной индукции в качестве характеристики поля используют напряженность магнитного поля . В однородной изотропной среде вектор индукции связан с вектором напряженности следующим соотношением:

. (4.2)

Здесь Гн/м – магнитная постоянная,– магнитная проницаемость среды.

Рис. 4.2 Катушка индуктивности

Получим формулу для магнитной индукции в центре короткого соленоида. Соленоид или катушка индуктивности представляет собой несколько последовательно соединенных одинаковых витков провода (рис. 4.2). Используем формулу для магнитной индукции вдоль оси кругового витка с током

, (4.3)

где I– сила тока, протекающего в витке,R – радиус витка,a – расстояние между центром витка и наблюдаемой точкой. Вектор магнитной индукции лежит вдоль оси симметрии витка. Согласно формуле (4.3) виток элементарной длины, являющейся частью катушки, создаёт в центре катушки магнитное поле величиной

, (4.4)

где x – координата выделенного витка,  – ток, протекающий по выделенному витку, N – количество витков в катушке, l – длина катушки.

Применим принцип суперпозиции, т.к. вектора для всех элементарных витков направлены в одну и ту же сторону, то принцип суперпозиции сводится к алгебраическому сложению:

. (4.5)

Из формулы (4.5) в случае среды со слабыми магнитными свойствами следует формула для напряжённости магнитного поля:

. (4.6)

Рис. 4.3 Круговая рамка с током и магнитная стрелка

Наличие магнитного поля можно обнаружить по его действию на внесенные в него проводники с током или постоянные магниты. В качестве последних можно использовать магнитную стрелку, изготовленную из намагниченной стальной пластинки, или рамку с током – замкнутый плоский контур произвольной формы, размеры которого малы по сравнению с расстоянием до токов, образующих поле. Каждый из этих физических объектов обладает собственным магнитным полем. Магнитные поля этих объектов по форме похожи, поэтому магнитную стрелку всегда можно представить в виде круговой рамки с током I(рис. 4.3).

Рис. 4.4 Круговая рамка с током во внешнем поле

В качестве характеристики магнитных свойств круговой рамки с током вводят физическую векторную величину – магнитный дипольный момент, гдеI– сила тока в рамке,– площадь поверхности, ограниченной рамкой,– вектор нормали, начало которого находится в центре рамки. Направление векторасовпадает с направлением вектора магнитной индукции собственного поля в центре рамки или с направлением северного полюса магнитной стрелки (рис. 4.4).

Если рамку с током поместить во внешнее однородное магнитное поле с индукцией , то на участки проводника начнут действовать силы Ампера, момент которых определяется по формуле

,, (4.7)

где – угол между векторамии.

Под действием момента амперовых сил рамка начнёт вращение, ориентируясь в положение, при котором момент сил становится равным нулю, т.е. при , когда.