
glossaryalggeom (1)
.docxГлоссарий по алгебре и геометрии
1) Подстановка-взаимно однозначное отображение ϕ множества X ={1,2…n} на себя.
2) Цикл длины m-Подстановка вида
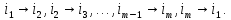
(При этом все числа i1, i2, …, im - различны).
3) Определителем или детерминантом n-го порядка называется число, полученное из элементов данной таблицы по следующим правилам:
1. Определитель n – го порядка равен алгебраической сумме n! членов.
2.Каждый член последовательности представляет собой произведение n – элементов, взятых по одному из каждой строки и каждого столбца таблицы.
3.
Член берется со знаком плюс, если
перестановки, образованные первыми и
вторыми индексами элементов
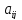 ,
входящие в произведение, одинаковой
четности(либо обе четные, либо нечётное)
и со знаком минус в противоположном
случае.
,
входящие в произведение, одинаковой
четности(либо обе четные, либо нечётное)
и со знаком минус в противоположном
случае.
4)
Минором
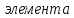
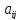 определителя n-го
порядка
называется определитель (n-1)
-ого порядка полученный из А вычеркиванием
i-й
строки и j-го
столбца, на пересечении которых стоит
данный элемент
определителя n-го
порядка
называется определитель (n-1)
-ого порядка полученный из А вычеркиванием
i-й
строки и j-го
столбца, на пересечении которых стоит
данный элемент
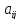 .
.
5)
Алгебраическим
дополнением
элемента
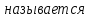 число
число
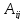 =
=
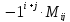 .
.
6) Матрицей называется таблица чисел вида
А=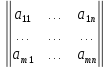 =
=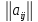 ,
,
сoстоящая из m строк и n столбцов..
7) Рангом матрицы А называется наибольшее натуральное число k для которого существует не равный нулю определитель k-го порядка, порожденный матрицей А.
8) Высказыванием называется всякое суждение, о котором можно сказать истинно оно или ложно.
9) Элементарная сумма – формула, представляющая собой дизъюнкцию высказываний и их отрицаний.
10) Элементарное произведение – формула, представляющая конъюнкцию высказываний и их отрицаний.
11) Дизъюнктивная нормальная форма(ДНФ) – дизъюнкция элементарных произведений.
12) Конъюнктивная нормальная форма(КНФ) – произведение элементарных сумм.
13) Совершенная дизъюнктивная форма – особая дизъюнктивная нормальная форма, в которой в каждое произведение входят все переменные либо непосредственно, либо с отрицанием.
14)
Наибольшим общим делителем отличным
от нуля многочленов
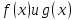 называется такой многочлен
называется такой многочлен
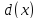 ,
который является их общим делителем и,
вместе с тем, сам делится на любой другой
общий делитель этих многочленов.
,
который является их общим делителем и,
вместе с тем, сам делится на любой другой
общий делитель этих многочленов.
15) Многочлены называются тождественно равными, если при всех значениях переменной их значения совпадают.
16) Конечное множество – это такое множество, для которого существует натуральное число, являющееся числом его элементов.
17)
Счетное
множество
– это такое множество, элементы которого
можно занумеровать в бесконечную
последовательность:
 .
.
18) Равночисленными множествами называют два конечных множества А и В, которые имеют одинаковое количество элементов.
19) Между элементами множеств А и В установлено взаимно однозначное соответствие, если каждому элементу множества А можно по некоторому правилу поставить в соответствие один и только один элемент множества В и, наоборот, каждому элементу множества В по некоторому правилу можно поставить в соответствие один и только один элемент множества А.
20) Декартово произведение множеств - множество всех упорядоченных пар (a, b), где a ϵ A, b ϵ B, где A и B - данные множества.
21) Отношение множеств A и B – подмножество R декартова произведения A×B.
22) Бинарным отношением между двумя множествами называется соответствие элементов одного из них элементам второго.
23) Полным порядок на M называется отношение R, если оно антисимметричное, транзитивное и полное.
24) Графом Г называется непустое множество M и множество отношений, заданных на M.Обозначается Г= (M, Q), Q-множество отношений, заданных на M.
25) Отображением f множества X в множество Y называется такое соответствие, при котором каждому элементу x множества X соответствует единственный элемент y, принадлежащий Y.
26) Обратимое (взаимно однозначное) отображение множества X на Y-отображение f множества X на множество Y, при котором каждый элемент y множества Y является образом точно одного элемента x множества X.
27) Преобразование множества-обратимое отображение множества на себя.
28) Сюръекция-отображение множества A на множество B.
29) Биекция-обратимое отображение.
30) Инъекция-отображение X в множество Y такое, что каждый элемент из Y является образом не более одного элемента из X.
31) Числовая функция-правило, по которому каждому x ϵ X поставлено в соответствие единственное число y.
32) Кольцом называют непустую систему множеств R, замкнутую относительно пересечения и симметрической разности конечного числа элементов.
33) Приведенной системой вычетов по этому модулю m называют совокупность чисел, взятых из полной системы вычетов и взаимно простых с модулем m.
34) Полной системой вычетов по модулю m называется совокупность m целых чисел, содержащая точно по одному представителю из каждого класса вычетов по модулю m.
35)
Функция
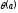 называется мультипликативной,
если выполнены следующие условия:
называется мультипликативной,
если выполнены следующие условия:
1.
Функция
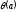 определена для всех целых положительных
a
и не обращается в нуль хотя бы при одном
таком a;
определена для всех целых положительных
a
и не обращается в нуль хотя бы при одном
таком a;
2.
Для любых положительных взаимно простых
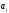 и
и
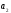 имеем
имеем
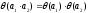 .
.
36)
Равноостаточными(или
сравнимыми) между
собой по модулю m
называют два целых числа a
и b,
дающих при делении на натуральное число
m
один и тот же остаток:
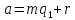 ,
,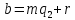 ,
0≤r<m
называются. Обозначение:
,
0≤r<m
называются. Обозначение:
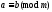 читается: a
сравнимо с b
по модулю m.
читается: a
сравнимо с b
по модулю m.
37) Линейным порядком на множестве А называется отношение частичного порядка, при котором из любой пары элементов можно выделить предшествующий и последующий.
38) Частичный порядок – это рефлексивное, транзитивное, несимметричное отношение R на множестве A.
39) Линейным пространством над полем действительных чисел называется множество, над которым определены операции сложения и умножения на произвольное действительное число.
40)
Кортежем длины n,
составленным из элементов множеств
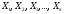 ,
называется конечная последовательность
,
называется конечная последовательность
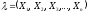 ,
где для всех k
(
,
где для всех k
(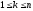 )
имеем
)
имеем
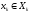 .
Элемент
.
Элемент
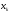 называется k-ой
координатой (или k-ой
координатой) кортежа
называется k-ой
координатой (или k-ой
координатой) кортежа
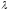 .
.
41) Размещениями с повторениями из m элементов по k называют кортежами длины k составленные из элементов m – элементного множества X.
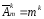 .
.
42)
Размещениями без повторений
из m
элементов множества X
по k
называют упорядоченное множество длины
k
составленное из элементов m
– элементарного множества X
и обозначают
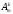 .
.
Число размещений без повторений из m элементов по k находится по формуле:
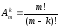 .
.
43)
Перестановками
без повторений из m
элементов
называют размещения без повторений из
этих элементов по m.
Число перестановок из m
элементов обозначают
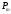 и
находятся по формуле:
и
находятся по формуле:
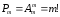 .
.
44)
Сочетаниями без повторений из элементов
этого множества по k
называют k
– элементные подмножества m
– элементного множества X.
Их число обозначают
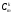 и обозначают:
и обозначают:
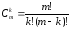 .
.
45)
Перестановкой
с повторениями
состава
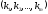 из букв
из букв
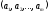 называют любой кортеж длины
называют любой кортеж длины
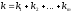 ,
в который буква
,
в который буква
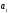 входит
входит
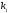 раз, …, а буква
раз, …, а буква
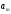 входит
входит
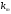 раз. Число таких перестановок обозначают
раз. Число таких перестановок обозначают
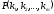 .
.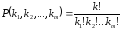 .
.
46)
Сочетаниями
с повторениями из m
элементов по k
- набор,
состоящий из k
– элементов и предметов m
видов.
Число сочетаний с повторениями из m
элементов по k
обозначим
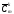 :
:
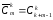 .
.
47) Базисный минор - минор, не равный нулю, а окаймляющие его миноры либо все равны 0, либо отсутствуют.
48) Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.
49) Линейный порядок на множестве А – отношение частичного порядка, при котором из любой пары можно выделить предшествующий и последующий.
50) Комплексное число z – выражение вида z=x+iy-алгебраическая форма комплексного числа .
51)
Проекция
вектора
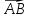 на
ось
на
ось
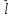 это число, равное длине вектора
это число, равное длине вектора
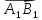 , взятое со знаком «+», если направление
, взятое со знаком «+», если направление
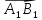 совпадает с направлением
совпадает с направлением
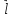 и со «-», если направление
и со «-», если направление
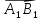 не совпадает с направлением
не совпадает с направлением
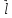 .
.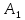 – проекция
– проекция
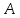 на ось
на ось
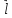 ,
,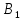 -проекция
-проекция
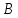 на ось
на ось
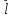 .
.
52)
Полярная
система координат на плоскости
— это совокупность точки ![]() ,
называемой полюсом,
и полупрямой
,
называемой полюсом,
и полупрямой ![]() ,
называемой полярной
осью.
,
называемой полярной
осью.
53) Полярными координатами произвольной точки M (относительно заданной системы) называются ρ = OP и θ = ‹NOP (рисунок 7). Угол θ при этом следует понимать так, как принято в тригонометрии. Число ρ называется полярным радиусом, число θ – полярным углом точки M.
54) Упорядоченная тройка некомпланарных векторов а1, а2, а3 называется правой, если наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от а1 ка2 и от а2 к а3 кажутся происходящими против часовой стрелки. Если повороты происходят по часовой стрелке, то тройка – левая.
55) Аффинными координатами любой точки М называются координаты вектора, определяемые относительно базиса.
56) Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, величина постоянная.
57)
Эксцентриситетом
эллипса называется отношение
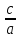 ,
где с- половина расстояния между
фокусами, a
– большая полуось эллипса.
,
где с- половина расстояния между
фокусами, a
– большая полуось эллипса.
58)
Директрисами
эллипса
называются две прямые, перпендикулярные
большой оси эллипса и расположенные
симметрично относительно центра на
расстоянии
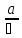 от него.
от него.
59) Гипербола - множество точек M плоскости, для каждой из которых модуль разности расстояний от точек F1 и F2 равен 2a, Точки F1 и F2 называются фокусами гиперболы; 2a - действительная ось.
60) Параболой называется геометрическое место точек на плоскости, расстояние которых до некоторой точки, называемой фокусом и до некоторой прямой, называемой директрисой, не проходящей через фокус, равны.
61) Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
62) Поверхность второго порядка – поверхность, которая в прямоугольной системе координат определяется алгебраическим уравнением второй степени.
63)
Конусом
второго
порядка называется поверхность, которая
в некоторой декартовой системе координат
определяется уравнением:
![]()
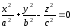 .
.
64)
Эллипсоидом
называется
поверхность, которая в некоторой
декартовой системе координат определяется
уравнением:
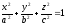 .
.
65)
Однополостным
гиперболоидом
называется поверхность, которая в
некоторой декартовой системе координат
определяется уравнением:
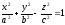 .
.
66)
Двуполостным
гиперболоидом
называется поверхность, которая в
некоторой декартовой прямоугольной
системе координат определяется
уравнением:
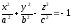 .
.
67)
Эллиптическим
параболоидом
называется поверхность, которая в
некоторой декартовой прямоугольной
системе координат задается уравнением:
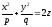 ,
где
p>0,
q>0.
,
где
p>0,
q>0.
68)
Гиперболическим
гиперболоидом называется
поверхность, которая в декартовой
прямоугольной системе координат задается
уравнением
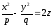 ,
где p>0,
q>0.
,
где p>0,
q>0.
69)
Алгебраической
операцией,
определенной в М будем называть функцию
f,
которая каждой упорядоченной паре
элементов a,b M
ставим в соответствие некоторый
определенный элемент c
M
ставим в соответствие некоторый
определенный элемент c
 М.
М.
70) Группоидом называется множество с одной алгебраической операцией, на которую не налагается никаких условий.
71) Полугруппами называются группоиды с ассоциативной операцией.
72) Группа – это множество замкнутое относительно одной ассоциативной алгебраической операции, содержащее единичный элемент и такой, что для каждого ее элемента а существует обратный элемент, который удовлетворяет равенству.
73) Абелевой группой называется группа, в которой умножение коммутативно.
74) Конечная группа – группа, состоящая из конечного числа элементов, число ее элементов называется порядком группы.
75) Симметрической группой n-й степени называется группа всех подстановок множества, состоящего из n элементов.
76)
Изоморфными
группами G
и G'
называют группы,
между элементами которых можно установить
такое взаимно однозначное соответствие,
так, что если а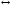 а'
и b
а'
и b
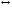 b',
где а, b
b',
где а, b
 G
,
G
, а'
,b'
а'
,b' G',
то ab
G',
то ab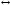 а'
b'.
а'
b'.
77)
Автоморфизмом
группы G
называют
изоморфное отображение φ: G
 G
группы G
на себя ,положив, G'=
G
в определении изоморфизмами.
G
группы G
на себя ,положив, G'=
G
в определении изоморфизмами.
78)
Гомоморфизмом
называется
отображение f::
G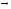 G'
группы (G,
G'
группы (G, )
в (G',
)
в (G', ),
если
),
если
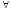 а,b
а,b G
f
(a
G
f
(a
 b)=f(a)
b)=f(a)
 f(b).
f(b).
79)
Кольцом
называется (К,+, ),если
К – не пустое множество, на котором
заданы две бинарные алгебраические
операции «+» (сложение) и «
),если
К – не пустое множество, на котором
заданы две бинарные алгебраические
операции «+» (сложение) и « »
(умножение), удовлетворяющие следующим
условиям:
»
(умножение), удовлетворяющие следующим
условиям:
1). (К, +) – абелева группа;
2).
(К, )
– полугруппа;
)
– полугруппа;
3).
операции (+) и ( )
связаны дистрибутивными законами
(другими словами, умножение дистрибутивно
по сложению).
)
связаны дистрибутивными законами
(другими словами, умножение дистрибутивно
по сложению).
(a+b)c=ac+bc,
c(a+b)=ca+cb
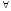 a,b,c
a,b,c К.
К.
80)
Подкольцом
называется
подмножество L кольца К, если х,у L
L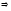 х-у
х-у L,
ху
L,
ху L,
то есть если L подгруппа аддитивной
группы и подполугруппа мультипликативной
полугруппы кольца.
L,
то есть если L подгруппа аддитивной
группы и подполугруппа мультипликативной
полугруппы кольца.
81)
Поле
Р –
это коммутативное кольцо с единицей
(1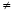 0)
в котором каждый элемент обратим а
0)
в котором каждый элемент обратим а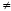 0.
0.
82) Простое поле – поле, не обладающее никаким собственным подполем.
83) Отношением эквивалентности (эквивалентностью) называют отношение Р, если Р рефлексивно, симметрично и транзитивно.
Обозначение Е или ~ (тильда).
84)
Линейной
функцией
называется функция
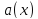 , если:
a)
, если:
a)
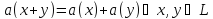 (условие аддитивности).
б)
(условие аддитивности).
б)
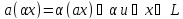 (условие однородности).
(условие однородности).
85)
Билинейной
функцией называется
числовая функция
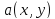 двух
векторных аргументов
двух
векторных аргументов
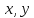 ,
если она линейна по каждому аргументу.
То есть:
,
если она линейна по каждому аргументу.
То есть:
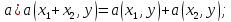

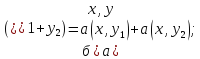
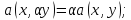
Здесь
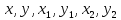 –
любые векторы пространства
–
любые векторы пространства
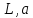 – произвольное число.
– произвольное число.
86)
Положительно
(отрицательно) определённой
квадратичной
формой называется квадратичная форма
A,
определённая в действительном линейном
пространстве
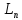 ,
если:
,
если:
∀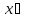
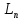 ,
,
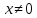
A > 0 (A <0).
87) Нормальным видом квадратичной формы называется сумма квадратов нескольких неизвестных с коэффициентами +1 или -1.
88)
Ортогональной
квадратичной матрицей
называется квадратичная матрица
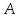 ,
если
ее элементы действительны и выполняется
одно из пяти следующих эквивалентных
свойств:
,
если
ее элементы действительны и выполняется
одно из пяти следующих эквивалентных
свойств:
-
Строки образуют ортонормированную систему;
-
Столбцы образуют ортонормированную систему;
-
 ;
; -
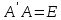 ;
; -
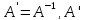 – транспонированная
матрица для
– транспонированная
матрица для
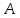 .
.
89) Сигнатурой формы f называется разность между положительным и отрицательным индексами инерции.
90) Положительным(отрицательным) индексом инерции формы f называется число положительных (отрицательных)квадратов в той нормальной форме, к которой приводится данная действительная квадратичная форма.
91)
Скалярным
произведением называют
отображение
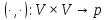 ,
где V
– вещественное или комплексное линейное
пространство, удовлетворяющее следующим
аксиомам :
,
где V
– вещественное или комплексное линейное
пространство, удовлетворяющее следующим
аксиомам :
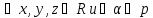 ;
;
-
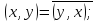
-
(
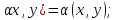
-
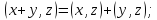
-
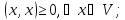
-
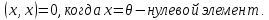
92) Евклидовым пространством E называют вещественное, линейное пространство со скалярным произведением.
93) Унитарным пространством V называют комплексное, линейное пространство со скалярным произведением.
94) Изоморфными линейными пространствами называют два линейных пространства V и U, если между их элементами можно установить такое взаимно однозначное соответствие, выполняемое условием:
Сумме векторов линейного пространства U соответствует сумма соответствующих векторов линейного пространства V.
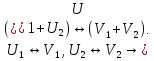
95)
Изоморфными
линейными евклидовами пространствами
называют
линейные евклидова пространства
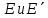 ,
если между их векторами можно установить
такое взаимно однозначное соответствие,
такое, что выполняется следующее
требование:
,
если между их векторами можно установить
такое взаимно однозначное соответствие,
такое, что выполняется следующее
требование:
1)
Это соответствие является изоморфным
соответствием между
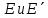 ,
которые в свою очередь рассматриваются
как линейные пространства.
,
которые в свою очередь рассматриваются
как линейные пространства.
2)
При этом соответствии сохраняется
скалярное произведение, то есть, если
образами
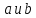 из Е служат соответственно
из Е служат соответственно
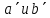 из
Е΄, то
из
Е΄, то
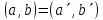 .
.
96) Верхней границей действительных корней многочлена называют число K, если он не имеет действительных корней больших или равных K.
97)
Интерполирующей
или интерполяционной функцией для
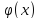 на отрезке [a,b]
называется функция f(x),
если ее значения
на отрезке [a,b]
называется функция f(x),
если ее значения
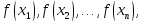 в заданных точках
в заданных точках
 ,
называемых узлами интерполяции, совпадают
с заданными значениями функции φ(x),
то есть с
,
называемых узлами интерполяции, совпадают
с заданными значениями функции φ(x),
то есть с
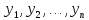 соответственно.
соответственно.
98) Симметрическим многочленом называют многочлен от x и y, если он не изменяется при замене x на y, а y на x.
99)
Элементарными
симметрическими многочленами от x
и y
называют симметрические многочлены
x+y
и xy.
Обозначают:
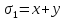 и
и
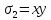 .
.
100)
Матричным
многочленом
называется выражение вида
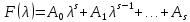 ,
где 𝛌
– переменная, а
,
где 𝛌
– переменная, а
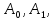 …,
…,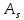 -
квадратные коэффициенты матрицы с
числовыми коэффициентами.
-
квадратные коэффициенты матрицы с
числовыми коэффициентами.
101)
Метрическим пространством
называется множество
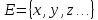 ,
если определено отображение
,
если определено отображение
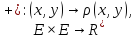 которое
для
которое
для
 ставит
в соответствие число 𝛒
,удовлетворяющее следующим аксиомам:
ставит
в соответствие число 𝛒
,удовлетворяющее следующим аксиомам:
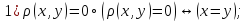
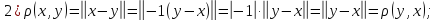
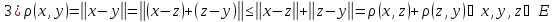
102)
Аннулирующим
многочленом для
квадратной матрицы A
порядка n
называется многочлен
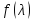 с числовыми коэффициентами, для которого
с числовыми коэффициентами, для которого
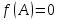 .
.
103) Минимальным многочленом квадратной матрицы A порядка n называется отличный от нуля аннулирующий многочлен для матрицы A минимальной степени, взятой со старшим коэффициентом равным 1.
104)
Нормой
в векторном пространстве E
называется отображение
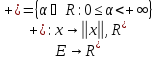 ,
удовлетворяющее следующим аксиомам:
,
удовлетворяющее следующим аксиомам:
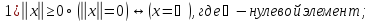
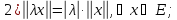
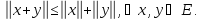
105) Преобразование множества – это биективное отображение множества на себя.
