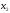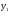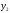Многочлены от одной переменной
.docx
Лекция №6
Многочлены от одной переменной
Выражение
вида ![]() ,
где
,
где ![]() —
некоторые числа и
—
некоторые числа и ![]() ,
называется многочленом
степени
,
называется многочленом
степени ![]() от
от ![]() .
.
Два
многочлена называются тождественно
равными,
если их числовые значения совпадают
при всех значениях ![]() .
Многочлены
.
Многочлены ![]() и
и ![]() тождественно
равны тогда и только тогда, когда они
совпадают, т.е. коэффициенты при одинаковых
степенях
тождественно
равны тогда и только тогда, когда они
совпадают, т.е. коэффициенты при одинаковых
степенях ![]() этих
многочленов одинаковы.
этих
многочленов одинаковы.
Операции над многочленами:
-
Сумма и разность многочленов:
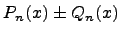 .
.
Суммой
и разностью многочленов ![]() и
и ![]() называется
следующий многочлен:
называется
следующий многочлен:
![]()
![]()
Степень
полученного многочлена ![]() не
превосходит максимальной степени
многочленов
не
превосходит максимальной степени
многочленов ![]() и
и ![]() .
.
-
Умножение на одночлен:
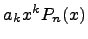 .
.
Умножим
одночлен ![]() на
многочлен
на
многочлен ![]() :
:
![]()
![]()
т.е. каждый член многочлена умножается на одночлен. Здесь применяем правило работы со степенями.
-
Умножение многочленов:
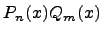 .
.
Умножим
многочлен ![]() на
на ![]() :
:
![]()
![]()
![]()
В
итоге свели операцию умножения многочленов
к умножению одночлена на многочлен.
Заметим, что при умножении многочленов
степени ![]() и
и ![]() получается
многочлен степени
получается
многочлен степени ![]() .
При умножении многочленов необходимо
каждый член одного многочлена умножить
на каждый член другого многочлена.
.
При умножении многочленов необходимо
каждый член одного многочлена умножить
на каждый член другого многочлена.
-
Деление многочленов:
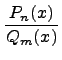 .
.
Разделим
многочлен ![]() на
на ![]() ,
то есть представим выражение
,
то есть представим выражение 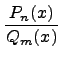 в
следующем виде:
в
следующем виде:
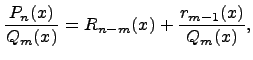
где ![]() -
частное от деления,
-
частное от деления, ![]() -
делимое,
-
делимое, ![]() -
делитель,
-
делитель, ![]() -
остаток.
-
остаток.
При
делении многочлена ![]() на
многочлен
на
многочлен ![]() ,
где
,
где ![]() ,
нужно найти многочлены
,
нужно найти многочлены ![]() и
и ![]() такие,
чтобы выполнялось равенство
такие,
чтобы выполнялось равенство
Теорема Безу
Теорема
Безу. Остаток
от деления многочлена ![]() на
двучлен
на
двучлен ![]() равен
значению этого многочлена при
равен
значению этого многочлена при ![]() .
.
Следствие 1:
![]() .
.
Таким
образом, число ![]() является
корнем многочлена
является
корнем многочлена ![]() тогда
и только тогда, когда многочлен
тогда
и только тогда, когда многочлен ![]() делится
на двучлен
делится
на двучлен ![]() без
остатка.
без
остатка.
Если
многочлен ![]() делится
без остатка на
делится
без остатка на ![]() ,
но не делится без остатка на
,
но не делится без остатка на ![]() ,
то число
,
то число ![]() называется корнем
кратности
называется корнем
кратности ![]() для
многочлена
для
многочлена ![]() .
.
Следствие
1. Многочлен ![]() степени
степени ![]() имеет
не более
имеет
не более ![]() корней.
корней.
Следствие
2. Если
многочлен ![]() степени
степени ![]() имеет
имеет ![]() корней
(среди которых могут быть равные), то он
представим в виде:
корней
(среди которых могут быть равные), то он
представим в виде:
![]()
Теорема Виета
Теорема
Виета. Если
многочлен ![]() степени
степени ![]() имеет
имеет ![]() различных
корней
различных
корней ![]() ,
то имеют место следующие соотношения:
,
то имеют место следующие соотношения:
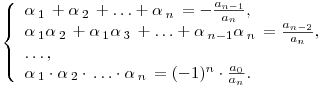
Замечание. Формулы Виета сохраняют силу и при наличии кратных корней, но в этом случае надо каждый корень учитывается столько раз, какова его кратность.
Наибольший общий делитель многочленов (НОД).
Наибольшим
общим делителем отличным от нуля
многочленов
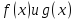 называется такой многочлен
называется такой многочлен
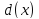 ,
который является их общим делителем и,
вместе с тем, сам делится на любой другой
общий делитель этих многочленов.
Обозначается НОД многочленов
,
который является их общим делителем и,
вместе с тем, сам делится на любой другой
общий делитель этих многочленов.
Обозначается НОД многочленов
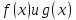 символом
символом
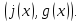
Для
нахождения НОД многочленов применяется
алгоритм Евклида, который состоит в
следующем. Пусть даны многочлены
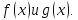 Делим
Делим
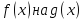 и получаем некоторый остаток
и получаем некоторый остаток
 .
Делим затем
.
Делим затем
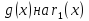 и получаем остаток
и получаем остаток
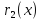 ,
делим
,
делим
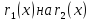 и так далее. В этой цепочке мы должны
дойти до такого места, на котором деление
совершится нацело и поэтому процесс
остановится. Тот
остаток
и так далее. В этой цепочке мы должны
дойти до такого места, на котором деление
совершится нацело и поэтому процесс
остановится. Тот
остаток
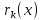 ,
на который нацело делится предыдущий
остаток
,
на который нацело делится предыдущий
остаток
 ,
и будет НОД многочленов
,
и будет НОД многочленов

Корни многочленов.
Если
 то есть многочлен
то есть многочлен
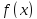 обращается в нуль при подстановке в
него числа
обращается в нуль при подстановке в
него числа
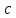 вместо
неизвестного, то
вместо
неизвестного, то
 называется
корнем многочлена
называется
корнем многочлена
 (или уравнения
(или уравнения
 ).
).
Если
мы будем делить многочлен
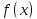 на произвольный многочлен первой
степени, то остаток будет либо некоторым
многочленом нулевой степени либо нулём,
то есть во всяком случае некоторым
числом
на произвольный многочлен первой
степени, то остаток будет либо некоторым
многочленом нулевой степени либо нулём,
то есть во всяком случае некоторым
числом
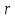 .
Следующая теорема
позволит найти остаток не прибегая к
самому делению многочлена, в случае,
когда производится деление на многочлен
вида
.
Следующая теорема
позволит найти остаток не прибегая к
самому делению многочлена, в случае,
когда производится деление на многочлен
вида
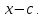 Остаток
от деления многочлена f(x)
на линейный многочлен
Остаток
от деления многочлена f(x)
на линейный многочлен
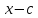 равен значению
равен значению
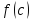 многочлена
многочлена
 при
при

Действительно, пусть

Беря
значения обеих частей этого равенства
при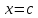 ,
мы получаем:
,
мы получаем:

что доказывает теорему.
Следствие:
Число
с тогда и только тогда будет корнем
многочлена
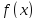 ,
если
,
если
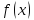 делится на
делится на
Кратные корни.
Если
в разложении многочлена ![]() -степени
-степени
![]() ,
,
некоторые множители окажутся одинаковыми, то
![]()
![]() ,
,
то ![]() -называется
корнем кратности
-называется
корнем кратности ![]() ,
, ![]() -кратности
-кратности ![]() и
т.д.
и
т.д.
Теорема
. Если а является корнем
многочлена ![]() кратности
кратности ![]() ,
то для производной
,
то для производной ![]() это
число является корнем кратности
это
число является корнем кратности ![]() .
.
Доказательство. Пусть
![]() ,
,
где ![]() не
обращается в 0 при
не
обращается в 0 при ![]() .
.
![]() ,
,
т.е. ![]() является
корнем кратности
является
корнем кратности![]() .
.
Следствие. Число а является
корнем кратности ![]() для
для ![]() ,…,
корнем кратности 1 для
,…,
корнем кратности 1 для ![]() .
.
Условия равенства двух многочленов
Определение. Многочлены называются тождественно равными, если при всех значениях переменной их значения совпадают.
Теорема 1. У равных многочленов равны коэффициенты при соответствующих степенях переменной.
Доказательство:
1.Если коэффициенты при соответствующих степенях переменной равны, то многочлены равны.
![]()
![]()
При любом значении х=с, значения многочленов равны. А(с) – В(с) = 0
2. Если многочлены равны, то и коэффициенты при соответствующих значениях х равны.
![]()
![]()
А(х)
= В(х)![]() А(х)
– В(х) = 0 при любом значении х=с.
А(х)
– В(х) = 0 при любом значении х=с.
Вычтем значения многочленов в столбик:
![]()
Но
сумма может быть равна 0 при любом с
только если значения всех выражений в
скобках равно 0, значит ![]() ;
; ![]() ;
; ![]() ;
…
;
… ![]()
Границы корней многочленов
Для
многочлена ![]()
1)
верхняя граница модулей корней -
число ![]() где
где ![]()
2)
верхняя граница положительных корней
- число ![]() где
где ![]() B -
наибольшее число из модулей отрицательных
коэффициентов; k -
номер первого из отрицательных
коэффициентов;
B -
наибольшее число из модулей отрицательных
коэффициентов; k -
номер первого из отрицательных
коэффициентов;
3)
нижняя граница положительных корней -
число ![]() где
где ![]() -
верхняя граница положительных корней
многочлена
-
верхняя граница положительных корней
многочлена ![]()
4)
верхняя граница отрицательных корней
- число -![]() где
где ![]() -
верхняя граница положительных корней
многочлена
-
верхняя граница положительных корней
многочлена ![]()
5)
нижняя граница отрицательных корней -
число -![]() где
где ![]() -
верхняя граница положительных корней
многочлена
-
верхняя граница положительных корней
многочлена ![]()
Схема Горнера
Схема
Горнера - один из простейших способов
деления многочлена ![]() на
бином x-a. Конечно, делением применение
схемы Горнера не исчерпывается, но для
начала рассмотрим именно это. Применение
алгоритма поясним на примерах.
Разделим
на
бином x-a. Конечно, делением применение
схемы Горнера не исчерпывается, но для
начала рассмотрим именно это. Применение
алгоритма поясним на примерах.
Разделим ![]() на
на ![]() .
Составим таблицу из двух строк: в первой
строке запишем коэффициенты многочлена
.
Составим таблицу из двух строк: в первой
строке запишем коэффициенты многочлена ![]() по
убыванию степеней переменной. Заметьте,
что данный многочлен не содержит х, т.е.
коэффициент перед х равен 0. Так как мы
делим на
по
убыванию степеней переменной. Заметьте,
что данный многочлен не содержит х, т.е.
коэффициент перед х равен 0. Так как мы
делим на ![]() ,
во второй строке запишем единицу:
,
во второй строке запишем единицу:
![]()
Начнем заполнять пустые ячейки во второй строке. В первую пустую ячейку запишем 5, просто перенеся ее из соответствующей ячейки первой строки:
![]()
Следующую
ячейку заполним по такому принципу: ![]()
![]()
Аналогично
заполним и четвертую: ![]() :
:
![]()
Для
пятой ячейки получим ![]() :
:
![]()
И,
наконец, для последней, шестой ячейки,
имеем ![]() :
:
![]()
Задача решена, осталось только записать ответ:

Как
видите, числа, расположенные во второй
строке (между первым и последним), есть
коэффициенты многочлена, полученного
после деления ![]() на
на ![]() .
Последнее число во второй строке означает
остаток от деления или, что то же самое,
значение многочлена
.
Последнее число во второй строке означает
остаток от деления или, что то же самое,
значение многочлена ![]() при
при ![]() .
Следовательно, если в нашем случае
остаток равен нулю, то многочлены делятся
нацело.
.
Следовательно, если в нашем случае
остаток равен нулю, то многочлены делятся
нацело.
![]()
Полученный
результат говорит также и о том, что 1
является корнем многочлена ![]() .
.
Приведем
еще один пример. Разделим многочлен ![]() на
на ![]() .
Сразу оговорим, что выражение
.
Сразу оговорим, что выражение ![]() нужно
представить в форме
нужно
представить в форме ![]() .
В схеме Горнера будет участвовать именно
-3.
.
В схеме Горнера будет участвовать именно
-3.
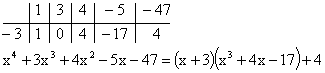
Если
наша цель - найти все корни многочлена,
то схему Горнера можно применять
несколько раз подряд, - до тех пор, пока
мы не исчерпаем все корни. Например,
отыщем все корни многочлена ![]() .
Целые корни нужно искать среди делителей
свободного члена, т.е. среди делителей
8. Т.е., целыми корнями могут быть числа
-8, -4, -2, -1, 1, 2, 4, 8. Проверим, к примеру, 1:
.
Целые корни нужно искать среди делителей
свободного члена, т.е. среди делителей
8. Т.е., целыми корнями могут быть числа
-8, -4, -2, -1, 1, 2, 4, 8. Проверим, к примеру, 1:
![]()
Итак, в остатке имеем 0, т.е. единица действительно является корнем данного многочлена. Попробуем проверить единицу еще несколько раз. Новую таблицу для этого создавать не будем, а продолжим использование предыдущей:
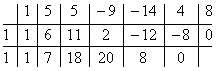
Вновь в остатке ноль. Продолжим таблицу до тех пор, пока не исчерпаем все возможные значения корней:
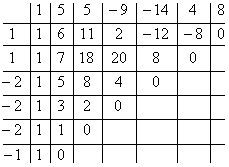
Итог: ![]() .
.
Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целых корней метод довольно-таки неплох.
Рациональные дроби
Рассмотрим
 , (1)
, (1)
где
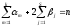 ,
,
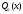 – многочлен n
– степени от x,
– многочлен n
– степени от x,
 – константа.
– константа.
Теорема (о разложении правильной рациональной дроби)
Если
 и
и
 – многочлены степени m
и n
соответственно, причем m<n
и коэффициенты этих многочленов
действительные числа, а
– многочлены степени m
и n
соответственно, причем m<n
и коэффициенты этих многочленов
действительные числа, а
 представляется в виде (1), то
представляется в виде (1), то
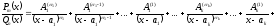
 . (2)
. (2)
Все коэффициенты разложения (2) являются действительными числами и определяются однозначно.
Пример 1.
Представить
рациональную дробь
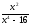 в виде простейших дробей над полем
вещественных чисел.
в виде простейших дробей над полем
вещественных чисел.
Решение.
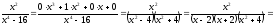

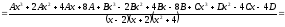
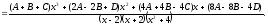
Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x.
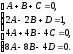
Решая
систему получим:
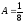 ,
,
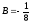 ,
,
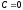 ,
,
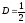 .
.
Имеем разложение
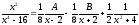 .
.
Пример для самостоятельного решения.
Представить
рациональную дробь
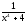 в виде суммы простейших дробей над полем
комплексных чисел.
в виде суммы простейших дробей над полем
комплексных чисел.
Указание.
Приравниваем
знаменатель к нулю
 ,
,
 ,
,
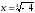 .
Извлекая корень, получим 4 корня
.
Извлекая корень, получим 4 корня
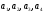 .
Представим
.
Представим
 .
Данная дробь будет иметь вид
.
Данная дробь будет иметь вид
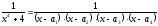 .
.
К последней дроби применяем теорему о разложении правильной рациональной дроби.
Разложение правильной рациональной дроби на простейшие, знаменатель которой разложен на попарно простые линейные множители.
Пусть дана правильная дробь
 ;
;
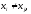 при
при
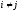 ,
i,j=1,2,…,n.
,
i,j=1,2,…,n.
В этом случае справедлива формула Лагранжа:
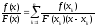 ,
,
где
 .
.
Интерполирование
Постановка задачи.
Пусть
в точках
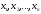 таких, что
таких, что
 .
Известны значения функции
.
Известны значения функции
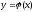 ,
то есть на отрезке [a,b]
задана табличная (сеточная) функция
,
то есть на отрезке [a,b]
задана табличная (сеточная) функция
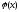 :
:
Таблица 1
|
x |
|
|
… |
|
|
y |
|
|
… |
|
Функция
f(x)
называется интерполирующей или
интерполяционной для
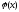 на отрезке [a,b],
если ее значения
на отрезке [a,b],
если ее значения
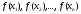 в заданных точках
в заданных точках
 ,
называемых узлами
интерполяции,
совпадают с заданными значениями функции
,
называемых узлами
интерполяции,
совпадают с заданными значениями функции
 ,
то есть с
,
то есть с
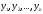 соответственно.
соответственно.
Будем
считать, что интерполяционная функция
f(x)
есть многочлен степени n-1,
тогда задача интерполяции формулируется
так: для функции
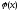 заданной таблицей 1 найти многочлен
заданной таблицей 1 найти многочлен
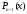 такой, чтобы выполнялась совокупность
условий интерполяции
такой, чтобы выполнялась совокупность
условий интерполяции
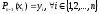 , (2)
, (2)
найти
многочлен
 это значит, учитывая его каноническую
форму
это значит, учитывая его каноническую
форму
 , (3)
, (3)
найти
его n
коэффициентов
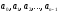 .
Обозначим через
.
Обозначим через
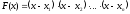 и рассмотрим рациональную дробь
и рассмотрим рациональную дробь
 .
Она правильная, так как степень многочлена
в числителе меньше степени многочлена
стоящего в знаменателе. Мы можем применить
формулу Лагранжа для разложения дроби
на простейшие. Получим интерполяционную
формулу Лагранжа:
.
Она правильная, так как степень многочлена
в числителе меньше степени многочлена
стоящего в знаменателе. Мы можем применить
формулу Лагранжа для разложения дроби
на простейшие. Получим интерполяционную
формулу Лагранжа:
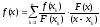 .
.
Пример.
Найти многочлен наименьшей степени по данной таблице его значений:
|
x |
-1 |
0 |
1 |
2 |
3 |
|
y |
6 |
5 |
0 |
3 |
2 |