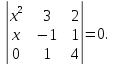Определитель n-го порядка. Свойства определителей. Миноры и алгебраические дополнения. Теорема Лапласа и ее следствие Определитель n-го порядка

Рассмотрим квадратную таблицу А.

А=

Определение. Определителем n-го порядка называется число, полученное из элементов данной таблицы по следующему правилу:

1.Определитель n-го порядка равен алгебраической сумме n! членов.

Каждый член представляет собой произведение n-элементов взятых по одному из каждой строки и каждого столбца таблицы.

2.Член берется со знаком плюс, если перестановки образованные первыми и вторыми индексами элементов 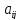, входящие в произведения одинаковой четности (либо обе четные, либо нечетные) и со знаком минус в противоположном случае.

Определитель обозначается символом:

или краткоdet A=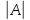.(детерминант А)

Согласно определению =-.

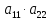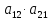Правило вычисления определителя 3ого порядка:

=

.

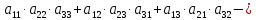
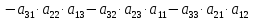Миноры и алгебраические дополнения

Пусть дан определитель n-го порядка (n>1)

Определение 1. Минором элемента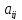определителяn-го порядка называется определитель (n-1)-ого порядка полученный из А вычеркиванием i-й строки и j-го столбца, на пересечении которых стоит данный элемент .

Например:

=

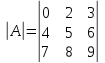
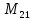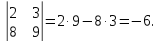
Определение 2. Алгебраическим дополнением элемента 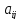называется число

= .

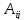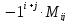Основные свойства определителей n-го порядка

1.О равносильности строк и столбцов.

Величина определителя n-го порядка не меняется, если у него заменить строки соответствующими столбцами.

2.Если у определителей поменять местами две строки (столбца), то определитель изменит знак на противоположный.

3.

= k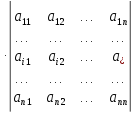

Если все элементы какой-либо строки (или столбца) определителя имеют общий множитель, то этот общий множитель можно вынести за знак определителя.

4.Величина определителя равна нулю, если все элементы какой-либо его строки нули (или столбца).

5.Определитель с двумя пропорциональными строками равен 0.

Например:

6.Величина определителя не изменится, если к его элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

7.Если элементы какой-либо строки i определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, в которых все строки кроме i-й такие же, как в заданном определителе, а i-я строка одного определителя состоит из первых слагаемых, а второго из вторых.

8.Определитель 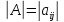равен сумме произведений всех элементов какой-либо его строки на их алгебраические дополнения.

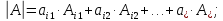
i=1,2,…,n.

=

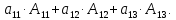
9.Сумма произведений всех элементов какой-либо строки определителя на алгебраические дополнения соответствующих элементов другой строки равна нулю.

Например:

=

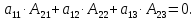
Теорема Лапласа

Теорема. Пусть в определителе d порядка n произвольно выбраны k строк (или k столбцов), 1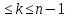.Тогда сумма произведений всех миноровk-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d.

Следствие.  Частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.

Пусть 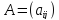— квадратная матрица размера 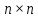. Пусть также задан некоторый номер строки i либо номер столбца j матрицы A. Тогда определитель A может быть вычислен по следующим формулам:

Разложение по i-й строке:

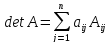
Разложение по j-й строке:

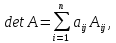
где 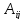  — алгебраическое дополнение к минору, расположенному в строке с номером i и столбце с номером j.

Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить k равным 1 и выбрать -ую строку, тогда минорами, расположенными в этой строке будут сами элементы.

Примеры для самостоятельного решения.

1.Найти х из уравнений и проверить подстановкой корень в определитель.

а)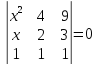; б)

9