3.2. Угловая скорость нмс

Определение: Угловой скоростью вращательного движения НМС вокруг неподвижной оси называется вектор , равный по модулю

, (3.3)

направленный по оси вращения в ту сторону, откуда поворот НМС виден против хода часовой стрелки (рис. 18).

Из определения угловой скорости следует, что

. (3.4)

Размерность модуля угловой скорости в системе СИ:

.

В технике угловая скорость может быть задана по величине через n — число оборотов в секунду или минуту, тогда

, если n об/c, , если n об/мин. (3.5)

3.3. Угловое ускорение нмс

Определение: Угловым ускорением вращательного движения НМС вокруг неподвижной оси называется вектор , равный по модулю

, (3.6)

направленный по оси вращения так, что направления и совпадают в случае ускоренного (знаки совпадают) и противоположны в случае замедленного (знаки не совпадают) вращательного движения НМС вокруг неподвижной оси (рис. 18).

Рис. 18

Из определения углового ускорения следует , что

. (3.7)

Размерность модуля углового ускорения в системе СИ:

.

3.4. Частные случаи вращательного движения нмс вокруг неподвижной оси

3.4.1. Равномерное вращательное движение НМС

В этом случае имеем: .

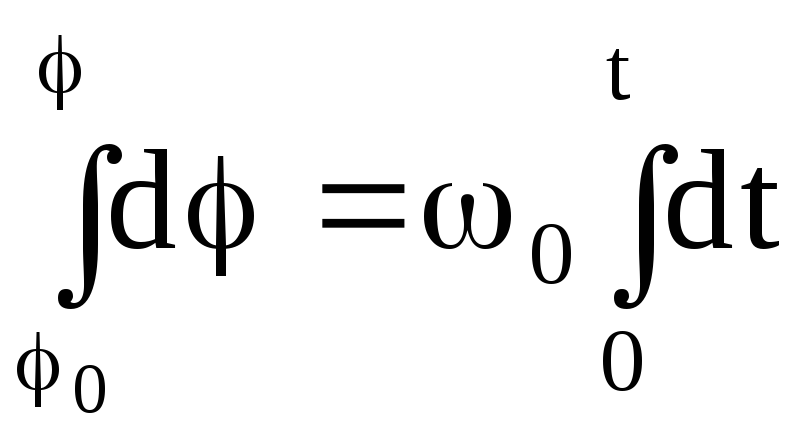На основании формулы (3.3) можно записать: , а, разделив переменные и проинтегрировав , получить:

, (3.8)

где _о и _о здесь и в дальнейшем определяют соответственно угол поворота и модуль угловой скорости НМС при t=0.

Уравнение (3.8) — уравнение равномерного вращательного движения НМС вокруг неподвижной оси.

3.4.2. Равнопеременное вращательное движение НМС

В этом случае имеем: .

На основании формул (3.6) можно записать: , а, разделив переменные и проинтегрировав , получить:

. (3.9)

На основании формул (3.3) можно записать соотношение (3.9) в виде: , а, разделив переменные и проинтегрировав , получить:

. (3.10)

Уравнение (3.10) – уравнение равнопеременного вращательного движения НМС вокруг неподвижной оси, а уравнение (3.9) – уравнение изменения его угловой скорости.

3.5. Траектория, уравнение движения точки НМС

Точки вращающейся НМС, находящиеся на оси вращения, неподвижны, а остальные описывают окружности, плоскости которых перпендикулярны оси вращения, центры лежат на оси, а радиусы равны h — кратчайшему расстоянию от точек до оси вращения.

Так как траектории точек известны, то, используя естественный способ задания движения точки, получим уравнение движения точки вращающейся НМС в виде (рис. 19):

. (3.11)

6. Скорость точки НМС

Используя формулу (1.16) и подставив в нее соотношение (3.11) , получим с учетом (3.3):

, т.е.

. (3.12)

Рассмотрим векторное произведение , используя определение векторного произведения, рис. 19 и формулу (3.12):

 ;

 ;

 векторное произведение составляет правую тройку с векторами и .

Так как на основании (1.15) , то направление совпадает с направлением (рис. 19), следовательно,

. (3.13)

Соотношение (3.13) называется векторной формулой Эйлера.

Рис. 19