
- •Глава 5. Движение нмс с одной неподвижной точкой - сферическое движение нмс
- •5.1. Определение, углы Эйлера, уравнения
- •Движения нмс
- •5.2. Теорема Эйлера-Даламбера
- •5.3. Мгновенная ось вращения, угловая скорость нмс
- •5.4. Выражение угловой скорости нмс через углы Эйлера — кинематические уравнения Эйлера
- •5.5. Угловое ускорение нмс
- •5.6. Скорость точки нмс
- •5.7. Ускорение точки нмс
5.6. Скорость точки нмс
Так как в каждый момент времени движение НМС с одной неподвижной точкой представляет собой мгновенное вращательное движение относительно мгновенной оси, проходящей через эту неподвижную точку, то, используя векторную формулу Эйлера (3.13), для каждого момента времени можно записать:
![]() . (5.7)
. (5.7)
Модуль скорости определяется соотношением:
![]() ,
(5.8)
,
(5.8)
где
![]() rВsin
– кратчайшее расстояние от рассматриваемой
точки до мгновенной оси вращения.
rВsin
– кратчайшее расстояние от рассматриваемой
точки до мгновенной оси вращения.
Направление
скорости
![]() определяется правилом векторного
произведения:
определяется правилом векторного
произведения:
![]() (следовательно, скорость
(следовательно, скорость![]() перпендикулярна также отрезку
перпендикулярна также отрезку![]() );
);
скорость
![]() направлена так, чтобы, глядя с конца
этого вектора, поворот от
направлена так, чтобы, глядя с конца
этого вектора, поворот от![]() был виден против хода часовой стрелки
(рис. 60).
был виден против хода часовой стрелки
(рис. 60).
Скорость
![]() можно проектировать как на неподвижные,
так и на подвижные координатные оси.
можно проектировать как на неподвижные,
так и на подвижные координатные оси.
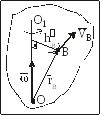
Рис. 60
Представляя выражение (5.7) в виде определителя, получим:
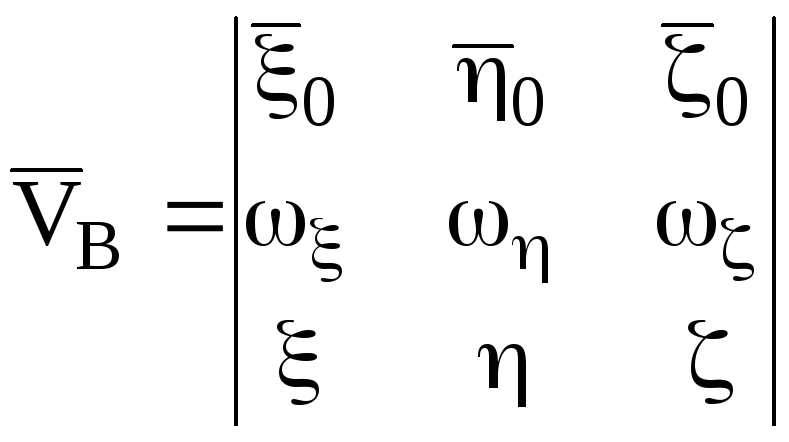 , (5.9)
, (5.9)
где
![]() — координаты точкиB
в неподвижной системе координат, а
— координаты точкиB
в неподвижной системе координат, а
![]() — единичные орты неподвижной системы
координат.
— единичные орты неподвижной системы
координат.
Разлагая
определитель по элементам первой строки,
получим проекции скорости ![]() на неподвижные оси О,
О,
О:
на неподвижные оси О,
О,
О:
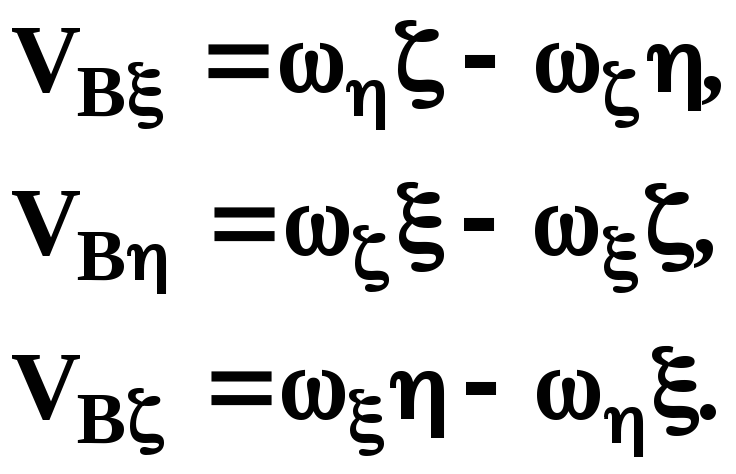 (5.10)
(5.10)
Представляя выражение (5.7) в виде определителя, получим также:
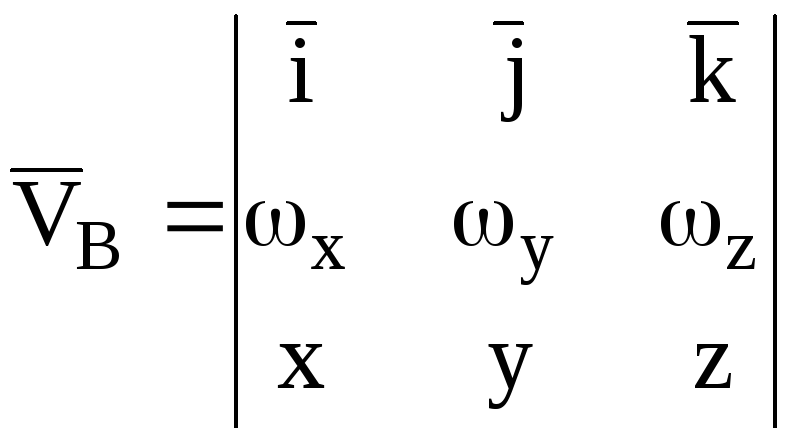 , (5.11)
, (5.11)
где
x, y, z – координаты точки B
в подвижной системе координат, а
![]() – единичные орты подвижной системы
координат.
– единичные орты подвижной системы
координат.
Разлагая
определитель по элементам первой строки,
получим проекции скорости ![]() на подвижные оси
Ох, Оу, Оz:
на подвижные оси
Ох, Оу, Оz:
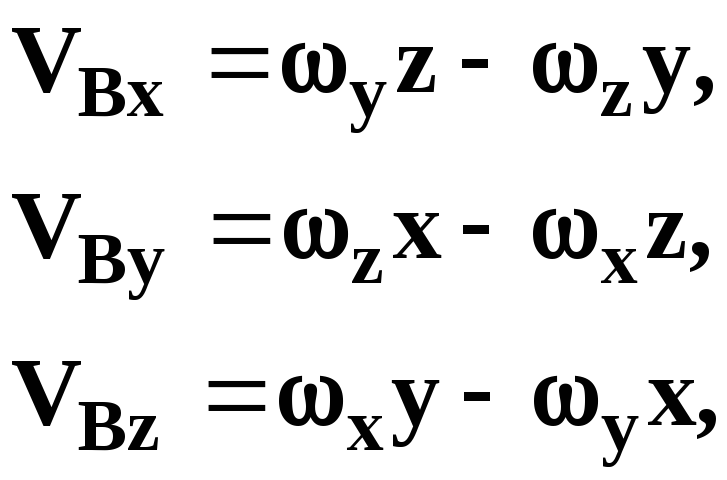 (5.12)
(5.12)
где х, у, z – величины постоянные, так как положение точки относительно осей Охуz, неизменно связанных с движущейся НМС, с течением времени не изменяется.
Формулы (5.10) и (5.12) называются формулами Эйлера.
5.7. Ускорение точки нмс
Ускорение точки В, принадлежащей НМС, имеющую одну неподвижную точку, можно найти, взяв производную по времени от выражения (5.7):
![]()
или
![]() .
(5.13)
.
(5.13)
Первое слагаемое ускорения точки:
![]() (5.14)
(5.14)
называется вращательным ускорением точки.
Величина вращательного ускорения точки определяется формулой:
![]() ,
(5.15)
,
(5.15)
где
![]() = rВ
sin
(рис. 61).
= rВ
sin
(рис. 61).
Направление вращательного ускорения точки определяется правилом векторного произведения:
![]() (следовательно, ускорение
(следовательно, ускорение![]() перпендикулярно также отрезку
перпендикулярно также отрезку![]() );
);
ускорение
![]() направлено так, чтобы, глядя с конца
этого вектора, поворот от
направлено так, чтобы, глядя с конца
этого вектора, поворот от![]() был виден против хода часовой стрелки
(рис. 61).
был виден против хода часовой стрелки
(рис. 61).
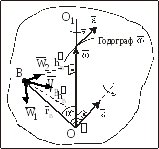
Рис. 61
В
отличие от случая вращения НМС вокруг
неподвижной оси угловое ускорение
![]() при сферическом движении НМС не лежит
на той же прямой, что и угловая скорость
при сферическом движении НМС не лежит
на той же прямой, что и угловая скорость![]() ,
а направлено по касательной к годографу
угловой скорости
,
а направлено по касательной к годографу
угловой скорости![]() .
Поэтому вращательное ускорение
.
Поэтому вращательное ускорение![]() перпендикулярно не к радиусу мгновенного
вращения
перпендикулярно не к радиусу мгновенного
вращения![]() ,
представляющему собой кратчайшее
расстояние от точки до мгновенной оси
вращения, а к отрезку
,
представляющему собой кратчайшее
расстояние от точки до мгновенной оси
вращения, а к отрезку ![]() ,
представляющему собой кратчайшее
расстояние от точки В до прямой, вдоль
которой от точки О отложено угловое
ускорение
,
представляющему собой кратчайшее
расстояние от точки В до прямой, вдоль
которой от точки О отложено угловое
ускорение
![]() (рис. 61).
(рис. 61).
Второе слагаемое ускорения точки:
![]() (5.16)
(5.16)
называется осестремительным ускорением точки.
Величина осестремительного ускорения точки с учетом (5.8) определяется формулой:
![]() .
(5.17)
.
(5.17)
Направление осестремительного ускорения МТ определяется правилом векторного произведения:
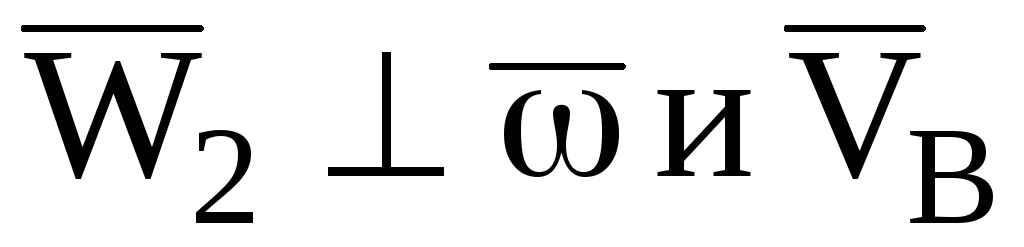 ;
;ускорение
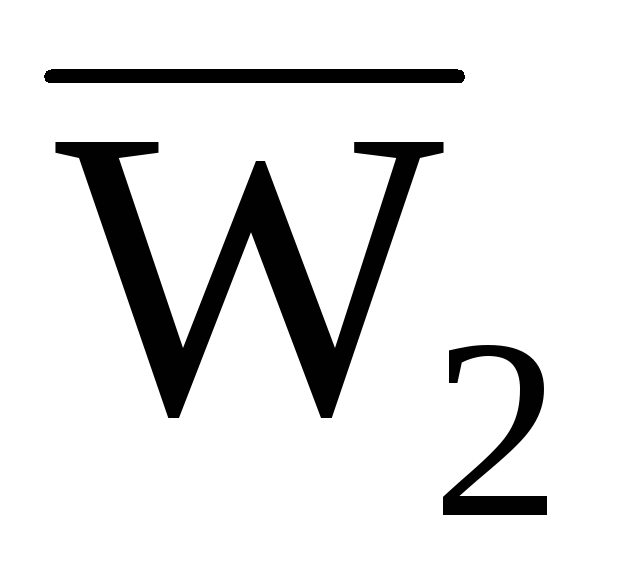 направлено так, чтобы, глядя с конца
этого вектора, поворот от
направлено так, чтобы, глядя с конца
этого вектора, поворот от к
к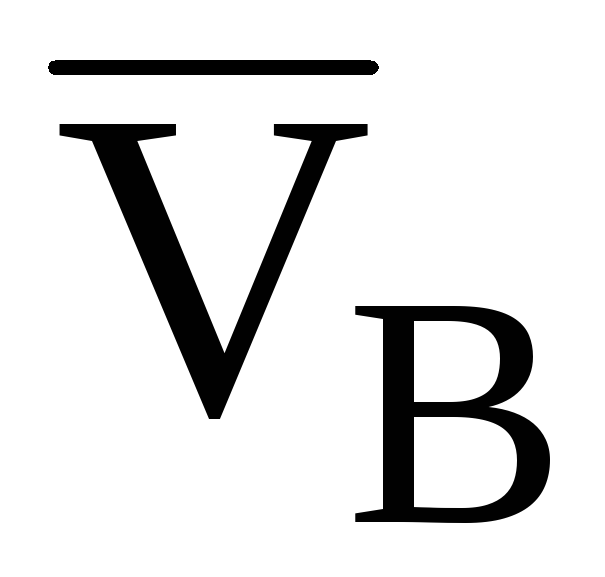 был виден против хода часовой стрелки
(рис. 61).
был виден против хода часовой стрелки
(рис. 61).
Так
как
![]() три взаимно перпендикулярных направления
(рис. 60), то осестремительное ускорение
три взаимно перпендикулярных направления
(рис. 60), то осестремительное ускорение![]() направлено по
направлено по![]() к мгновенной оси вращения (рис. 61).
к мгновенной оси вращения (рис. 61).
Таким образом,
![]() ,
(5.18)
,
(5.18)
а
модуль ускорения
![]() ,
как диагональ параллелограмма,
построенного на ускорениях
,
как диагональ параллелограмма,
построенного на ускорениях![]() и
и![]() ,
может быть определен по формуле:
,
может быть определен по формуле:
![]() . (5.19)
. (5.19)
Подставив соотношения (5.15) и (5.16) в формулу (5.19), получим:
![]() .
.
Ускорение
![]() любой точки НМС с одной неподвижной
точкой можно проектировать как на
неподвижные, так и на подвижные оси
декартовой системы координат.
любой точки НМС с одной неподвижной
точкой можно проектировать как на
неподвижные, так и на подвижные оси
декартовой системы координат.
