8.5.3. Скорость поступательного движения образует с осью вращательного движения нмс произвольный угол
Сложное движение в этом случае состоит из переносного поступательного движения и относительного вращательного движения НМС и представляет собой общий случай движения НМС (глава 6).
Для нахождения
абсолютного движения НМС разложим
вектор
в плоскостиО,
положение которой определяется векторами
и
,
на составляющие, направленные по оси
вращения и перпендикулярно к ней (рис.
87):
Используя случай
8.5.1 для
и
,
получим мгновенное вращательное движение
вокруг мгновенной оси О1z',
параллельной оси Oz и отстоящей от нее
на расстоянии
.
При этом угловая скорость
НМС равна по модулю и направлению данной
угловой скорости
.
Рис. 87
Так как составляющая
скорости поступательного движения НМС
является свободным вектором, то ее можно
перенести параллельно самой себе в
точку О1
и, таким образом, в точке О1
получим случай, рассмотренный в п. 8.5.2,
.
Если НМС участвует
в поступательном движении со скоростью
и во вращательном движении с угловой
скоростью
,
образующей произвольный угол
со скоростью
,
то абсолютное движение НМС будетмгновенным
винтовым движением
со скоростью поступательного движения
и угловой скоростью
,
равной по модулю и направлению данной
угловой скорости
,
с мгновенной винтовой осью, параллельной
оси данного вращения и отстоящей от нее
на расстоянии, равном
.
Теорема:
Совокупность движений НМС, определяемых
мгновенной угловой скоростью
и поступательной скоростью
,
направленной не перпендикулярно к
,
сводится к мгновенному винтовому
движению около мгновенной винтовой
оси.
Сложное движение НМС в этом случае совпадает с общим случаем движения НМС (глава 6) и может быть представлено в виде последовательных мгновенных винтовых движений относительно винтовых осей, положение которых будет непрерывно меняться.
Заключение Алгоритм кинематики – управляющий – к00 упр с комментариями
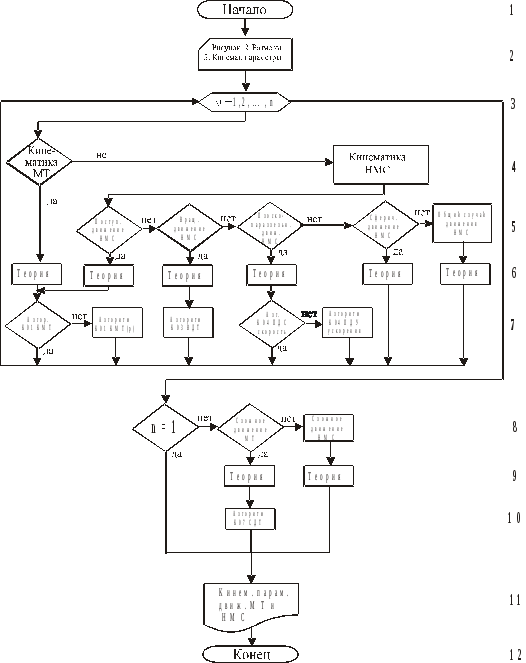
Комментарии
|
К.2. Принимаются рассматриваемые объекты за МТ, СМТ, МС, НМС, АТТ. Определяется подход к рассматриваемому движению как к одному или к нескольким движениям (сложное движение). |
|
К.3,8. Здесь n – число движений МТ и НМС, случай n>1 соответствует сложному движению МТ и НМС. |
|
К.4. Рассматриваются способы задания и кинематические параметры движения МТ. |
|
К.5-7. Определяется тип движения НМС. Поступательное и вращательное движения НМС (главы 2, 3) являются ее простейшими движениями. Плоскопараллельное (глава 4), сферическое (глава 5) и общий случай движения НМС (глава 6) могут быть рассмотрены как одно движение, а могут быть рассмотрены как сложные движения НМС, состоящие из ее простейших движений:
В кинематике НМС:
К6. Следует отметить динамику изменения угловой скорости при различных видах движений:
Т. е. по существу рассмотрены все виды движения НМС, включающие все возможные случаи изменения направления угловой скорости. |
|
К.8-10. Используется при рассмотрении сложного движения МТ (глава 7) один из разделов кинематики НМС (движения подвижной системы координат, связанной с каким-либо НМС, относительно неподвижной системы координат – переносное движение) и кинематики МТ (движение МТ относительно этой НМС – относительное движение). Сложное движение НМС (глава 8) включает в себя различные случаи сочетаний движения НМС. |
и ускорение
(кроме случая поступательного движения
НМС, для которого
и
)
в каждый момент времени одинаковы
для всех МТ, принадлежащих НМС, т. е.
являются кинематическими параметрами
всего НМС;
и ускорения
МТ, принадлежащих НМС зависят от
положения этих МТ в НМС, т. е. являются
кинематическими параметрами этих
МТ.